Основы нейросетевых технологий

2.2. Модель мозга

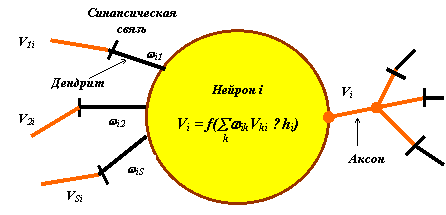
Нейросеть содержит узлы - аналоги нервных клеток - нейронов (рис. 2.7) (нейроподобных элементов, НПЭ) и их соединения - синапсические связи.

Рис. 2.7. Нейрон

Модель нейрона во взаимодействии с другими нейронами нейросети представлена на рис. 2.8.

Рис. 2.8. Модель нейрона

Здесь V_ki - энергетические доли импульсов V_k , выработанных другими нейронами и поступивших на дендриты нейрона i, 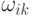- веса дендритов, h_i - пороги. В свою очередь, выработанный импульс V_i также распределяется между дендритами нейронов, с которыми связан нейрон i с помощью ветвящегося аксона. В соответствии с законом распределения энергии, величина V_i делится пропорционально значениям весов дендритов "принимающих" нейронов.

Впрочем, проблему деления (или неделения), лежащую в основе практических моделей, мы еще обсудим далее.

Каждый нейрон или управляем извне, или сети строятся по принципу самоуправления, используя обратные связи. А именно, можно регулировать значения весов синапсических связей 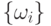и значения порогов h_i . Такое регулирование, во многих вариантах реализованное в разных моделях, и определяет возможность обучения и самообучения сети. Оно задает пути прохождения возбуждений через сеть, простейшим образом формируя связи "посылка - следствие".

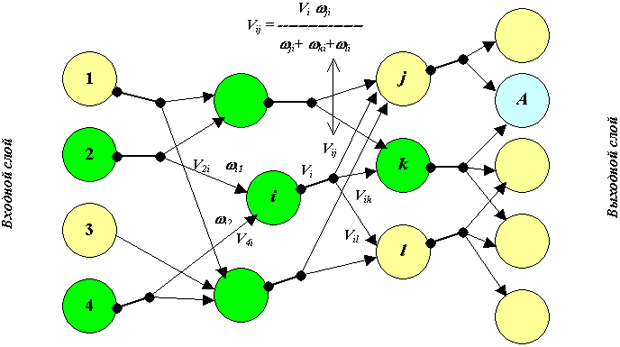
На рис. 2.9 дается фрагмент нейросети, по которому мы можем представить следующее.

увеличить изображение
Рис. 2.9. Нейронная сеть с "правдоподобным" распределением сигнала возбуждения

1. Функции f бывают различны, но просты по объему вычислений. В простейшем случае f cовпадает с линейной формой - указанным аргументом. Т.е. по всем дендритам с учетом их весов (на рис. 2.9) производится суммирование и сравнение с порогом "

   
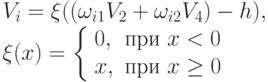
2. Величина превышения порога является величиной возбуждения нейрона или определяет значение величины возбуждения (например, в некоторых моделях величина возбуждения всегда равна единице, а отсутствие возбуждения соответствует нулю). В некоторых моделях допускают и отрицательную величину возбуждения. Значение возбуждения передается через ветвящийся аксон в соответствии со связями данного нейрона с другими нейронами.
3. В общем случае по дендритам может передаваться как возбуждающее, так и тормозящее воздействие. Первое может соответствовать положительному значению веса синапсической связи, второе - отрицательному. Аналогичный эффект достигается при передаче отрицательных значений возбуждения нейронов.
4. В сети распознают входной (рецепторный) слой, воспринимающий внешние возбуждения (например, на который подается видеоизображение), и выходной слой, определяющий результат решения задачи. Работа сети тактируется для имитации прохождения по ней возбуждения и управления им.
5. Существуют два режима работы сети: режим обучения и режим распознавания (рабочий режим).

Установим случайным образом начальные значения весов дендритов всей сети. Пусть нейросеть предназначена для распознавания рукописного текста. Тогда входной слой аналогичен сетчатке глаза, на который ложится изображение. Его подача на входной слой возбуждает в некоторой конфигурации множество нейронов - рецепторов. Пусть мы на входной слой подали и поддерживаем некоторый эталон, например букву А. Через некоторое время возбудится (максимально) нейрон выходного слоя, который мы можем отметить как образ А (прохождение возбуждения отмечено темным цветом). Т.е. его возбужденное состояние мы воспринимаем как ответ "Это буква А ". Введем снова букву А, но с естественными искажениями, обусловленными почерком, дрожанием руки и т.д. Может возбудиться тот же нейрон, но может и другой. Мы же хотим "научить" систему, заставить ее ответить, что это - тоже буква А, т.е. добиться возбуждения того же нейрона выходного слоя.

Тогда по некоторому алгоритму (один из известных алгоритмов называется алгоритм обратного распространения ошибки; в нем воспроизводится подход, используемый в динамическом программировании, здесь мы предлагаем алгоритм "трассировки") мы меняем веса и, возможно, пороги в сети на пути прохождения возбуждения так, чтобы заставить возбудиться нужный нейрон.

Таким способом, предъявляя множество эталонов и регулируя параметры, мы производим обучение сети данному образу. (Математические проблемы несовместимости управления параметрами для разных эталонов оставим в стороне: в живой природе такой процесс проходит успешно, достаточно устойчиво при разумном отличии эталонов. Например, интуитивно ясно, что пытаться заставить один и тот же нейрон выходного слоя возбуждаться и на строчную, и на прописную букву А вряд ли разумно. В лучшем случае он определит, что это буква вообще, а не, скажем, знак пунктуации.)

Обучение заканчивается тогда, когда вероятность "узнавания" достигнет требуемого значения, т.е. необходимость корректировки параметров по предъявляемым эталонам возникает все реже. Теперь можно работать в режиме распознавания - в том ответственном режиме, для которого сеть создавалась. Предъявляем сети различные буквы. Можем быть уверены, что с большой вероятностью, если мы предъявим случайно искаженную и даже зашумленную букву А (конечно, в допустимых пределах), сеть ее распознает, т.е. максимально возбудится соответствующий нейрон выходного слоя.

Можно существенно облегчить обучение, предъявляя эталон "в полном смысле", т.е., например, показывая букву, точно регламентируемую букварем. Тогда предусмотренная (!) степень отклонения от этого эталона, обусловленная почерком, будет влиять на вероятность распознавания этой буквы. Далее мы будем рассчитывать именно на такой способ обучения.

Теперь обобщим "специализацию" входного слоя, связав его с некоторыми характеристиками исходной ситуации (входного вектора), по которой необходимо принимать решение - формировать выходной вектор. Мы учим сеть по эталонным ситуациям, по которым мы знаем решение, а затем в рабочем режиме она выдает нам решение во всем диапазоне ситуаций. При этом она автоматически решает проблему, на какую "знакомую" ей ситуацию более всего похожа введенная ситуация, и, следовательно, какое решение следует выдать. Конечно, с определенной вероятностью правильности.

Такая обработка входной информации при возможном применении в сфере развлечений показана на рис. 2.10 и рис. 2.11.

Отметим, что в экспертных системах требуются точные данные о ситуации, чтобы выдать соответствующее ей заключение. Нейронной сети такой подход "чужд". Она выдает ответ на вопрос "На что похожа данная ситуация?" и, следовательно, какое должно быть заключение. Это еще раз подтверждает, что нейросеть имитирует ассоциативное мышление.

увеличить изображение
Рис. 2.10. Реакция на угрозу

Рис. 2.11. Реакция на поощрение