Приложения ординалов
В большинстве случаев рассуждения с использованием трансфинитной индукции и ординалов можно заменить ссылкой на лемму Цорна; при этом рассуждение становится менее наглядным, но формально более простым. Тем не менее бывают ситуации, когда этого сделать не удается (по крайней мере, неясно, как бы это следовало делать), и приходится пользоваться вполне упорядоченными множествами в явном виде. В этом разделе мы приведем два подобных примера.
Первый из них касается борелевских множеств. (Для простоты мы
рассматриваем подмножества действительной прямой.) Семейство
подмножеств действительной прямой называется  - алгеброй, если
оно замкнуто относительно
конечных и счетных пересечений и объединений, а также
относительно перехода к дополнению. (Это означает, что вместе с
каждым множеством
- алгеброй, если
оно замкнуто относительно
конечных и счетных пересечений и объединений, а также
относительно перехода к дополнению. (Это означает, что вместе с
каждым множеством  это семейство содержит его
дополнение
это семейство содержит его
дополнение 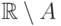 , и вместе с любыми множествами
, и вместе с любыми множествами 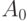 ,
, 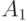 ,
,  семейство содержит их
объединение
семейство содержит их
объединение 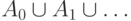 и пересечение
и пересечение 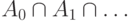 ) Пример:
семейство
) Пример:
семейство  всех подмножеств прямой, очевидно, является
всех подмножеств прямой, очевидно, является  - алгеброй.
- алгеброй.
Теорема 43.Существует минимальная  - алгебра, содержащая
все отрезки
- алгебра, содержащая
все отрезки ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) на прямой.
на прямой.
Доказательство. Формально можно рассуждать так: рассмотрим все
возможные  - алгебры, содержащие отрезки. Их пересечение
будет
- алгебры, содержащие отрезки. Их пересечение
будет  - алгеброй,
и тоже будет содержать все отрезки.
(Вообще пересечение любого семейства
- алгеброй,
и тоже будет содержать все отрезки.
(Вообще пересечение любого семейства  - алгебр будет
- алгебр будет  - алгеброй - это
очевидное
следствие определения.) Эта
- алгеброй - это
очевидное
следствие определения.) Эта  - алгебра и будет
искомой.
- алгебра и будет
искомой.
Множества, входящие в эту минимальную  - алгебру,
называют борелевскими.
- алгебру,
называют борелевскими.
142. Докажите, что всякое открытое и всякое замкнутое подмножество прямой является борелевским. (Указание: открытое множество есть объединение содержащихся в нем отрезков с рациональными концами.)
143. Докажите, что прообраз любого борелевского множества при непрерывном отображении является борелевским множеством.
144. Пусть 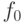 ,
, 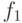 ,
,  -
последовательность непрерывных функций
с действительными аргументами и значениями. Докажите, что множество
точек
-
последовательность непрерывных функций
с действительными аргументами и значениями. Докажите, что множество
точек  , в которых последовательность
, в которых последовательность 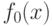 ,
,  ,
,  имеет предел, является борелевским.
имеет предел, является борелевским.
Борелевские множества играют важную роль в дескриптивной теории множеств. Но мы хотим лишь продемонстрировать использование трансфинитной индукции (вряд ли легко заменяемой на использование леммы Цорна) на примере следующей теоремы:
Теорема 44 Семейство всех борелевских множеств имеет мощность континуума.
Доказательство. Класс борелевских множеств можно строить постепенно. Начнем с отрезков и дополнений к отрезкам. На следующем шаге рассмотрим всевозможные счетные пересечения и объединения уже построенных множеств (отрезков и дополнений к ним).
145. Докажите, что при этом получатся (среди прочего) все открытые и все замкнутые подмножества прямой.
Далее можно рассмотреть счетные объединения и пересечения уже построенных множеств и т.д.
Более формально, пусть 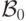 - семейство множеств,
состоящее из всех отрезков и дополнений к ним.
Определим
- семейство множеств,
состоящее из всех отрезков и дополнений к ним.
Определим 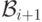 по индукции как семейство множеств, являющихся
счетными объединениями или пересечениями множеств
из
по индукции как семейство множеств, являющихся
счетными объединениями или пересечениями множеств
из 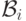 .
.
Все семейства 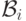 состоят из борелевских множеств
(поскольку счетное объединение или пересечение борелевских
множеств является борелевским). Исчерпывают ли они все
борелевские множества? Вообще говоря, нет: если мы возьмем по
одному множеству из каждого класса
состоят из борелевских множеств
(поскольку счетное объединение или пересечение борелевских
множеств является борелевским). Исчерпывают ли они все
борелевские множества? Вообще говоря, нет: если мы возьмем по
одному множеству из каждого класса 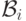 для всех
для всех 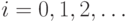 и рассмотрим их
счетное пересечение, то оно вполне может не принадлежать ни
одному из классов. Поэтому мы рассмотрим класс
и рассмотрим их
счетное пересечение, то оно вполне может не принадлежать ни
одному из классов. Поэтому мы рассмотрим класс 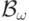 ,
представляющий собой объединение всех
,
представляющий собой объединение всех 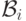 по всем
натуральным
по всем
натуральным  , затем
, затем 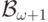 ,
, 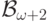 и т.д. Объединение этой последовательности
классов естественно
назвать
и т.д. Объединение этой последовательности
классов естественно
назвать 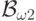 и продолжить построение.
и продолжить построение.
Дадим формальное определение 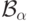 для любого ординала
для любого ординала  . Это делается с
помощью трансфинитной рекурсии. Именно, при
. Это делается с
помощью трансфинитной рекурсии. Именно, при 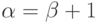 элементами класса
элементами класса 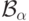 будут счетные объединения и
пересечения множеств из класса
будут счетные объединения и
пересечения множеств из класса 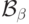 . Если
. Если  -
предельный ординал, отличный от
-
предельный ординал, отличный от  , то
класс
, то
класс 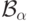 представляет собой объединение всех
представляет собой объединение всех 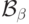 по
всем
по
всем 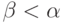 . (Класс
. (Класс 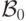 мы уже
определили.)
мы уже
определили.)
Из определения следует, что  при
при  , так что мы получаем
возрастающую цепь классов. Каждый класс замкнут относительно
перехода к дополнению (для начального класса мы об этом
позаботились, далее по индукции). Все классы
, так что мы получаем
возрастающую цепь классов. Каждый класс замкнут относительно
перехода к дополнению (для начального класса мы об этом
позаботились, далее по индукции). Все классы 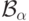 содержатся в классе борелевских множеств, так как мы применяем
лишь операции счетного объединения и пересечения, относительно
которых класс борелевских множеств замкнут.
содержатся в классе борелевских множеств, так как мы применяем
лишь операции счетного объединения и пересечения, относительно
которых класс борелевских множеств замкнут.
Возникает вопрос: как далеко нужно продолжать эту конструкцию? Оказывается, что достаточно дойти до первого несчетного ординала.
Пусть 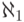 - наименьший
несчетный ординал. (Это - стандартное
для него обозначение.) Другими словами,
- наименьший
несчетный ординал. (Это - стандартное
для него обозначение.) Другими словами, 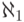 есть семейство
всех
счетных ординалов, упорядоченных отношением
есть семейство
всех
счетных ординалов, упорядоченных отношением  на ординалах.
на ординалах.
