Приложения ординалов

Теорема 46.

(а)Ранг любого дерева (описанного вида) является счетным ординалом.

(б)Всякий счетный ординал является рангом некоторого дерева.

Доказательство. (а) Пусть ранг некоторого дерева, то есть ранг его корня, является несчетным ординалом. Тогда ранг одного из сыновей корня также несчетен. (В самом деле, точная верхняя грань счетного множества счетных ординалов является счетным ординалом; это становится ясным, если рассматривать эти ординалы как начальные отрезки большего - тогда точная верхняя грань будет объединением.) У этого сына в свою очередь есть сын несчетного ранга и т.д. Этот процесс не может оборваться, и мы получаем бесконечную ветвь в противоречии с предположением.

(б) Это утверждение доказывается индукцией: пусть - наименьший счетный ординал, для которого такого дерева нет. Тогда для всех меньших ординалов деревья есть. Возьмем эти деревья и сделаем их поддеревьями с общим корнем (их корни станут сыновьями этого общего корня). Новое дерево также имеет счетное ветвление и ранг его корня равен .

152. Пусть имеется счетное дерево, не имеющее бесконечных ветвей. Предположим, что в каждом его листе находится отрезок или дополнение до отрезка, а в каждой внутренней вершине стоит знак пересечения или объединения. Как сопоставить такому дереву некоторое борелевское множество? (Указание: покажите, что в каждой вершине можно единственным образом написать некоторое множество, согласованное с пометками.) Покажите, что все борелевские множества могут быть получены таким способом.

Деревья с пометками, рассмотренные в этой задаче, представляют собой как бы бесконечные формулы, составленные из отрезков и дополнений к ним с помощью операций счетного объединения и пересечения (конечные деревья соответствовали бы конечным формулам). Можно условно сказать, что борелевские множества - это множества, выражающиеся с помощью таких формул.

153.Докажите, что семейство борелевских множеств имеет мощность континнума, используя " бесконечные формулы" - размеченные деревья, в которых нет бесконечных ветвей. (Это доказательство обходится без ординалов, трансфинитной индукции и даже леммы Цорна - хотя и использует аксиому выбора.)

В заключение приведем скорее забавный, чем важный, пример использования трансфинитной рекурсии и ординалов.

Теорема 47. Существует множество точек на плоскости, которое пересекается с каждой прямой ровно в двух точках.

Две параллельные прямые почти что удовлетворяют этому требованию (исключением являются лишь параллельные им прямые). Но избавиться от этого исключения не так просто.

Доказательство. Требования к множеству можно сформулировать так: никакие три точки не лежат на одной прямой, но любая прямая пересекает его не менее чем в двух точках.

Будем строить это множество трансфинитной рекурсией. Пусть - минимальный ординал, имеющий мощность континуума. (Если континуум - гипотеза верна, то он совпадает с 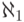, но это нам не важно.) Тогда множество всех меньших ординалов можно поставить во взаимно однозначное соответствие с множеством всех прямых на плоскости. Пусть - прямая, соответствующая ординалу .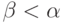

Для каждого 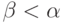построим множество 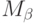, в котором никакие три точки не лежат на одной прямой, следующим образом. Объединим все построенные ранее множества 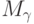при всех 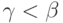. Могут ли в этом множестве (обозначим его ) какие - то три точки лежать на одной прямой? Если да, то эти точки берутся из каких-то множеств 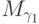, , 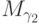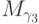; возьмем наибольший из ординалов 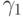, , 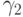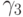; в соответствующем множестве будут три точки, лежащие на одной прямой, что противоречит предположению индукции.

Посмотрим, во скольких точках пересекает прямая множество . Таких точек (по доказанному) не больше двух. Если их ровно две, то все хорошо и мы новых точек не добавляем, считая, что 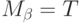. Если их меньше, то мы должны добавить новые точки (до двух), но только так, чтобы при этом не образовалось трех точек, лежащих на одной прямой. Другими словами, нельзя добавлять точки, которые лежат на пересечении с прямыми, проходящими через пары уже имеющихся точек.

Сколько таких прямых (то есть сколько пар уже имеющихся точек)? По построению видно, что все уже имеющиеся точки лежат по две на каждой прямо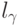й при 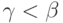. (Строго говоря, это следует включить в индуктивное предположение.) Таким образом, множество по мощности есть , а пар точек не больше 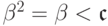. Поэтому запрещенные точки составляют лишь малую (по мощности) часть прямой , и можно выбрать две разрешенные точки.

Теперь осталось объединить множества 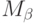для всех ординалов 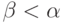и получить искомое множество. (По условию три точки на одной прямой в нем появиться не могут, а всякая прямая будет рано или поздно рассмотрена и две точки на ней будут обеспечены.)

154. Найдите ошибку в следующем " опровержении гипотезы континуума": пусть . Упорядочим отрезок по типу 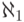. Рассмотрим функцию двух переменных, равную единице на паре 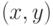, если 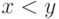(в смысле этого порядка), и нулю в остальных случаях. Тогда при фиксированном функия 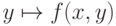равна единице везде, кроме счетного множества, и потому интегрируема и 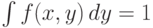при любом . С другой стороны, функция 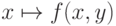равна нулю всюду, кроме счетного множества, так что . 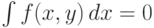Получаем противоречие с теоремой Фубини, которая утверждает, что