Введение в математическое программирование
[+]
Донецкий национальный технический университет
Опубликован: 09.07.2007 | Доступ: свободный | Студентов: 3115 / 710 | Оценка: 4.34 / 4.12 | Длительность: 13:54:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Программист
Теги: beta, анализ, базисное решение, вычисления, двойственная задача, задача линейного программирования, законы, искусственная жизнь, исследования, метод полного исключения, моделирование, нелинейное программирование, оптимальный план, поиск, программирование, симплекс, симплекс-метод, функция лагранжа, экстремум функции, электронная почта, элементы

Лекция 5: Двойственность в линейном программировании. Нахождение допустимых базисных решений. Двойственная задача линейного программирования, ее структура и свойства. Общий случай двойственности.

A
|
версия для печати
< Лекция 4 || Лекция 5: 1234 || Лекция 6 >
2.2. Общий случай двойственности

В предыдущем разделе были установлены основные соотношения для пары двойственных задач ЛП при ограничениях в форме неравенств. Обобщим эти результаты на случай произвольных ограничений.

Пусть прямая задача ЛП задана в виде

\text{максимизировать} \; \sum_{j=1}^n c_j x_j ( 2.2.1)
при условиях
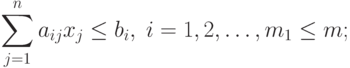\sum_{j=1}^n a_{ij} x_j \leq b_i , \; i=1,2,\ldots,m_1 \leq m ; ( 2.2.2)
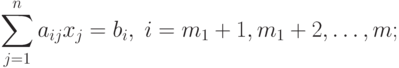\sum_{j=1}^n a_{ij} x_j = b_i , \; i = m_1 + 1, m_1 + 2, \ldots, m ; ( 2.2.3)
x_j \geq 0, \; j = 1,2,\ldots,n_1 \leq n.

Тогда двойственная задача по отношению к задаче (2.2.1)-(2.2.3) записывается так:

\text{минимизировать} \; \sum_{i=1}^m b_i y_i ( 2.2.4)
при условиях
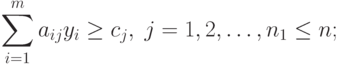\sum_{i=1}^m a_{ij} y_i \geq c_j, \; j = 1,2,\ldots, n_1 \leq n ; ( 2.2.5)
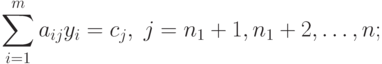\sum_{i=1}^m a_{ij} y_i = c_j, \; j = n_1+1,n_1+2,\ldots, n ; ( 2.2.6)

Таким образом, задача, двойственная к задаче со смешанными ограничениями (неравенства-равенства), составляется согласно следующим правилам.

  1. Если переменная xj прямой задачи предполагается неотрицательной, то j -е условие системы (2.2.5) является неравенством.
  2. Если на переменную xj не накладывается ограничение на знак, то j -е ограничение двойственной задачи (2.2.5) будет равенством.

Аналогично связаны знаки переменных двойственной задачи yi и соответствующие им ограничения прямой задачи.

Заметим, что если положить m1=m и n1=n, то получим частный случай пары двойственных задач с ограничениями в форме неравенств.

Докажем справедливость соотношений (2.2.1) - (2.2.3) и (2.2.4) - (2.2.6), связывающих прямую и двойственную задачи.

Свяжем с каждой ЛП - задачей вида (2.2.1) - (2.2.3) следующую задачу с ограничениями в форме неравенств:

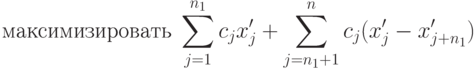\text{максимизировать} \; \sum_{j=1}^{n_1} c_j x'_j + \sum_{j=n_1 +1}^n c_j (x'_j - x'_{j+n_1}) ( 2.2.7)
при условиях
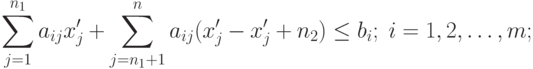\sum_{j=1}^{n_1} a_{ij} x'_j + \sum_{j=n_1 + 1}^n a_{ij} (x'_j - x'_j+n_2) \leq b_i; \; i=1,2,\ldots,m ; ( 2.2.8)
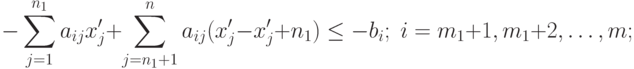- \sum_{j=1}^{n_1} a_{ij} x'_j + \sum_{j=n_1 + 1}^n a_{ij} (x'_j - x'_j+n_1) \leq -b_i; \; i=m_1+1,m_1+2,\ldots,m ; ( 2.2.9)
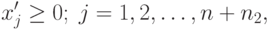x'_j \geq 0; \; j=1,2,\ldots,n+n_2, ( 2.2.10)
где n2=n-n1 - число переменных задачи (2.2.1) - (2.2.3), на которые не наложено условие неотрицательности.

Установим соответствие между переменными задач (2.2.1) - (2.2.3) и (2.2.7) - (2.2.10). Сравнивая формы их записи, убеждаемся, что n -мерный вектор х={x1,.,xn} и (n+n2) -мерный вектор 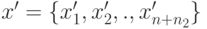x' = \{ x'_1, x'_2, .,x'_{n+n_2} \} связаны соотношением

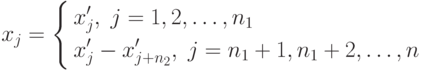x_j = \left\{ \begin{aligned} & x'_j, \; j=1,2,\ldots,n_1 \\ & x'_j - x'_{j+n_2}, \; j=n_1 + 1, n_1 + 2, \ldots, n \end{aligned} \right. ( 2.2.11)

Очевидно, каждому (n+n2) -мерному вектору x' соответствует единственный n -мерный вектор x, и вместе с тем произвольному n -мерному вектору x соответствует целое семейство (n+n2) -мерных векторов х'.

Таким образом, соответствие, устанавливаемое формулой (2.2.11), является однозначным только в одну сторону.

Вместе с тем среди семейства векторов х', соответствующих x, всегда существуют векторы с неотрицательными компонентами.

Пусть вектор 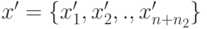x'= \{ x'_1, x'_2, ., x'_{n+n_2} \} - план задачи (2.2.7) -(2.2.10). Используя соотношение (2.2.11), можно легко получить, что соответствующий вектор x является планом задачи. И наоборот, если x - план задачи (2.2.1) - (2.2.3), то существует целое семейство планов x' задачи (2.4.38) - (2.4.41), среди которых имеются заведомо неотрицательные.

Одним из них является вектор 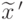{\widetilde{x}}\,' где

j = 1, 2, ., n1,
j = n1+1, n1+2, ., n,
j = n+1, n+2, ., n+n2.

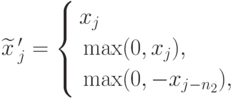{\widetilde{x}}\,'_j = \left\{ \begin{aligned} & x_j \\ & \max (0, x_j) , \\ & \max (0, -x_{j-n_2}) , \end{aligned} \right. ( 2.2.12)

Неотрицательность всех компонентов 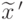{\widetilde{x}}\,' очевидна, а соответствие векторов x и 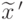{\widetilde{x}}\,' следует из равенства

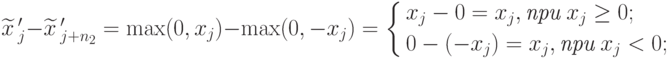
{\widetilde{x}}\,'_j - {\widetilde{x}}\,'_{j+n_2} = \max (0, x_j) - \max (0, -x_j) = \left\{ \begin{aligned} & x_j - 0 = x_j, \textit{при} \; x_j \geq 0; \\ & 0 - (-x_j) = x_j , \textit{при} \; x_j < 0; \end{aligned} \right.
где j=n1+1; n1+2,.,n...

Рассмотрим задачу (2.2.4) - (2.2.6), двойственную к задаче (2.2.1) - (2.2.3). Нетрудно показать, что она приводится к виду (2.2.1) - (2.2.3). Для этого достаточно положить 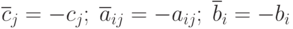\overline{c}_j = -c_j ; \; \overline{a}_{ij} = -a_{ij} ; \; \overline{b}_i = -b_i. При этом задача (2.2.4) - (2.2.6) переходит в задачу

\text{минимизировать} \; \sum_{i=1}^m \overline{b}_i y_i ( 2.2.13)
при условиях
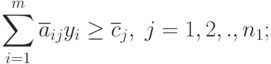\sum_{i=1}^m \overline{a}_{ij} y_i \geq \overline{c}_j, \; j=1,2,.,n_1 ; ( 2.2.14)
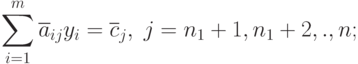\sum_{i=1}^m \overline{a}_{ij} y_i = \overline{c}_j, \; j=n_1+1, n_1+2,.,n ; ( 2.2.15)
y_i \ge 0; \; i=1,2,.,m_1. ( 2.2.16)

Поэтому задаче (2.2.4) - (2.2.6) соответствует следующая задача с ограничениями в форме неравенств:

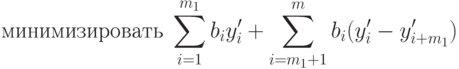\text{минимизировать} \; \sum_{i=1}^{m_1} b_i y'_i + \sum_{i=m_1 + 1}^m b_i (y'_i - y'_{i+m_1}) ( 2.2.17)
при условиях
\sum^m_{i=1} \overline b_{ij}y_{ij}\ge \overline c_j \ j= 1,2 \ldots,n; ( 2.2.18)
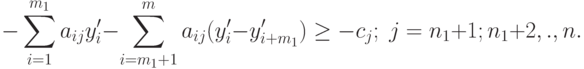- \sum_{i=1}^{m_1} a_{ij} y'_i - \sum_{i=m_1+1}^m a_{ij}(y'_i - y'_{i+m_1}) \geq -c_j ; \; j=n_1+1; n_1+2,.,n. ( 2.2.19)
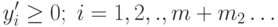y'_i \geq 0; \; i=1,2,.,m+m_2 \ldots ( 2.2.20)
где m2 = m - m1 - число переменных yi, на которые не наложено условие неотрицательности.

Вектор y={y1,.,ym} и соответствующий ему (m+m2) мерный вектор 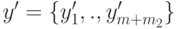y' = \{ y'_1,.,y'_{m+m_2} \} связанны соотношением

y_i = \left \{ \begin{aligned} & y'_i, \; i=1,2,\ldots,m_1 ; \\ & y'_i - y'_{i+m_1}, \; i=m_1 +1, m_1+2,\ldots,m. \end{aligned} \right. ( 2.2.21)

Следовательно, каждому плану y' задачи (2.2.17) - (2.2.20) соответствует план у задачи (2.2.4) - (2.2.6), и наоборот: любой неотрицательный вектор, соответствующий плану (решению) задачи (2.2.4) - (2.2.6), является решением задачи (2.2.18) - (2.2.20). При этом, если у' и у - два соответствующих друг другу решения, то из оптимальности одного из них непосредственно следует оптимальность другого.

Запишем задачу, двойственную к (2.2.7) - (2.2.10). Непосредственной проверкой можно убедиться в том, что получим задачу в форме (2.2.17) - (2.2.20). Таким образом, задачи (2.2.7) - (2.2.10) и (2.2.17) -(2.2.20) с произвольными ограничениями (неравенства - равенства) также представляют собой двойственную пару.

Заметим, что все теоремы двойственности, доказанные для задач с ограничениями в форме неравенств, легко распространяются на общий случай задач с произвольными ограничениями.

Рассмотрим для примера теорему 2.2.1.

Если х и у - допустимые решения прямой (2.2.1) - (2.2.2) и двойственной (2.2.4) - (2.2.6) задачи и если при этом 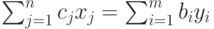\sum_{j=1}^n c_j x_j = \sum_{i=1}^m b_i y_i, то х и у - оптимальные решения этих задач.

Доказательство. Допустим, что задача (2.2.1) - (2.2.2) разрешима и x -ее допустимое решение, а у - допустимое решение (план) задачи (2.2.4) - (2.2.6). Рассмотрим вектор 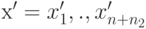х'={x'_1,.,x'_{n+n_2}}, связанный с вектором х соотношениями (2.2.11), с неотрицательными компонентами. По доказанному выше х' является решением задачи (2.2.7).

Воспользуемся тогда теоремой 2.2.1 для задач с ограничениями - неравенствами.

Согласно этой теореме, если х' и у' - допустимые решения пары двойственных задач и выполняется равенство

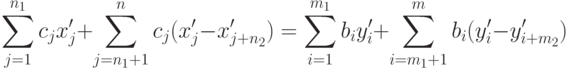\sum_{j=1}^{n_1} c_j x'_j + \sum_{j=n_1+1}^n c_j (x'_j - x'_{j+n_2}) = \sum_{i=1}^{m_1} b_i y'_i + \sum_{i=m_1+1}^m b_i (y'_i - y'_{i+m_2}) ( 2.2.22)

то х' и у' - оптимальные решения этой пары задач.

Используя соотношения (2.2.11), (2.2.21), связывающие соответствующие планы х' и х, у и у', получим

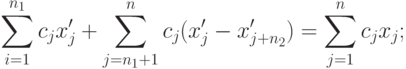\sum_{i=1}^{n_1} c_j x'_j + \sum_{j=n_1+1}^n c_j (x'_j - x'_{j+n_2}) = \sum_{j=1}^{n} c_j x_j ; ( 2.2.23)

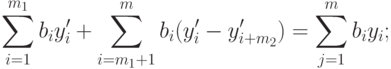\sum_{i=1}^{m_1} b_i y'_i + \sum_{i=m_1+1}^m b_i (y'_i - y'_{i+m_2}) = \sum_{j=1}^{m} b_i y_i ; ( 2.2.24)

Таким образом, соотношения (2.2.22) и (2.2.23) - (2.2.24) - эквивалентны, поэтому планы х' и у' - оптимальны.

Но по доказанному выше каждому оптимальному х' соответствует единственный оптимальный план х, а каждому оптимальному плану у' соответствует единственный план у. Теорема доказана.

Аналогичным образом могут быть доказаны остальные теоремы двойственности для произвольных ограничений.

Дальше >>
< Лекция 4 || Лекция 5: 1234 || Лекция 6 >

Вопросы и ответы

вопросов: 0