Лекция 5: Двойственность в линейном программировании. Нахождение допустимых базисных решений. Двойственная задача линейного программирования, ее структура и свойства. Общий случай двойственности.
2. Двойственная задача линейного программирования
2.1. Структура и свойства двойственной задачи
Задачу максимизации ЛП с экономической точки зрения можно рассматривать как задачу о распределении ограниченных ресурсов b1,.,bm между различными потребителями, например между определенными технологическими процессами, которые представляются столбцами A1,.,An матрицы ограничений задачи.
Любое допустимое решение задачи ЛП x1,.,xn дает конкретное распределение, которое указывает ту долю каждого из ресурсов, которая должна быть использована при осуществлении соответствующего технологического процесса.
Рассмотрим пример. Предприятие производит три вида продукции x1, x2 и x3, каждый из которых проходит обработку на токарном, фрезеровальном и сверлильном станках. Общий фонд машинного времени для каждого из станков ограничен. Пусть c1, c2 и c3 - прибыль от реализации единицы соответствующего вида продукции. Необходимо определить, какое количество продукции каждого вида следует производить каждую неделю, чтобы обеспечить максимальную прибыль.
Эта задача имеет такой вид:
 |
( 2.1.1) |
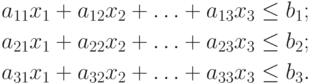 |
( 2.1.2) |
Обозначим через y1, y2, y3 - цену единицы времени работы токарного, сверлильного и фрезеровального оборудования.
Тогда a11y1 + a21y2 + a31y3 можно трактовать как затраты на изготовление единицы продукции первого вида;
Предположим, что цены ресурсов y1, y2, y3 выбраны так, что выполняются соотношения
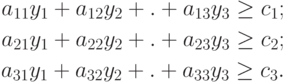 |
( 2.1.3.) |
Поскольку b1, b2, b3 - общий использованный ресурс машинного времени для каждого из станков, то b1y1+b2y2+b3y3 - общие затраты на производство (общая стоимость использованных ресурсов).
Тогда можно сформулировать следующую задачу.
Требуется определить цены y1, y2, y3, удовлетворяющие условиям (2.1.3), при которых минимизируются суммарные затраты на производство, а именно:
 |
( 2.1.4.) |

Задачу (2.1.3), (2.1.4) называют двойственной относительно задачи (2.1.1), называемой прямой.
Запишем прямую и двойственную задачи в общем виде.
Прямая задача:
 |
( 2.1.5.) |
 |
( 2.1.6.) |
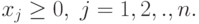 |
( 2.1.7.) |
 |
( 2.1.8.) |
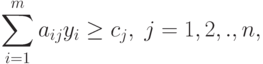 |
( 2.1.9.) |
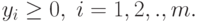 |
( 2.1.10.) |
В матричном виде пара двойственных задач записывается следующим образом:
Прямая задача:
 |
( 2.1.11.) |
 |
( 2.1.12.) |
 |
( 2.1.13.) |
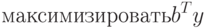 |
( 2.1.14.) |
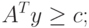 |
( 2.1.15.) |
 |
( 2.1.16.) |
Сопоставляя формы записи прямой и двойственной задач, можно установить между ними следующие взаимосвязи.
- Если прямая задача является задачей максимизации, то двойственная будет задачей минимизации, и наоборот.
- Коэффициенты целевой функции прямой задачи c1,...,cn становятся свободными членами ограничений двойственной задачи.
- Свободные члены ограничений прямой задачи b1,...,bm становятся коэффициентами целевой функции двойственной задачи.
- Матрица ограничений двойственной задачи получается путем транспонирования матрицы ограничений прямой задачи.
- Знаки неравенств в ограничениях изменяются на противоположные.
- Число ограничений прямой задачи равно числу переменных двойственной задачи, и наоборот.
