Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Донецкий национальный технический университет

Опубликован: 09.07.2007 | Доступ: свободный | Студентов: 3119 / 713 | Оценка: 4.34 / 4.12 | Длительность: 13:54:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист

|

Вам нравится? Нравится 52 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Лекция 5: Двойственность в линейном программировании. Нахождение допустимых базисных решений. Двойственная задача линейного программирования, ее структура и свойства. Общий случай двойственности.

A

|

версия для печати

Переменные y₁,...,y_m двойственной задачи иногда называют теневыми ценами.

Двойственную задачу выгоднее решать, чем прямую, если в прямой задаче при малом количестве переменных имеется большое количество ограничений (m > n).

Связь между оптимальными решениями прямой и двойственной задач устанавливают, анализируя следующие теоремы теории двойственности.

Теорема 2.1.1. Если x₀ и y₀ допустимые решения прямой и двойственной задач, то есть 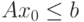$Ax_0 \leq b$ и $A^T y_0 \geq c$ , то

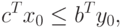$c^T x_0 \leq b^T y_0,$

( 2.1.17)

то есть значения целевой функции прямой задачи никогда не превышают значения целевой функции двойственной задачи.

Доказательство. Умножим выражение (2.1.12) на 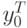y_0^T , получим

$y_0^T Ax_0 \leq y_0^T b.$

( 2.1.18)

Аналогично умножим (2.1.15) на 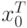x_0^T :

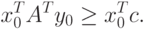$x_0^T A^T y_0 \geq x_0^T c.$

( 2.1.19)

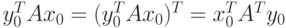Но y_0^T Ax_0 = (y_0^T Ax_0)^T = x_0^T A^T y_0 , а кроме того x_0^T c = c^T x_0 .

Поэтому, сравнивая (2.1.19) и (2.1.18), получим

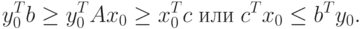
$y_0^T b \geq y_0^T Ax_0 \geq x_0^T c \; \text{или} \; c^T x_ 0 \leq b^T y_0.$

Теорема доказана.

Теорема 2.1.2. (основная теорема двойственности). Если x₀ и y₀ допустимые решения прямой и двойственной задач и кроме того, если c^Tx₀=b^Ty₀, то x₀ и y₀ - оптимальные решения пары двойственных задач.

Доказательство. Согласно теореме 2.1.1 для всех допустимых решений х и у справедливо неравенство (2.1.17). В частности, для всех допустимых решений х справедливо 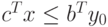$c^T x \leq b^T y_0$ . Однако из условия теоремы c^Tx=b^Ty₀ следует $c^T x \leq c^T x_0$ . Следовательно, x₀ - оптимальное решение.

Вторая часть теоремы доказывается аналогично.

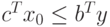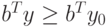В силу теоремы 2.1.1 для всех допустимых у справедливо $c^T x_0 \leq b^T y$ . Но из условия c^T x_0=b^T y_0 следует, что $b^T y \geq b^T y_0$ для всех $y \geq 0$ . Таким образом, y₀ - оптимальное решение.

Теорема 2.1.3. Если в оптимальном решении прямой задачи (2.1.5) - (2.1.7) i - тое ограничение выполняется как строгое неравенство, то оптимальное значение соответствующей двойственной переменной равно нулю, то есть

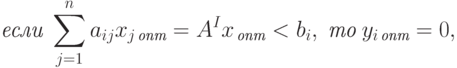$\textit{если} \; \sum_{j=1}^n a_{ij} x_{j \, \textit{опт}} = A^I x_{\, \textit{опт}} < b_i, \; \textit{то} \; y_{i \, \textit{опт}} = 0,$

( 2.1.20)

где A_i - i -я строка матрицы А.

Смысл теоремы 2.1.3 состоит в слeдующем. Если некоторый ресурс b_i имеется в избытке, и і -тое ограничение при оптимальном решении выполняется как строгое неравенство, то это ограничение становится несущественным, и оптимальная цена соответствующего ресурса равна нулю.

Теорему 2.1.3. дополняет теорема 2.1.4, устанавливающая взаимосвязь между оптимальным решением прямой задачи и ограничениями двойственной.

Теорема 2.1.4. Если в оптимальном решении двойственной задачи ограничение j выполняется как строгое неравенство, то оптимальное значение соответствующей переменной прямой задачи должно быть равно нулю, то есть

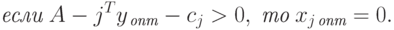$\textit{если} \; A-j^T y_{\, \textit{опт}} - c_j > 0, \; \textit{то} \; x_{j \, \textit{опт}} =0.$

( 2.1.21)

Дадим экономическую интерпретацию теоремы 2.1.4.

Поскольку величины y_i (i=1,2,.,m) представляют собой цены соответствующих ресурсов, то $A^T_j y = \sum_{i=1}^n a_{ij} y_i$ - это затраты на j -й технологический процесс, а величина c_j - прибыль от реализации единицы соответствующего продукта. Поэтому с экономической точки зрения теорема 2.1.4 означает следующее: если j -й технологический процесс оказывается строго невыгодным относительно оптимальных цен ресурсов y_опт, то в оптимальном решении прямой задачи интенсивность использования данного технологического процесса должна быть равна нулю, и соответствующий вид продукции не выпускается как нерентабельный.

Таким образом, теорема 2.1.4 выражает принцип рентабельности для оптимально организованного производства.

Из этой теоремы вытекает также, что если $x_{j \, \textit{опт}} > 0$ , то

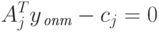$A_j^T y_{\, \textit{опт}} - c_j = 0$

( 2.1.22)

Предположим, что среди переменных x₁, x₂, ., x_n прямой задачи есть множество из m переменных, которые в оптимальном решении прямой задачи имеют ненулевые значения. Пусть, например, такими переменными оказались первые по порядку m переменных.

Тогда на основании уравнения (2.1.22) получаем m условий рентабельности:

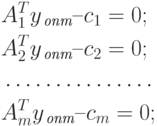$\begin{align*} & A^T_1 y_{\, \textit{опт}} – c_1 =0; \\ & A^T_2 y_{\, \textit{опт}} – c_2 =0; \\ & \ldots \ldots \ldots \ldots \ldots \\ & A^T_m y_{\, \textit{опт}} – c_m =0; \end{align*}$

( 2.1.23)

где

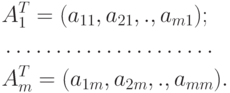
$\begin{align*} & A^T_1 = (a_{11}, a_{21}, . , a_{m1}); \\ & \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\ & A^T_m = (a_{1m}, a_{2m}, . , a_{mm}). \end{align*}$

Доказательства теорем 2.1.3 и 2.1.4 проведем последовательно.

Пусть х_опт и y_опт - оптимальные решения прямой и двойственной задач. Поскольку эти решения допустимые, то

$Ax_{\, \textit{опт}} - b \leq 0;$

( 2.1.24)

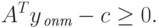$A^T y_{\, \textit{опт}} - c \geq 0.$

( 2.1.25)

Умножив неравенство (2.1.24) на 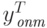$y^T_{\, \textit{опт}}$ , а неравенство (2.1.25) - на $х^T_{\, \textit{опт}}$ , получим

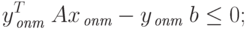$y^T_{\, \textit{опт}} \; Ax_{\, \textit{опт}} - y_{\, \textit{опт}} \; b \leq 0;$

( 2.1.26)

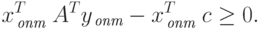$x^T_{\, \textit{опт}} \; A^T y_{\, \textit{опт}} - x^T_{\, \textit{опт}} \; c \geq 0.$

( 2.1.27)

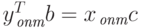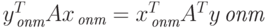Так как в силу теоремы 2.2 $y^T_{\, \textit{опт}} b = x_{\, \textit{опт}} c$ и $y^T_{\, \textit{опт}} Ax_{\, \textit{опт}} = x^T_{\, \textit{опт}} A^T y{\, \textit{опт}}$ , то выражения (2.1.26), (2.1.27) строго равны нулю.

Расписав левую часть неравенства (2.1.26), получим

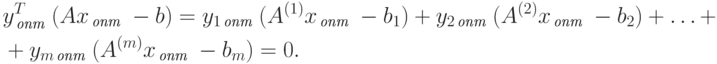$\begin{align*} & y^T_{\, \textit{опт}} \; (Ax_{\, \textit{опт}} \; - b) = y_{1 \, \textit{опт}} \; (A^{(1)} x_{\, \textit{опт}} \; - b_1) + y_{2 \, \textit{опт}} \; (A^{(2)} x_{\, \textit{опт}} \; - b_2) + \ldots + \\ & +y_{m \, \textit{опт}} \; (A^{(m)} x_{\, \textit{опт}} \; - b_m) = 0 . \end{align*}$

( 2.1.28)

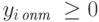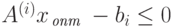Поскольку $y_{i \, \textit{опт}} \; \geq 0$ и $A^{(i)} x_{\, \textit{опт}} \; - b_i \leq 0$ для всех i = 1, 2, ..., m, то левая часть уравнения (2.1.28) может быть равна 0 только в том случае, если каждое слагаемое в отдельности равно нулю.

Таким образом, для каждого i, при котором 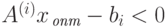$A^{(i)} x_{\, \textit{опт}} - b_i < 0$ , имеем 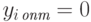$y_{i \, \textit{опт}} = 0$ , что и требовалось доказать в теореме 2.1.3.

Рассмотрим теперь левую часть неравенства (2.1.27), предварительно расписав ее

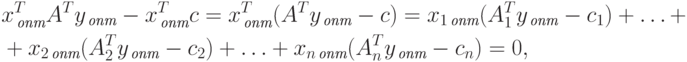$\begin{align*} & x^T_{\, \textit{опт}} A^T y_{\, \textit{опт}} - x^T_{\, \textit{опт}} c = x^T_{\, \textit{опт}} (A^T y_{\, \textit{опт}} - c) = x_{1 \, \textit{опт}} (A^T_1 y_{\, \textit{опт}} - c_1) + \ldots + \\ & + x_{2 \, \textit{опт}} (A^T_2 y_{\, \textit{опт}} - c_2) + \ldots + x_{n \, \textit{опт}} (A^T_n y_{\, \textit{опт}} - c_n) = 0, \end{align*}$

( 2.1.29)

где A=[A₁,A₂,...,A_n].

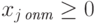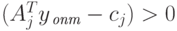Так как все $x_{j \, \textit{опт}} \geq 0$ и $A_j^T y_{\, \textit{опт}} - c_j \geq 0$ для всех j=1,.,n, то уравнение (2.1.29) строго равно нулю, если для каждого j, при котором $(A_j^T y_{\, \textit{опт}} -c_j) > 0$ , соответствующая переменная $x_{j \, \textit{опт}}$ равна нулю.

Приведем еще две важные теоремы теории двойственности.

Теорема 2.1.5. ( теорема существования ). Прямая и двойственная задачи имеют оптимальные решения тогда и только тогда, когда обе они имеют допустимые решения.

Теорема 2.1.6. (теорема двойственности). Допустимый вектор x₀ оптимальный тогда и только тогда, когда в двойственной задаче имеется такое допустимое решение y₀, что

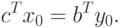( 2.1.30)

Между оптимальными решениями прямой и двойственной задач и элементами индексных строк симплекс-таблиц, соответствующих этим решениям, существует следующая взаимосвязь:

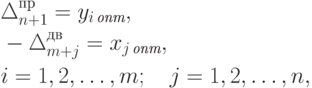$\begin{align*} & \Delta_{n+1}^{\text{пр}} = y_{i \, \textit{опт}} , \\ & -\Delta_{m+j}^{\text{дв}} = x_{j \, \textit{опт}} , \\ & i= 1, 2, \ldots, m; \quad j= 1, 2, \ldots, n, \end{align*}$

( 2.1.31)

где n - количество переменных прямой задачи; m - количество ее ограничений;

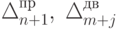$\Delta_{n+1}^{\text{пр}}, \; \Delta_{m+j}^{\text{дв}}$ - соответствующие элементы индексной строки симплекс-таблицы прямой и двойственной задач соответственно.

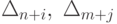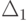При этом, если n+i, где $1 \leq i \leq m$ , больше числа векторов-столбцов матрицы ограничений расширенной формы соответствующей задачи, то элементы $\Delta_{n+i} , \; \Delta_{m+j}$ находятся путем циклической перестановки, начиная с элемента $\Delta_1$ .

Дальше >>

Введение в математическое программирование

Вопросы и ответы

Авторизоваться

Введение в математическое программирование

Вопросы и ответы