Лекция 4: Метод полного исключения. Табличный симплекс – метод. Геометрическая интерпретация задач линейного программирования
2. Табличный симплекс - метод
Основная идея симплекс-метода состоит в переходе от одного допустимого базисного решения к другому таким образом, что значения целевой функции при этом непрерывно возрастают (для задач максимизации).
Предположим, что ограничения задачи сведены к такому виду, что в матрице А имеется единичная подматрица и все свободные члены положительные. Иными словами, пусть матрица ограничений имеет вид
A1x1+...+Anxn+e1xn+e1xn+1+...+emxn+m=A0=[ai0],
где
![e_1 = \left[ \begin{gathered} 1 \\ 0 \\ \ldots \\ 0 \end{gathered} \right] , . ,
e_m = \left[ \begin{gathered} 0 \\ 0 \\ \ldots \\ 1 \end{gathered} \right]
- \text{единичный базис}, \; a_{i0} \geq 0](/sites/default/files/tex_cache/495754404f1c62f8188383073d740393.png)
Применим одну итерацию метода полного исключения к расширенной матрице ограничений Ap=[A1, ..., An, e1, ..., em, A0].
Пусть aij - направляющий элемент преобразования на данной итерации. Тогда в результате преобразований в соответствии с (1.10) получим новые значения свободных членов:
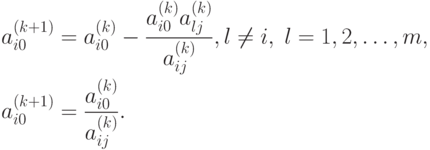 |
( 2.1) |
Исследуем выражения (2.1) и выясним условия, при которых 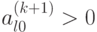 для всех l,
то есть новое базисное решение будет также допустимым.
для всех l,
то есть новое базисное решение будет также допустимым.
По предположению  , тогда
, тогда
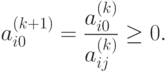
Если 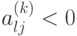 ,
тогда
,
тогда 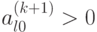 ,
поскольку
,
поскольку 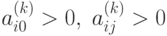 .
.
Если 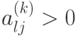 , то
, то
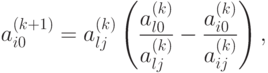
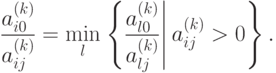 |
( 2.2) |
Преобразование Гаусса называют симплексным преобразованием, когда направляющий элемент определяют по следующим правилам:
a) направляющий столбец j выбирают из условия, что в нем имеется хотя бы один положительный элемент;
б) направляющую строку i выбирают так, чтобы отношение 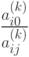 было минимально при условии, что aij>0.
было минимально при условии, что aij>0.
При таком преобразовании в базис вводится вектор Aj и выводится вектор Аi. Теперь надо определить, как выбрать вектор, вводимый в базис, чтобы при этом значение целевой функции увеличилось.
Для этого используют так называемые оценки векторов 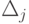 :
:
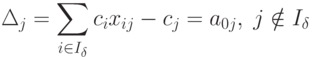 |
( 2.3) |
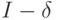 - множество индексов базисных векторов; xij - определяют из условия
- множество индексов базисных векторов; xij - определяют из условия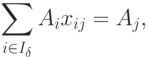 |
( 2.4) |
Величины  равны симплекс-разницам для
переменных {xj} с противоположным знаком.
Следовательно, для того чтобы значение целевой функции увеличилось,
необходимо выбрать направляющий столбец Аj
с наибольшей по модулю отрицательной оценкой, то есть
равны симплекс-разницам для
переменных {xj} с противоположным знаком.
Следовательно, для того чтобы значение целевой функции увеличилось,
необходимо выбрать направляющий столбец Аj
с наибольшей по модулю отрицательной оценкой, то есть

Для решения задачи симплекс-методом на каждой итерации заполняют симплекс-таблицу 2.1.
| c | c1 | c2 | c3 | . | cj | . | cn | ||
| Bx | a00 | A1 | A2 | A3 | . | 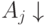 |
. | An | |
| c1 | x1 | a10 | a11 | a12 | a13 | . | a1j | . | a1n |
| c2 | x2 | a20 | a21 | a22 | a23 | . | a2j | . | a2n |
| . | . | . | . | . | . | . | . | . | . |
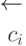 |
xi | ai0 | ai1 | ai2 | ai3 | . | aij | . | ain |
| . | . | . | . | . | . | . | . | . | . |
| cm | xm | am0 | am1 | am2 | am3 | . | amj | . | amn |
 |
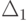 |
 |
 |
. | 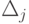 |
. | 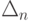 |
Последняя строка таблицы - индексная - служит для определения
направляющего столбца. Ее элементы 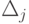 определяют
по формуле (2.3). Очевидно, для всех базисных векторов {Ai} i=1,.,m оценки
определяют
по формуле (2.3). Очевидно, для всех базисных векторов {Ai} i=1,.,m оценки 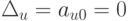 .
.
Значение целевой функции a00 определяется из соотношения
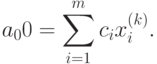
В столбце Bx записываем базисные переменные {xi} i= 1, ..., m. Их значения определяются столбиком свободных членов ai0, то есть
Xi=ai0, i=1,2,.,m.
Направляющие строка Ai и столбец Aj указываются стрелками. Если в качестве направляющего элемента выбран aij, то переход от данной симплекс-таблицы к следующей определяется соотношениями (1.8) - (1.10).
Итак, алгоритм решения задачи ЛП табличным симплекс-методом состоит из этапов.
1. Рассчитывают и заполняют начальную симплекс-таблицу с допустимым единичным базисом, включая индексную строку.
2. В качестве направляющего столбца выбирают Aj, для которого
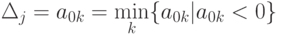
3. Направляющая строка Aі выбирают из условия
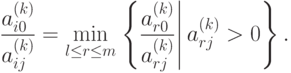
4. Делают один шаг (итерацию) метода полного исключения Гаусса с направляющим элементом aij, для чего используют соотношения (1.8) - (1.10). В частности, элементы индексной строки новой таблицы вычисляют в соответствии с формулой
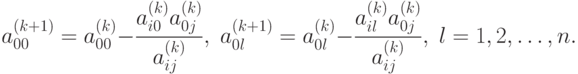
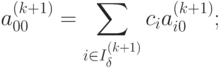 |
( 2.5) |
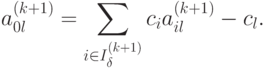 |
( 2.5) |
5. Если все 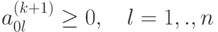 ,
то новое базисное решение
,
то новое базисное решение 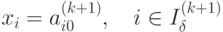 - оптимально. В противном случае переходят к этапу 2 и выполняют
очередную итерацию.
- оптимально. В противном случае переходят к этапу 2 и выполняют
очередную итерацию.
6. Второй, третий и четвертый этапы повторяют до тех пор, пока одна из итераций не закончится одним из двух исходов:
а) все 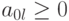 . Это признак (критерий)
оптимальности базисного решения последней симплекс-таблицы ;
. Это признак (критерий)
оптимальности базисного решения последней симплекс-таблицы ;
б) найдется такой 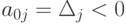 ,
что все элементы этого столбца
,
что все элементы этого столбца 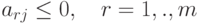 .
Это признак неограниченности целевой функции
.
Это признак неограниченности целевой функции  на множестве допустимых решений задачи.
на множестве допустимых решений задачи.
Назовем некоторые особенности применения табличного симплекс-метода.
Если в качестве начального базиса выбирают базис из свободных
переменных, для которых ci=0, то
оценки для всех небазисных переменных равны 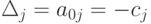 , а соответствующее значение целевой функции
, а соответствующее значение целевой функции
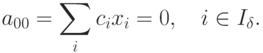
Отсутствие векторов с отрицательными оценками при решении задач максимизации является признаком оптимальности соответствующего базисного решения.
Если существует такой небазисный вектор, для которого оценка отрицательна, а все элементы этого столбца неположительны, то целевая функция задачи в области допустимых решений неограничена.
При решении задач минимизации в базис вводится вектор с наибольшей положительной оценкой, а отсутствие таких векторов является признаком оптимальности последнего базисного решения.
