Лекция 4: Метод полного исключения. Табличный симплекс – метод. Геометрическая интерпретация задач линейного программирования
1. Метод полного исключения
Рассмотренный выше алгоритм симплекс-метода неудобен для программирования и решения задач на ЭВМ. Потребовалась его рационализация как по форме представления информации, так и в способе организации вычислений, чтобы сделать его пригодным для реализации на ЭВМ. С этой целью был разработан табличный вариант симплекс-метода. В его основе лежит метод полного исключения Жордана - Гаусса.
Пусть задана система линейных алгебраических уравнений

В матричной форме данная система имеет следующий вид:
Ax=A0.
Матрица Ap=[A, A0] называется расширенной матрицей. Метод полного исключения Жордана - Гаусса состоит из конечного числа однотипных итераций и заключается в сведении матрицы к единичному виду. Метод основывается на двух операциях:
- одну из строк расширенной матрицы умножают на множитель, отличный от нуля;
- из каждой строки расширенной матрицы вычитают одну строку, умноженную на некоторое число.
Каждое из таких элементарных преобразований (называемых преобразованием Гаусса) приводит к новой системе линейных уравнений, которая эквивалентна начальной системе.
Первая итерация метода полного исключения.
- Среди элементов A выбирают произвольный элемент, отличный от нуля. Его называют направляющим элементом итерации. Строку и столбец, содержащие направляющий элемент, называют направляющими.
- Все элементы направляющей строки расширенной матрицы делят на направляющий элемент. В результате получают направляющую строку с направляющим элементом, равным единице. Далее из элементов каждой строки матрицы A вычитают элементы новой направляющей строки, умноженные на элементы, которые расположены на пересечении данной строки и направляющего столбца.
Матрицу, в которую преобразовалась расширенная
матрица Ap после первой итерации, обозначим  . В ней все элементы
направляющего столбца, кроме направляющего элемента (равного 1),
стали нулями. Совокупность элементов первых n столбцов
матрицы Ap, лежащих вне направляющей строки
и столбца предыдущей (предыдущих) итерации называют главной частью
матрицы
. В ней все элементы
направляющего столбца, кроме направляющего элемента (равного 1),
стали нулями. Совокупность элементов первых n столбцов
матрицы Ap, лежащих вне направляющей строки
и столбца предыдущей (предыдущих) итерации называют главной частью
матрицы  .
.
Вторая и дальнейшие итерации метода проводятся аналогично первой, причем до тех пор, пока имеется возможность выбора направляющего элемента.
Если после k -й итерации главная часть матрицы A_p^{(k)} не содержит ни одного элемента или содержит только нули, то процесс заканчивается.
Пусть процесс оборвался после итерации 1. Предположим вначале, что среди строк матрицы A(l) есть такие, которые не были направляющими ни в одной из предыдущих итераций, например, строка с номером i. Тогда очевидно,
aij=0; j = 1, 2, ., n.
Поскольку для любой строки справедливо
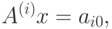 |
( 1.1) |
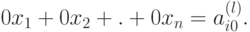 |
( 1.2) |
Если 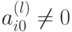 , то уравнение (1.2) противоречиво,
и данная система уравнений неразрешима.
, то уравнение (1.2) противоречиво,
и данная система уравнений неразрешима.
Если 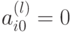 , то уравнение (1.2) представляет
собой тождество и i -я строка может быть отброшена.
, то уравнение (1.2) представляет
собой тождество и i -я строка может быть отброшена.
Перебрав одну за другой все строки матрицы A(l), которые не являлись направляющими, либо устанавливают неразрешимость системы уравнений, либо отбрасывают все нулевые строки.
Таким образом, в системе окажется равно l уравнений. Примем для определенности, что это первые по порядку l уравнений. Тогда полученную систему уравнений можно записать в виде
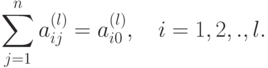 |
( 1.3) |
Пусть i -й направляющей строке соответствует i -й направляющий столбец вследствие соответствующего выбора направляющего элемента. Тогда
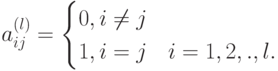 |
( 1.4) |
Следовательно, (1.3) можно записать в виде:
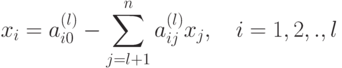 |
( 1.5) |
При xj = 0 (j=l+1, ., n) получим одно из
базисных решений системы уравнений 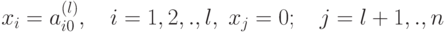 .
.
Задавая для xj произвольные значения 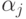 , получим полное множество решений.
, получим полное множество решений.
Если xi - i -я компонента этого решения, то
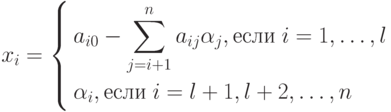 |
( 1.6) |
Обозначим
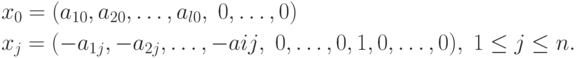
Тогда общее (полное) решение системы линейных уравнений определяется соотношением, аналогичным (1.6):
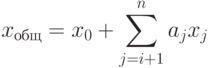 |
( 1.7) |
 - полное решение соответствующей
однородной системы уравнений (то есть при A0=0 ).
- полное решение соответствующей
однородной системы уравнений (то есть при A0=0 ).Обозначим расширенную матрицу системы уравнений после k -й итерации через
![A_p^{(k)} =[a_{i0}^{(k)}, a_{i1}^{(k)},.,a_in^{(k)}], \quad i=1,2,.,m.](/sites/default/files/tex_cache/bedace575d86ade204d6984a43cfe74e.png)
Пусть 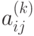 - направляющий элемент
преобразования на (k+1) -й итерации. Тогда в результате (k+1) -й итерации метода полного исключения Гаусса получим
матрицу
- направляющий элемент
преобразования на (k+1) -й итерации. Тогда в результате (k+1) -й итерации метода полного исключения Гаусса получим
матрицу 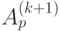 , элементы которой
определяются следующими соотношениями:
, элементы которой
определяются следующими соотношениями:
- для всех элементов направляющей строки
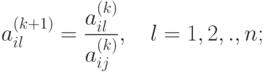
( 1.8) - для элементов направляющего столбца
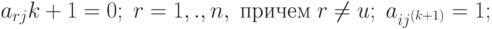
( 1.9) - для всех остальных элементов матрицы
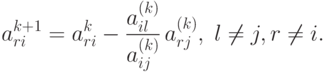
( 1.10)
