Математическое моделирование. Математическая модель в задачах оптимизации. Элементарные математические модели
2. Вариационные принципы. Еще один подход к построению моделей, по своей широте и универсальности сопоставимый с возможностями, даваемыми фундаментальными законами, состоит в применении так называемых вариационных принципов. Они представляют собой весьма общие утверждения о рассматриваемом объекте (системе, явлении) и гласят, что из всех возможных вариантов его поведения (движения, эволюции) выбираются лишь те, которые удовлетворяют определенному условию. Обычно согласно этому условию некоторая связанная с объектом величина достигает экстремального значения при его переходе из одного состояния в другое.
Допустим, автомобиль, движущийся с постоянной скоростью v, должен попасть из точки А в точку В и при этом коснуться некоторой прямой линии С (рис. 1.5).
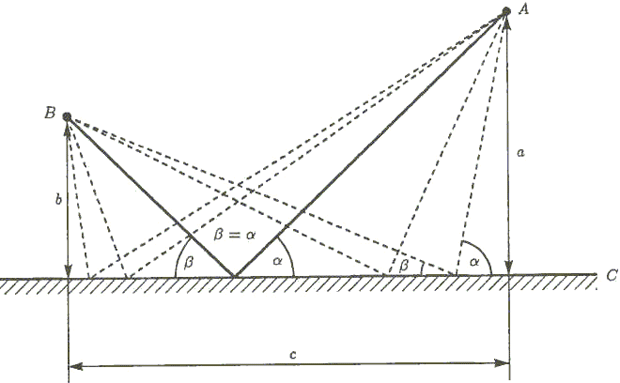
Рис. 1.5. Различные траектории движения из точки А в точку B с касанием прямой С. Жирной линией выделен быстрейший путь
Водитель автомобиля очень торопится и выбирает из множества
траекторий путь, требующий минимальных затрат времени. Представим
затраченное время как функцию величины  - угла
между прямой и отрезком пути от точки А до прямой:
- угла
между прямой и отрезком пути от точки А до прямой:
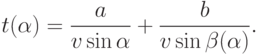
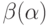 - угол между прямой и отрезком пути
из точки касания до точки В.
- угол между прямой и отрезком пути
из точки касания до точки В.Условие экстремальности 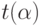 по
аргументу
по
аргументу  означает, что
означает, что

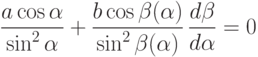 |
( 7) |
Для любых значений  справедливо равенство
справедливо равенство
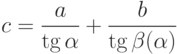
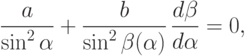 |
( 8) |
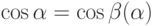
 и
и  .
.Далее нетрудно найти сами значения 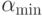 ,
, 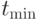 через заданные величины а, b, с.
Однако сейчас для нас важно другое - условие минимальных затрат
времени привело к выбору соответствующей траектории по правилу
"угол падения равен углу отражения". Но ведь такому
закону подчиняется и ход светового луча, попадающего на
отражающую поверхность! Может быть, и в общем случае лучи света
движутся по траекториям, обеспечивающим быстрейшее попадание сигнала
из одной точки в другую? Да, именно так и происходит согласно
известному вариационному принципу Ферма, опираясь на который,
можно получить все основные законы геометрической оптики.
через заданные величины а, b, с.
Однако сейчас для нас важно другое - условие минимальных затрат
времени привело к выбору соответствующей траектории по правилу
"угол падения равен углу отражения". Но ведь такому
закону подчиняется и ход светового луча, попадающего на
отражающую поверхность! Может быть, и в общем случае лучи света
движутся по траекториям, обеспечивающим быстрейшее попадание сигнала
из одной точки в другую? Да, именно так и происходит согласно
известному вариационному принципу Ферма, опираясь на который,
можно получить все основные законы геометрической оптики.
Покажем это, рассмотрев преломление лучей на границе двух сред (рис. 1.6).
Свет, выходящий из точки А, движется в первой
среде со скоростью va, преломляется и,
переходя через линию раздела, двигается во второй среде со
скоростью vb и попадает в точку В. Если  — угол падения луча,
а
— угол падения луча,
а 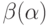 — угол его преломления, то время
прохождения из А в В равно
— угол его преломления, то время
прохождения из А в В равно
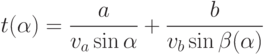
Условие минимальности 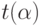 записывается в виде
записывается в виде
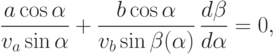
 условие постоянства
величины с по-прежнему выражается формулой (8).
Здесь величины а, b, с имеют тот же смысл, что и в
предыдущем случае. Исключая из последней формулы производную
условие постоянства
величины с по-прежнему выражается формулой (8).
Здесь величины а, b, с имеют тот же смысл, что и в
предыдущем случае. Исключая из последней формулы производную 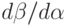 , приходим к равенству
, приходим к равенству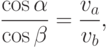 |
( 9) |
Сформулированные применительно к какому-либо классу явлений вариационные принципы позволяют единообразно строить соответствующие математические модели. Их универсальность выражается также в том, что, используя их, можно в определенной степени отвлекаться от конкретной природы процесса. Так, водитель автомобиля, следующий принципу "минимального времени" и желающий попасть из точки А, находящейся на песчаной почве (одна скорость), в точку В, расположенную на травянистом лугу (другая скорость), обязан поехать не по прямой, соединяющей А и B, а по ломанной траектории, сделав необходимое "преломление" на линии, разделяющей песок и траву.

