НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 2: Предмет вычислительной математики. Обусловленность задачи, устойчивость алгоритма, погрешности вычислений. Задача численного дифференцирования

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3791 / 1086 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 53 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

1.8. Задачи для самостоятельного решения

Найти абсолютную предельную погрешность, погрешность по производной и линейную оценку погрешности для функций u = sin t,
$u = \frac{1}{t^2 - 5t + 6}.$

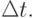
Заданы точка приближения t = t^* и погрешность $\Delta t.$
Определить шаг $\tau$ , при котором погрешность вычисления производной u'(t), приближенно вычисляемой в соответствии с формулами
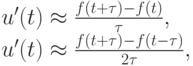
$u^{\prime}(t) \approx \frac{f(t + \tau ) - f(t)}{\tau }, \\ u^{\prime}(t) \approx \frac{f(t + \tau ) - f(t - \tau )}{2\tau } ,$

не превосходит 10³. Известно, что 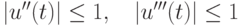$\left|{u^{\prime\prime}(t)}\right| \le 1,\quad \left|{u^{\prime\prime\prime}(t)}\right| \le 1$ для любых t.
Пусть для вычисления функции u = f(t) используется частичная сумма ряда Маклорена
$u(t) \approx u(0) + \frac{u^{\prime}(0)}{1!}t + \ldots + \frac{u^{(n)}(0)}{n!}t^n$
,

причем аргумент задан с погрешностью $\Delta t = 10^{ -3}.$

Найти n такое, чтобы погрешность в определении функции u(y) по данной формуле не превышала 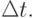$\Delta t.$ Рассмотреть отрезки $t \in [0,1],\quad t \in [10,11] .$

Предложить более совершенный алгоритм для вычисления функций u(t) = sin t, u(t) = e^t на отрезке $t \in [10,11] .$
Определить оптимальный шаг численного дифференцирования $\tau$ при использовании для вычисления производной приближенной формулы
$u^{\prime}(t) \approx \frac{u(t - 2\tau ) - 8(t - \tau ) + 8(t + \tau ) - u(t + 2\tau )}{12t},$

имеющей четвертый порядок точности, если известно, что 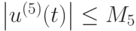$\left|{u^{(5)}(t)}\right| \le M_5$ , а значения функций вычисляются с точностью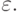 $\varepsilon.$
Вычислить относительную погрешность в определении значения функции u(x,y,z) = x²y²/z⁴, если заданы
$x^{*} = 37,1, y^{*} = 9,87, z^{*} = 6,052, \Delta (x^{*}) = 0,1; \\ \Delta (y^{*}) = 0,05; \Delta (z^{*}) = 0,02.$