НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 2: Предмет вычислительной математики. Обусловленность задачи, устойчивость алгоритма, погрешности вычислений. Задача численного дифференцирования

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3979 / 1247 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 55 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

1.7. Задачи

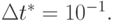
Найти абсолютную предельную погрешность, погрешность по производной, линейную погрешность для функции u = t¹⁰, если заданы точка приближения t^* = 1, значение функции u^* в этой точке и погрешность $\Delta t^{*} = 10^{ -1}.$
Решение : обозначим
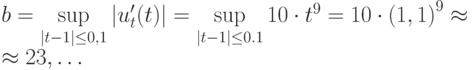
$b=\sup\limits_{\mid{t - 1} \mid \le 0,1} \left|{u^{\prime}_t (t)}\right| = \sup\limits_{\mid{t - 1}\mid \le 0.1} 10 \cdot t^9 = 10 \cdot {(1,1)}^9 \approx \\ \approx 23, \ldots$

Абсолютная предельная погрешность может быть определена как

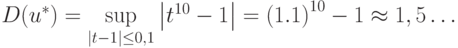
$D(u^*) = \sup\limits_{\mid {t - 1}\mid \le 0,1} \left|{t^{10} - 1}\right| = {(1.1)}^{10} - 1 \approx 1,5 \ldots$
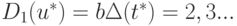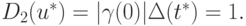
Оценка погрешности u при вычислении значения функции по максимуму производной и линейная оценка соответственно будут $D_{1}(u^{*}) = b\Delta (t^{*}) = 2,3 ...$ ; $D_{2}(u^{*}) = |\gamma (0)|\Delta (t^{*}) = 1.$
Дать линейную оценку погрешности при вычислении неявной функции 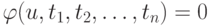$\varphi (u,t_1,t_2, \ldots ,t_n) = 0$ , если известны точка приближения 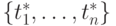$\{ t_1^*, \ldots ,t_n^* \}$ , значение функции в точке приближения u^* и погрешность в определении аргументов $\Delta t_1^*, \ldots ,\Delta t_{n}^* .$
Решение. Дифференцируя по t_j, получим

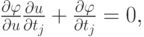
$\frac{\partial \varphi }{\partial u} \frac{\partial u} {\partial t_j} + \frac{\partial \varphi }{\partial t_j} = 0,$

откуда

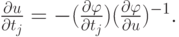
$\frac{\partial u}{\partial t_j} = - (\frac{\partial \varphi }{\partial t_j})(\frac{\partial \varphi }{\partial u})^{ - 1}.$

При заданных 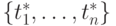$\{ t_1^*, \ldots ,t_n^* \}$ , можно найти u^* как корень уравнения 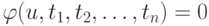$\varphi (u,t_1 ,t_2 , \ldots ,t_{n} ) = 0$ , а затем — значения

$b_j(0) = \left. { - (\frac{\partial \varphi }{\partial t_j })(\frac{\partial \varphi }{\partial u})^{ - 1} } \right|_{(u^*,t_1^* , \ldots ,t_n^* )} ,$

откуда можно получить линейную оценку погрешности функции D₂(u^*).
Вычислить относительную погрешность в определении значения функции
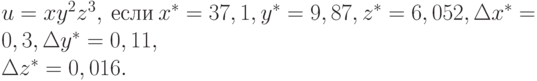
$u = xy^{2}z^{3}, \ если \ x^{*} = 37,1, y^{*} = 9,87, z^{*} = 6,052, \Delta x^{*} = 0,3, \Delta y^{*} = 0,11, \\ \Delta z^{*} = 0,016.$

Решение:

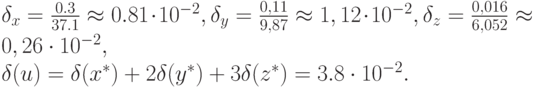
$\delta_x = \frac{0.3}{37.1} \approx 0.81 \cdot 10^{ - 2}, \delta_y = \frac{0,11}{9,87} \approx 1,12 \cdot 10^{ - 2}, \delta_z = \frac{0,016}{6,052} \approx 0,26 \cdot 10^{ - 2}, \\ \delta (u) = \delta (x^*) + 2\delta (y^*) + 3\delta (z^*) = 3.8 \cdot 10^{ - 2} .$
Оценить погрешность в определении корней квадратного уравнения 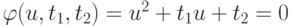$\varphi (u,t_1,t_2) = u^2 + t_1 u + t_2 = 0$ , если заданы приближения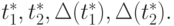 $t_1^*,t_2^*,\Delta (t_1^*),\Delta (t_2^*).$
Пусть u^* — решение уравнения

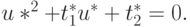
Из формулы

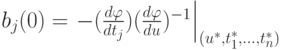
$b_j(0) = \left. { - (\frac{d\varphi }{dt_j})(\frac{d\varphi }{du})^{ - 1}}\right|_{(u^*,t_1^* , \ldots ,t_{n}^*)}$

получим

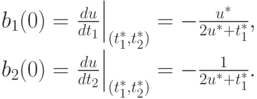
$b_1 (0) = \left. {\frac{du}{dt_1 }} \right|_{(t_1^*,t_2^* )} = - \frac{u^*}{2u^* + t_1^*}, \\ b_2 (0) = \left. {\frac{du}{dt_2 }} \right|_{(t_1^*,t_2^* )} = - \frac{1}{2u^* + t_1^* }.$

Следовательно, линейная оценка будет

$D_2 (u^*) = \frac{\left|{u^*}\right| \cdot \Delta (t_1^*) + \Delta (t_2^* )}{\left|{2u^* + t_1^*}\right|}.$