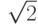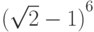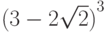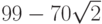Предмет вычислительной математики. Обусловленность задачи, устойчивость алгоритма, погрешности вычислений. Задача численного дифференцирования
1.2. Влияние выбора вычислительного алгоритма на результаты вычислений
Пример 1.6. Пусть необходимо вычислить значение выражения

Избавившись от знаменателя, получаем 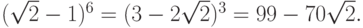
Полагая
а)

в)

и рассматривая эти приближения как разные методы вычисления, получим следующие результаты:
Очевидно, что столь значительное различие в результатах вызвано влиянием
ошибки округления в задании 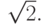
Пример 1.7. Вычисление функции sin x с помощью ряда Тейлора.
Из курса математического анализа известно, что функция синус представляется своим рядом Тейлора
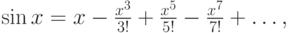
причем радиус сходимости ряда равен бесконечности — ряд сходится при любых значениях x.
Вычислим значения синуса при двух значениях аргумента. Пусть сначала  Будем учитывать лишь члены ряда, большие, чем 10- 4. Выполнив вычисления с четырьмя значащими цифрами, получим sin (0.5236) = 0.5000, что соответствует принятой точности.
Будем учитывать лишь члены ряда, большие, чем 10- 4. Выполнив вычисления с четырьмя значащими цифрами, получим sin (0.5236) = 0.5000, что соответствует принятой точности.
Пусть теперь 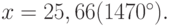 Если вычисления по данной
формуле проводить с восемью значащими цифрами, то получим абсурдный результат:
Если вычисления по данной
формуле проводить с восемью значащими цифрами, то получим абсурдный результат: 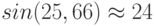 (учитывались члены ряда, большие, чем 10-8 ).
(учитывались члены ряда, большие, чем 10-8 ).
Разумеется, выходом из создавшейся ситуации может быть использование формул приведения.
Пример 1.8. Вычисление функции ex с помощью ряда Тейлора.
Из курса математического анализа известно, что экспонента представляется своим рядом Тейлора

радиус сходимости этого ряда также равен бесконечности.
Приведем некоторые результаты расчетов ( 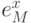 —
значения экспоненты, вычисленные на компьютере).
—
значения экспоненты, вычисленные на компьютере).
Выходом из этой ситуации может быть использование для отрицательных аргументов экспоненты формулы
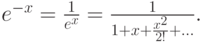
Естественно ожидать рост ошибок округления при вычислении рассматриваемой функции при больших значениях аргумента x. В этом случае можно использовать формулу ex = en + a = enea, где n = [x].
Пример 1.9. Рассмотрим следующий метод вычисления интеграла
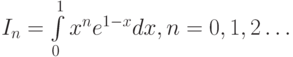
Интегрирование по частям дает
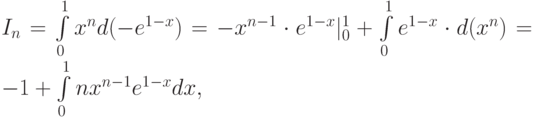
откуда следует
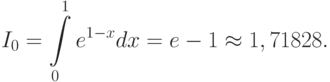
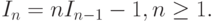
Тогда
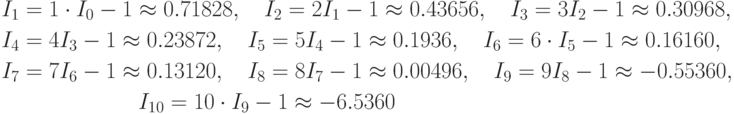
Очевидно, что отрицательные значения при n = 9,10 не имеют смысла. Дело в том, что ошибка, сделанная при округлении I0 до 6-ти значащих цифр сохранилась при вычислении I1, умножилась на 2! при вычислении I2, на 3! — при вычислении I3, и так далее, т.е. ошибка растет очень быстро, пропорционально n!.
Пример 1.10. Рассмотрим методический пример вычислений на модельном компьютере, обеспечивающем точность  Проанализируем причину происхождения ошибки, например, при вычитании двух чисел, взятых с точностью до третьей цифры после десятичной точки u = 1,001, v = 1,002, разность которых составляет
Проанализируем причину происхождения ошибки, например, при вычитании двух чисел, взятых с точностью до третьей цифры после десятичной точки u = 1,001, v = 1,002, разность которых составляет 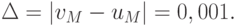
В памяти машины эти же числа представляются в виде
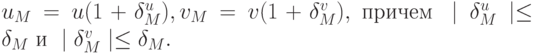
Тогда 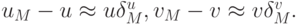
Относительная ошибка при вычислении разности uM - vM будет равна

Очевидно, что 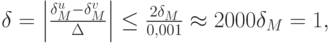 т.е. все значащие цифры могут оказаться неверными.
т.е. все значащие цифры могут оказаться неверными.
Пример 1.11. Рассмотрим рекуррентное соотношение ui+1 = qui, 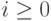 , u0 = a, q > 0, ui > 0.
, u0 = a, q > 0, ui > 0.
Пусть при выполнении реальных вычислений с конечной длиной мантиссы на i -м шаге возникла погрешность округления, и вычисления проводятся с возмущенным значением  , тогда вместо ui+1 получим
, тогда вместо ui+1 получим 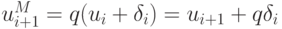 , т.е.
, т.е. 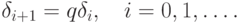
Следовательно, если |q| > 1, то в процессе вычислений
погрешность, связанная с возникшей ошибкой округления, будет возрастать
( алгоритм неустойчив ). В случае  погрешность
не возрастает и численный алгоритм устойчив.
погрешность
не возрастает и численный алгоритм устойчив.
1.3. Экономичность вычислительного метода
Пример 1.12. Пусть требуется вычислить сумму S = 1 + x + x2 + … + x1023 при 0 < x < 1. Для последовательного вычисления 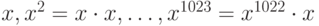 необходимо проделать 1022 умножения, а затем столько же сложений.
необходимо проделать 1022 умножения, а затем столько же сложений.
Однако если заметить, что
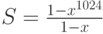

Пример 1.13. Вычисления значений многочленов. Если вычислять значение многочлена P(x) = a0 + a1x + a2x2 + … + anxn "в лоб", т.е. вычислять значения каждого члена и суммировать, то окажется, что необходимо выполнить (n2 + [n/2]) умножений и n сложений. Кроме того, такой способ вычислений может привести к накоплению ошибок округления при вычислениях с плавающей точкой.
Его очевидным улучшением является вычисление каждого члена последовательным умножением на x. Такой алгоритм требует (2n - 1) умножение и n сложений.
Еще более экономичным алгоритмом является хорошо известная в алгебре схема Горнера:
P(x) = ((...((anx + an - 1)x + an - 2)x + ... + a0),
требующая n операций сложения и n операций умножения. Этот метод был известен в средние века в Китае под названием Тянь-Юань и был заново открыт в Европе в начале XIX века англичанином Горнером и итальянцем Руффини.
Пример 1.14. Рассмотрим систему линейных алгебраических уравнений (СЛАУ) вида 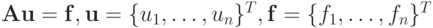 , с трехдиагональной матрицей
, с трехдиагональной матрицей
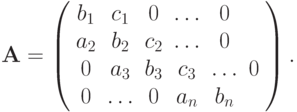
Если проводить решение такой системы без учета специфической структуры матрицы (например, с помощью метода Гаусса), то количество арифметических действий будет порядка n3, если же учесть эту структуру, то количество операций можно уменьшить до n.