|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Маршруты, связность, расстояния
Маршруты и связность в орграфах
Для ориентированного графа можно определить два типа маршрутов. Неориентированный
маршрут (или просто маршрут ) - это чередующаяся
последовательность 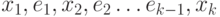 вершин и ребер графа, такая, что для каждого
вершин и ребер графа, такая, что для каждого 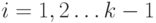 выполняется одно из двух:
выполняется одно из двух: 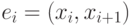 или
или 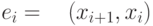 .
Маршрут называется ориентированным
(или ормаршрутом ), если
.
Маршрут называется ориентированным
(или ормаршрутом ), если 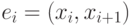 для
каждого
для
каждого  . Таким образом, при движении вдоль маршрута в орграфе
ребра могут проходиться как в направлении ориентации, так и в обратном
направлении, а при движении вдоль ормаршрута - только в направлении
ориентации. Это различие очевидным образом распространяется на пути и
циклы, так что в орграфе можно рассматривать пути и орпути, циклы и
орциклы. Будем говорить, что маршрут соединяет вершины
. Таким образом, при движении вдоль маршрута в орграфе
ребра могут проходиться как в направлении ориентации, так и в обратном
направлении, а при движении вдоль ормаршрута - только в направлении
ориентации. Это различие очевидным образом распространяется на пути и
циклы, так что в орграфе можно рассматривать пути и орпути, циклы и
орциклы. Будем говорить, что маршрут соединяет вершины 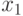 и
и 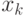 , а ормаршрут ведет
из
, а ормаршрут ведет
из 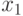 в
в 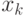 .
.
Соответственно двум типам маршрутов определяются и два типа связности
орграфов. Орграф называется связным (или слабо связным ), если
для каждой пары вершин в нем имеется соединяющий их маршрут; он называется сильно связным, если для
каждой упорядоченной пары вершин
( 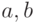 ) в нем имеется ормаршрут, ведущий из
) в нем имеется ормаршрут, ведущий из  в
в  . Максимальные по включению подмножества вершин орграфа, порождающие сильно
связные подграфы, называются его областями сильной связности,
а порождаемые ими подграфы - компонентами сильной связности.
Очевидно, разные области сильной связности
не могут иметь общих вершин, так что
множество вершин каждого орграфа разбивается на области сильной связности.
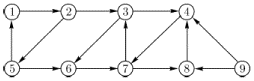
Областями сильной связности орграфа на рис. 2.4 являются множества
. Максимальные по включению подмножества вершин орграфа, порождающие сильно
связные подграфы, называются его областями сильной связности,
а порождаемые ими подграфы - компонентами сильной связности.
Очевидно, разные области сильной связности
не могут иметь общих вершин, так что
множество вершин каждого орграфа разбивается на области сильной связности.
Областями сильной связности орграфа на рис. 2.4 являются множества 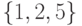 ,
, 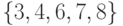 ,
,  .
.
Эйлеровы пути и циклы
Первая теорема теории графов была доказана задолго до того, как стало употребляться словосочетание "теория графов". В 1736 г. появилась работа Эйлера, в которой не только была решена предложенная ему задача о кенигсбергских мостах, но и сформулировано общее правило, позволяющее решить любую задачу такого рода. Интересно, что в одном из писем Эйлер писал по этому поводу:
"... это решение по своему характеру, по-видимому, имеет мало отношения к математике, и мне непонятно, почему следует скорее от математика ожидать этого решения, нежели от какого-нибудь другого человека ..."
На языке теории графов задача состоит в том, чтобы определить, имеется ли
в графе путь, проходящий через все его ребра (напомним, что путь, по
определению, не может дважды проходить по одному ребру). Такой путь
называется эйлеровым
путем, а если он замкнут, то эйлеровым
циклом. В графе, изображенном на рис. 2.5 а,
эйлеров цикл существует -
например, последовательность вершин  ,
,  ,
, 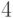 ,
, 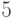 ,
,  ,
,  ,
, 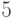 ,
,  ,
,  ,
,  образует
такой цикл. В графе же на рисунке 2.5 б эйлерова цикла нет, но есть
эйлеровы пути, например,
образует
такой цикл. В графе же на рисунке 2.5 б эйлерова цикла нет, но есть
эйлеровы пути, например,  ,
, 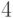 ,
, 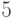 ,
,  ,
,  ,
,  ,
, 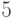 ,
,  ,
,  .
.
Рассмотрим сначала условия существования эйлерова цикла в обыкновенном графе. Ясно, что в несвязном графе эйлеров цикл может существовать только в том случае, когда все его ребра принадлежат одной компоненте связности, а все остальные компоненты - просто изолированные вершины. Поэтому достаточно рассматривать связные графы.
Теорема 5. Эйлеров цикл в связном графе существует тогда и только тогда, когда в нем степени всех вершин четны.
Доказательство.
Необходимость условия очевидна, так как при каждом прохождении цикла через какую-либо вершину используются два ребра - по одному из них маршрут входит в вершину, по другому выходит из нее (это относится и к стартовой вершине - в ней ведь маршрут должен закончиться). Докажем его достаточность.
Пусть  - связный граф, в котором больше одной вершины и
степени
всех вершин четны. Значит, степень каждой вершины не меньше
- связный граф, в котором больше одной вершины и
степени
всех вершин четны. Значит, степень каждой вершины не меньше  ,
поэтому по
теореме 2 в графе
,
поэтому по
теореме 2 в графе  имеется цикл
имеется цикл 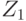 . Если удалить
все ребра
этого цикла из графа
. Если удалить
все ребра
этого цикла из графа  , то получится граф
, то получится граф 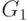 , в
котором
степени вершин также четны. Если в
, в
котором
степени вершин также четны. Если в 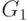 нет ни одного ребра,
то
нет ни одного ребра,
то 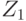 - эйлеров цикл. В противном случае, применяя ту же
теорему 2
к графу, полученному из
- эйлеров цикл. В противном случае, применяя ту же
теорему 2
к графу, полученному из 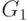 удалением всех изолированных
вершин,
заключаем, что в
удалением всех изолированных
вершин,
заключаем, что в 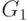 имеется цикл
имеется цикл 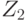 . Удалив
из
. Удалив
из 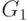 все ребра цикла
все ребра цикла 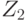 , получим граф
, получим граф 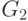 .
Продолжая действовать
таким образом, пока не придем к пустому графу, получим в итоге систему
циклов
.
Продолжая действовать
таким образом, пока не придем к пустому графу, получим в итоге систему
циклов 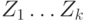 , причем каждое ребро графа принадлежит
в точности одному из них. Покажем теперь, что из этих циклов можно составить
один цикл. Действительно, из того, что исходный граф связен, следует, что
хотя бы один из циклов
, причем каждое ребро графа принадлежит
в точности одному из них. Покажем теперь, что из этих циклов можно составить
один цикл. Действительно, из того, что исходный граф связен, следует, что
хотя бы один из циклов 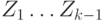 имеет общую вершину
с
имеет общую вершину
с 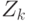 . Допустим, для определенности, что таков цикл
. Допустим, для определенности, что таков цикл  .
Пусть
.
Пусть 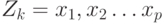 ,
, 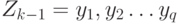 ,
и
,
и  для некоторых
для некоторых  и
и  .
Тогда последовательность вершин
.
Тогда последовательность вершин

очевидно, является циклом, а множество ребер этого цикла есть объединение
множеств ребер циклов  и
и 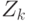 . Таким
образом, получаем систему из меньшего числа циклов, по-прежнему обладающую
тем свойством, что каждое ребро графа принадлежит в точности одному из
них. Действуя далее таким же образом, в конце концов получим один цикл,
который и будет эйлеровым.
. Таким
образом, получаем систему из меньшего числа циклов, по-прежнему обладающую
тем свойством, что каждое ребро графа принадлежит в точности одному из
них. Действуя далее таким же образом, в конце концов получим один цикл,
который и будет эйлеровым.
Теорема 5 верна и для мультиграфов (кстати, в задаче о кенигсбергских мостах ситуация моделируется именно мультиграфом). Она остается верной и при наличии петель, если при подсчете степеней вершин каждую петлю считать дважды.
Теперь нетрудно получить и критерий существования эйлерова пути.
Теорема 6. Эйлеров путь в связном графе существует тогда и только тогда, когда в нем имеется не более двух вершин с нечетными степенями.
Доказательство.
Если в графе нет вершин с нечетными степенями, то, по предыдущей теореме, в нем имеется эйлеров цикл, он является и эйлеровым путем. Не может быть точно одной вершины с нечетной степенью - это следует из теоремы 2 "Начальные понятия теории графов" . Если же имеются точно две вершины с нечетными степенями, то построим новый граф, добавив ребро, соединяющее эти вершины. В новом графе степени всех вершин четны и, следовательно, существует эйлеров цикл (возможно, что при добавлении нового ребра получатся кратные ребра, но, как отмечалось выше, теорема об эйлеровом цикле верна и для мультиграфов). Так как циклический сдвиг цикла - тоже цикл, существует и такой эйлеров цикл, в котором добавленное ребро - последнее. Удалив из этого цикла последнее ребро, получим эйлеров путь в исходном графе.
В ориентированном графе под эйлеровым путем (циклом) понимают ориентированный путь (цикл), проходящий через все ребра графа. Ориентированный вариант критерия существования эйлерова цикла формулируется следующим образом.