|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Формальные языки
Автоматное задание языков
Недетерминированные конечные автоматы
с  -переходами. Недетерминированным конечным
автоматом с
-переходами. Недетерминированным конечным
автоматом с  -переходами над
алфавитом
-переходами над
алфавитом  называется набор
называется набор
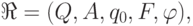
где  — множество состояний,
— множество состояний,  —
алфавит,
—
алфавит,  — начальное
состояние
— начальное
состояние  ,
,  — множество финальных
состояний (
— множество финальных
состояний ( 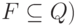 и
и 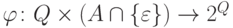 — переходная функция.
— переходная функция.
Такой автомат можно представить нагруженным ориентированным мультиграфом
(диаграммой) следующим образом. Вершинами графа объявить состояния, то
есть элементы множества  , и если
, и если 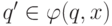 , то из состояния
, то из состояния  в состояние
в состояние 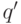 провести дугу,
помеченную символом
провести дугу,
помеченную символом 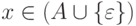 .
.
Язык  , порождаемый автоматом
, порождаемый автоматом  , состоит
из всех слов, которые можно прочитать, двигаясь, начиная со стартового состояния
, состоит
из всех слов, которые можно прочитать, двигаясь, начиная со стартового состояния  , по
ребрам и читая приписанные им символы. Чтение заканчивается в любом из
финальных состояний множества
, по
ребрам и читая приписанные им символы. Чтение заканчивается в любом из
финальных состояний множества  не обязательно при первом
попадании туда. При чтении символов следует воспринимать
не обязательно при первом
попадании туда. При чтении символов следует воспринимать  как пустое слово.
как пустое слово.
Пример.
Пусть алфавит 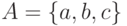 ,
, 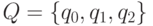 ,
, 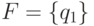 и переходная
функция
и переходная
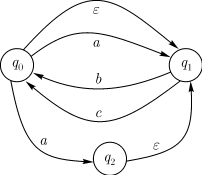
функция  задана таблицей
задана таблицей
Диаграмма автомата изображена на рис. 13.1
Недетерминированные конечные автоматы без  -переходов.
Недетерминированным конечным автоматом без
-переходов.
Недетерминированным конечным автоматом без  -переходов
над алфавитом
-переходов
над алфавитом  называется набор
называется набор
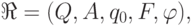
где  — множество состояний,
— множество состояний,  —
алфавит,
—
алфавит,  — начальное
состояние
— начальное
состояние  ,
,  — множество финальных
состояний
— множество финальных
состояний 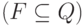 и
и 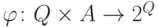 — переходная функция. Такой автомат также можно представить нагруженным ориентированным
мультиграфом (диаграммой). Отличие в том, что дуги теперь могут быть
помечены только символами алфавита
— переходная функция. Такой автомат также можно представить нагруженным ориентированным
мультиграфом (диаграммой). Отличие в том, что дуги теперь могут быть
помечены только символами алфавита  .
.
Язык  , порождаемый таким автоматом
, порождаемый таким автоматом  ,
состоит из всех слов, которые можно прочитать, двигаясь, начиная со стартового состояния
,
состоит из всех слов, которые можно прочитать, двигаясь, начиная со стартового состояния  , по ребрам и читая приписанные им символы. Чтение
заканчивается в любом из финальных состояний множества
, по ребрам и читая приписанные им символы. Чтение
заканчивается в любом из финальных состояний множества  не обязательно при первом
попадании туда.
не обязательно при первом
попадании туда.
Детерминированные конечные автоматы. Детерминированным
конечным автоматом над алфавитом  называется набор
называется набор
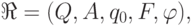
 — множество состояний,
— множество состояний,  —
алфавит,
—
алфавит,  — начальное
состояние
— начальное
состояние  ,
,  — множество финальных
состояний
— множество финальных
состояний 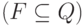 и
и 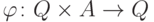 —
переходная функция.
—
переходная функция.Такой автомат также можно представить нагруженным ориентированным
мультиграфом (диаграммой). Отличие от недетерминированного автомата
состоит в том, что из каждого состояния выходит ровно одна дуга,
помеченная конкретной буквой алфавита  .
.
Язык  , порождаемый таким автоматом
, порождаемый таким автоматом  ,
определяется аналогично тому, как это было для недетерминированных автоматов.
,
определяется аналогично тому, как это было для недетерминированных автоматов.
Теорема.
Классы языков, задаваемые детерминированными конечными
автоматами, недетерминированными конечными
автоматами с  -переходами, недетерминированными
конечными автоматами без
-переходами, недетерминированными
конечными автоматами без  -переходов, регулярными
выражениями
совпадают.
-переходов, регулярными
выражениями
совпадают.
Доказательство.
Для доказательства достаточно по регулярному
выражению научиться строить равносильный недетерминированный конечный
автомат с  -переходами (синтез), затем избавляться
от
-переходами (синтез), затем избавляться
от  -переходов, затем
детерминировать и, наконец, по детерминированному автомату строить
регулярное выражение (анализ).
-переходов, затем
детерминировать и, наконец, по детерминированному автомату строить
регулярное выражение (анализ).
Синтез.
Регулярное выражение  представляется автоматом
представляется автоматом
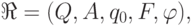
 , алфавит
, алфавит  — произволен,
— произволен,  — начальное состояние,
— начальное состояние, 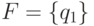 —
множество финальных состояний и переходная функция
—
множество финальных состояний и переходная функция  задается соотношениями
задается соотношениями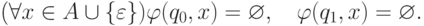
Регулярное выражение 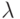 представляется
автоматом
представляется
автоматом 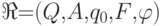 ,
где
,
где  , алфавит
, алфавит  — произволен,
— произволен,  — начальное состояние,
— начальное состояние, 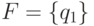 —
множество финальных состояний и переходная функция
—
множество финальных состояний и переходная функция  задается соотношениями
задается соотношениями 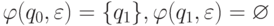 и
и 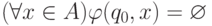 ,
, 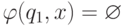 .
.
Регулярное выражение 
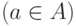 представляется
автоматом
представляется
автоматом 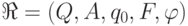 , где
, где  ,
,  —
начальное состояние,
—
начальное состояние, 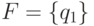 —
множество финальных состояний и переходная функция
—
множество финальных состояний и переходная функция  задается соотношениями
задается соотношениями 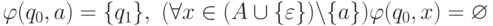 и
и 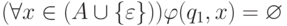 .
.
Для регулярного выражения 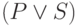 , где
, где  и
и  — регулярные выражения, можно построить задающий
автомат
— регулярные выражения, можно построить задающий
автомат 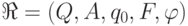 следующим
образом. Пусть автомат
следующим
образом. Пусть автомат 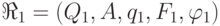 задает
задает 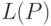 , а автомат
, а автомат 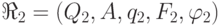 задает
задает  . Не уменьшая общности, можно считать,
что
. Не уменьшая общности, можно считать,
что 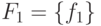 и
и 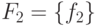 —
одноэлементные и что
—
одноэлементные и что 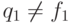 ,
, 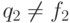 . Положим
. Положим  , где
, где  ,
,  — новые
состояния, и поясним построение автомата
— новые
состояния, и поясним построение автомата  на языке диаграмм.
Состояние
на языке диаграмм.
Состояние  соединим дугами со стартовыми
состояниями
соединим дугами со стартовыми
состояниями 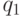 ,
, 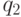 автоматов
автоматов 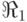 ,
,  и пометим их символом
и пометим их символом  .
Состояния
.
Состояния 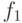 и
и 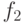 автоматов
автоматов 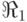 ,
,  соединим дугами с новым
состоянием
соединим дугами с новым
состоянием  и также пометим их символом
и также пометим их символом  .
Начальным состоянием построенного автомата
объявим
.
Начальным состоянием построенного автомата
объявим  , а финальным —
, а финальным —  .
.