Приоритетные очереди

Основные определения

Приоритетная очередь — это абстрактный тип данных, предназначенный для представления взвешенных множеств. Множество называется взвешенным, если каждому его элементу однозначно соответствует число, называемое ключом или весом. Основными операциями над приоритетной очередью являются следующие операции:

• ВСТАВИТЬ в множество новый элемент со своим ключом.
• НАЙТИ в множестве элемент с минимальным ключом. Если элементов с минимальным ключом несколько, то находится один из них. Найденный элемент не удаляется из множества.
• УДАЛИТЬ из множества элемент с минимальным ключом. Если элементов с минимальным ключом несколько, то удаляется один из них.

Дополнительные операции над приоритетными очередями:

• ОБЪЕДИНИТЬ два множества в одно.
• УМЕНЬШИТЬ ключ указанного элемента множества на заданное положительное число.

Приоритетная очередь естественным образом используется в таких задачах, как сортировка элементов массива, поиск во взвешенном неориентированном графе минимального остовного дерева, поиск кратчайших путей от заданной вершины взвешенного графа до его остальных вершин, и во многих других.

Приоритетную очередь можно представить с помощью массива или списка элементов, но такие реализации неэффективны по времени выполнения основных операций. Так, например, поиск элемента с минимальным ключом в неупорядоченном массиве или списке требует последовательного просмотра всех его элементов. Если поддерживать упорядоченность массива или списка по ключу, то "неудобной" окажется операция вставки нового элемента.

Чаще всего приоритетная очередь представляется с помощью корневого дерева или набора корневых деревьев с определенными свойствами. При этом узлам дерева ставятся во взаимно однозначное соответствие элементы рассматриваемого множества.

Соответствие между узлами дерева и элементами множества называется кучеобразным, если для каждого узла соблюдается следующее условие:

Ключ элемента, приписанного узлу , не превосходит ключей, приписанных его потомкам.

Такие представления взвешенных множеств называются кучами. Вид дерева и способ его представления в памяти компьютера подбирается в зависимости от тех операций, которые предполагается выполнять над множеством, и от того, насколько эти операции сказываются на суммарной трудоемкости алгоритма.

Представление приоритетной очереди с помощью d-кучи

Представление приоритетной очереди с помощью -кучи основано на использовании так называемых завершенных -арных деревьев ( ).

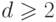Завершенное -арное дерево — это корневое дерево со следующими свойствами:

1. Каждый внутренний узел (то есть узел, не являющийся листом дерева), за исключением, быть может, только одного, имеет ровно потомков. Один узел-исключение может иметь от до 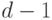потомков.
2. Если — глубина дерева, то для любого такое дерево имеет ровно 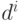узлов глубины .
3. Количество узлов глубины в дереве глубины может варьироваться от до 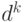. Это свойство является следствием первых двух.

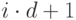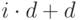Узлы завершенного -арного дерева принято нумеровать следующим образом: корень получает номер 0, потомки узла с номером получают номера: , , , . Такая нумерация удобна тем, что позволяет разместить узлы дерева в массиве в порядке возрастания их номеров, при этом позиции потомков любого узла в массиве легко вычисляются по позиции самого узла. Так же легко по позиции узла вычислить позицию его родителя. Так, для узла, расположенного в позиции , родительский узел располагается в позиции 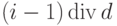, где 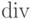— операция деления нацело.

В изображении завершенного -арного дерева узлы одинаковой глубины удобно располагать на одном уровне, при этом потомки одного узла располагаются слева направо в порядке объявленных номеров. При таком рисовании нижний уровень заполняется, возможно, не полностью.

Отметим некоторые простые утверждения о завершенных -арных деревьях, которые будут полезны при анализе трудоемкости основных операций.

Утверждение 1. Длина пути из корня завершенного -арного дерева с 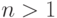узлами в любой лист удовлетворяет неравенствам:

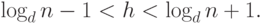
Доказательство Минимальное количество узлов в -куче высоты ( ), по свойствам 2 и 3 -арного дерева, очевидно, равно 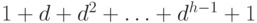(последний уровень содержит лишь один узел).

Максимальное количество узлов в такой -куче равно 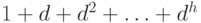(последний уровень содержит 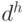узлов). Отсюда имеем неравенства:

Суммируя левую и правую части как геометрические прогрессии, получим

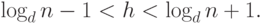
Утверждение 2. Количество узлов высоты не превосходит .

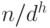Под высотой узла понимается расстояние от него до наиболее далекого потомка. Кучу, содержащую элементов, будем представлять двумя массивами — и , — полагая что — имя элемента, приписанного узлу ; — его ключ. Иногда под удобно понимать сам элемент исходного множества или ссылку на него. В некоторых прикладных задачах нет необходимости помещать в приоритетную очередь ни сами элементы, ни их имена, в таких случаях при организации кучи используется лишь массив .

На рис. 4.1 приведен пример кучи для , 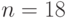. Кружочками изображены узлы дерева, в них записаны элементы массива, представляющие имена элементов кучи.

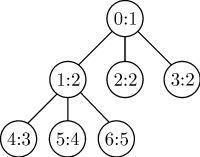
Пример кучи при , 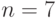для приоритетной очереди, содержащей элементы с ключами 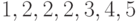, изображен на рис. 4.2, где пара чисел в каждом кружочке обозначает номер узла и ключ соответствующего элемента.

Рис. 4.1.

Рис. 4.2.