|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Формальные языки
Способы задания формальных языков
Прежде всего, для задания формального языка может подойти любое математически корректное определение множества слов в заданном алфавите. Однако если иметь в виду задание, при котором возможно алгоритмическое решение вопроса о принадлежности слова языку, то нужны средства более ограниченные. Наиболее общим из конструктивных способов задания языков является способ, использующий так называемые формальные грамматики.
Формальной грамматикой для порождения формального
языка в алфавите  называется набор
называется набор
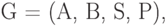
 — алфавит терминальных (основных) символов;
— алфавит терминальных (основных) символов;  — алфавит
нетерминальных (вспомогательных) символов,
— алфавит
нетерминальных (вспомогательных) символов, 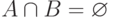 ;
;  — стартовый
символ,
— стартовый
символ,  ;
;  — конечный набор правил
вывода. Каждое правило вывода имеет вид
— конечный набор правил
вывода. Каждое правило вывода имеет вид  , где
, где  ,
,  —
слова в объединенном алфавите
—
слова в объединенном алфавите 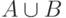 , причем
, причем  содержит хотя бы один символ
из алфавита
содержит хотя бы один символ
из алфавита  .
.Правило  применимо к слову
применимо к слову  ,
если
,
если  является фрагментом слова
является фрагментом слова  . Результатом применения этого правила
к слову
. Результатом применения этого правила
к слову  называется
слово
называется
слово  , полученное заменой любого фрагмента
, полученное заменой любого фрагмента  в слове
в слове  на слово
на слово 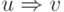 .
.
Если  — результат применения некоторого правила
к слову
— результат применения некоторого правила
к слову  , то
пишем
, то
пишем 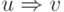 .
.
Если 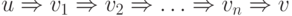 , то
пишем
, то
пишем 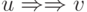 .
.
Язык  , порождаемый грамматикой
, порождаемый грамматикой  , определяется
следующим образом:
, определяется
следующим образом:
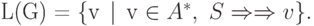
 — множество слов в основном алфавите,
которые могут быть получены из стартового символа
— множество слов в основном алфавите,
которые могут быть получены из стартового символа  путем
конечного числа применений правил грамматики.
путем
конечного числа применений правил грамматики.Классификация Хомского:
- Грамматики типа
 — это грамматики,
не имеющие ограничений на вид правил.
— это грамматики,
не имеющие ограничений на вид правил. - Грамматики типа
 — это грамматики, в которых правила
имеют вид
— это грамматики, в которых правила
имеют вид 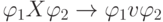 ,
где
,
где  —
нетерминальный символ, а
—
нетерминальный символ, а 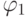 ,
, 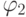 ,
,  — слова в объединенном алфавите. Слова
— слова в объединенном алфавите. Слова 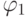 ,
, 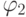 называются
контекстом правила. Эти грамматики (и языки, порождаемые ими) называются
контекстными, так как в описанном правиле символ
называются
контекстом правила. Эти грамматики (и языки, порождаемые ими) называются
контекстными, так как в описанном правиле символ  заменяется
словом
заменяется
словом  , если находится в контексте
, если находится в контексте 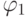 ,
, 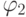 .
. - Грамматики типа
 — это грамматики, в которых правила
имеют вид
— это грамматики, в которых правила
имеют вид 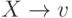 , где
, где  — нетерминальный символ, а
— нетерминальный символ, а  — непустое
слово в объединенном алфавите. Эти грамматики (и языки, порождаемые ими)
называются контекстно-свободными.
— непустое
слово в объединенном алфавите. Эти грамматики (и языки, порождаемые ими)
называются контекстно-свободными. - Грамматики типа
 — это грамматики, в которых правила
имеют вид
— это грамматики, в которых правила
имеют вид 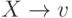 , где
, где  — нетерминальный символ,
а
— нетерминальный символ,
а  может иметь
вид либо
может иметь
вид либо  , либо
, либо 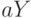 , где
, где  —
символ основного алфавита, а
—
символ основного алфавита, а  — вспомогательного. Языки, порождаемые грамматиками
типа
— вспомогательного. Языки, порождаемые грамматиками
типа  , называются регулярными.
, называются регулярными.
Известно, что класс языков, задаваемых грамматиками типа  ,
является классом рекурсивно перечислимых языков, не совпадающим с классом
рекурсивных языков. На языке теории алгоритмов это означает, что не
существует алгоритма, который по любой грамматике
,
является классом рекурсивно перечислимых языков, не совпадающим с классом
рекурсивных языков. На языке теории алгоритмов это означает, что не
существует алгоритма, который по любой грамматике  типа 0 и
любому слову
типа 0 и
любому слову  отвечает на вопрос "
отвечает на вопрос " 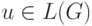 ?". С другой
стороны, существует алгоритм, который, получив на входе грамматику
?". С другой
стороны, существует алгоритм, который, получив на входе грамматику  и слово
и слово  , ответит "да", если
, ответит "да", если 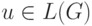 ,
в противном случае он либо ответит "нет", либо будет работать бесконечно.
,
в противном случае он либо ответит "нет", либо будет работать бесконечно.
Классы языков, задаваемых грамматиками типа  ,
,  ,
,  , являются классами рекурсивных языков.
, являются классами рекурсивных языков.
Альтернативный способ задания формальных языков — их описание с помощью различных видов автоматов. Одним из простейших классов языков, имеющих большое прикладное значение, является класс регулярных языков, допускающих описание и с помощью конечных автоматов, и с помощью аналитических выражений.
Регулярные выражения
Регулярные выражения — это аналитический (формульный) способ задания регулярных языков.
Определение.
Регулярным выражением над алфавитом  называется выражение,
построенное по следующим правилам:
называется выражение,
построенное по следующим правилам:
-
 — регулярное выражение;
— регулярное выражение; -
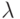 — регулярное выражение;
— регулярное выражение; -
 — регулярное выражение, если
— регулярное выражение, если 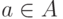 ;
; -
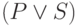 — регулярное выражение, если
— регулярное выражение, если  и
и  — регулярные выражения;
— регулярные выражения; -
 — регулярное выражение,
если
— регулярное выражение,
если  и
и  — регулярные выражения;
— регулярные выражения; -
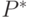 — регулярное выражение, если
— регулярное выражение, если  —
регулярное выражение.
—
регулярное выражение.
Регулярное выражение  задает язык
задает язык 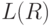 в
соответствии со следующими правилами:
в
соответствии со следующими правилами:
-
 — пустой язык;
— пустой язык; -
 — язык, состоящий из одного пустого слова;
— язык, состоящий из одного пустого слова; -
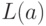 — язык, состоящий из одного
однобуквенного слова
— язык, состоящий из одного
однобуквенного слова  ;
; -
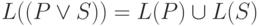 ;
; -
 ;
; -
 .
.
Пример.
Рассмотрим регулярное выражение 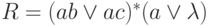 над алфавитом
над алфавитом 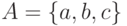 .
Язык
.
Язык 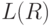 состоит из слов, в которых на нечетных местах стоит
символ
состоит из слов, в которых на нечетных местах стоит
символ  , а на четных
, а на четных  или
или  .
.
Замечание 1.
В регулярных выражениях вместо знака " 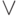 "
часто используют знак "
"
часто используют знак " 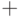 ".
".
Замечание 2. Если дополнить правила построения регулярных выражений еще двумя правилами
-
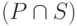 — регулярное выражение,
если
— регулярное выражение,
если  и
и  — регулярные выражения,
— регулярные выражения, -
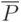 — регулярное выражение, если
— регулярное выражение, если  — регулярное
выражение, и
— регулярное
выражение, и 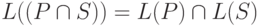 ,
а
,
а 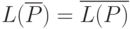 ,
,
то получим так называемые расширенные регулярные выражения. Здесь
дополнение берется до множества всех слов в алфавите  . Если не
использовать дополнение, то получим полурасширенное регулярное выражение.
. Если не
использовать дополнение, то получим полурасширенное регулярное выражение.
Как увидим в дальнейшем, использование расширенных регулярных выражений не расширяет класса регулярных языков.
Замечание 3.
Используя описанную выше интерпретацию
регулярных выражений, мы будем вместо соотношения 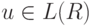 писать
писать  .
.
