|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Формальные языки
Решение уравнений в словах
Рассмотрим уравнение вида 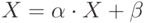 ,
где
,
где  и
и  — формальные языки над
некоторым алфавитом
— формальные языки над
некоторым алфавитом  .
.
Теорема.
Если 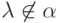 , то уравнение
, то уравнение 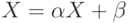 имеет единственное решение
имеет единственное решение 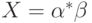 .
Если
.
Если 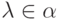 , то
, то 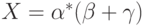 будет решением уравнения
будет решением уравнения 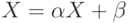 при любом
при любом 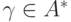 .
.
Доказательство.
Пусть 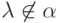 и
и  — решение, тогда,
подставляя его в уравнение, получим
— решение, тогда,
подставляя его в уравнение, получим
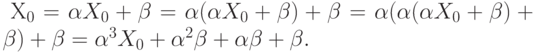
Продолжая выполнять подстановки, видим, что при любом 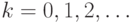 выполняется равенство
выполняется равенство
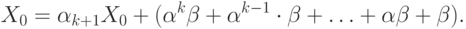 |
( 1) |
Покажем сначала, что 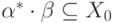 .
Действительно, пусть
.
Действительно, пусть 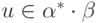 ,
тогда при некотором значении
,
тогда при некотором значении  получим
получим 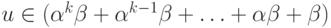 и из (1) при таком значении
и из (1) при таком значении  получаем
получаем 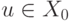 .
.
Осталось показать, что 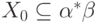 .
Действительно, пусть
.
Действительно, пусть 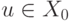 , тогда при любом
, тогда при любом 
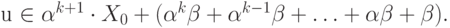
Но так как 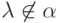 , то при достаточно больших
значениях
, то при достаточно больших
значениях  каждое слово в множестве
каждое слово в множестве 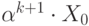 будет длиннее
слова
будет длиннее
слова  и, следовательно,
и, следовательно, 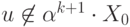 ,
но тогда при таких
,
но тогда при таких 
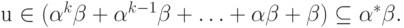
Следовательно, 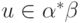 . Итак, мы показали,
что если
. Итак, мы показали,
что если  — решение, то оно задается формулой
— решение, то оно задается формулой  ,
то есть является единственным. Тот факт, что
,
то есть является единственным. Тот факт, что 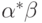 на самом деле — решение, проверяется
простой подстановкой. Второе утверждение теоремы предоставляем доказать читателю.
на самом деле — решение, проверяется
простой подстановкой. Второе утверждение теоремы предоставляем доказать читателю.
Замечание.
Если в уравнении 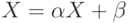 под
под  и
и  понимать регулярные выражения, то в случае
понимать регулярные выражения, то в случае 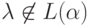 его единственным решением будет регулярное выражение
его единственным решением будет регулярное выражение 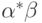 .
.
В случае, когда 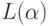 содержит
содержит 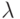 , уравнение
имеет бесконечно много
решений вида
, уравнение
имеет бесконечно много
решений вида 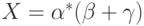 , но здесь под
, но здесь под  можно понимать не только
регулярные выражения, но и выражения в каком-либо формализме, задающие
произвольный язык. Часто в таком случае интересуются наименьшим по
включению решением, так называемой "наименьшей неподвижной точкой".
можно понимать не только
регулярные выражения, но и выражения в каком-либо формализме, задающие
произвольный язык. Часто в таком случае интересуются наименьшим по
включению решением, так называемой "наименьшей неподвижной точкой".
Системы линейных уравнений с регулярными коэффициентми. Под стандартной системой понимают систему вида
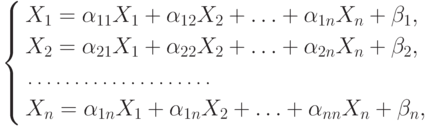
где 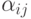 ,
, 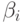 — регулярные выражения,
— регулярные выражения, 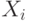 —
переменные (
—
переменные ( 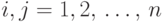 ).
).
Решением системы называется набор 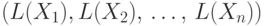 формальных языков, которые при подстановке
вместо соответствующих переменных в уравнения обращают их в равенства.
Удобно на решение смотреть как на отображение
формальных языков, которые при подстановке
вместо соответствующих переменных в уравнения обращают их в равенства.
Удобно на решение смотреть как на отображение  , которое каждой
переменной
, которое каждой
переменной 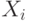 ставит в соответствие язык
ставит в соответствие язык 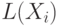 .
Решение
.
Решение 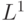 называется наименьшей неподвижной точкой системы,
если для любого другого решения
называется наименьшей неподвижной точкой системы,
если для любого другого решения  выполняются соотношения
выполняются соотношения 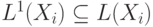 при
при  .
.
Теорема. Каждая стандартная система уравнений имеет единственную неподвижную точку.
Доказательство.
Действительно, нетрудно видеть, что отображение 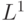 , определяемое по формулам
, определяемое по формулам 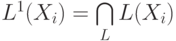 ,
где пересечение берется по всем решениям
,
где пересечение берется по всем решениям  (
( 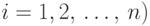 , является искомой неподвижной точкой системы.
, является искомой неподвижной точкой системы.
Решаются такие системы уравнений методом исключения неизвестных. Если,
например,  ,
то первое уравнение можно представить в виде
,
то первое уравнение можно представить в виде 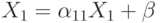 , где
, где 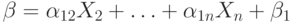 ,
записать его решение описанным выше способом в виде
,
записать его решение описанным выше способом в виде 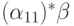 и подставить в остальные уравнения. Получим систему с меньшим числом
неизвестных и так далее.
и подставить в остальные уравнения. Получим систему с меньшим числом
неизвестных и так далее.
