|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Формальные языки
Применение конечных автоматов в программировании
Задача. По заданному регулярному
выражению  над
алфавитом
над
алфавитом  найти в тексте
найти в тексте  наименьший префикс, содержащий слово из
наименьший префикс, содержащий слово из 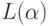 .
.
Решение. Строится регулярное
выражение 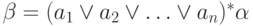 и для него —
недетерминированный конечный автомат
с
и для него —
недетерминированный конечный автомат
с  -переходами. Пусть это будет
автомат
-переходами. Пусть это будет
автомат 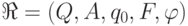 .
Если при чтении текста
.
Если при чтении текста  построенным автоматом мы
приходим в финальное состояние, то это означает, что мы прочитали префикс
текста
построенным автоматом мы
приходим в финальное состояние, то это означает, что мы прочитали префикс
текста  , содержащий слово из языка
, содержащий слово из языка 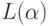 .
.
Алгоритм, моделирующий работу недетерминированного конечного
автомата  с
с  -переходами на входном
слове
-переходами на входном
слове 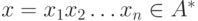 .
.

Оценим трудоемкость приведенного алгоритма. Пусть  , тогда тело цикла
, тогда тело цикла 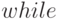 оценивается как
оценивается как  , а тело цикла "
, а тело цикла " 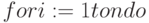 "
как
"
как 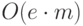 и весь алгоритм имеет трудоемкость
и весь алгоритм имеет трудоемкость 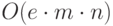 .
.
Анализируя алгоритм построения автомата  с
с  -переходами
по регулярному выражению
-переходами
по регулярному выражению  , легко установить
следующие свойства:
, легко установить
следующие свойства:
-
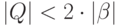 , где
, где  — длина выражения
— длина выражения  с учетом скобок и символов операций;
с учетом скобок и символов операций; -
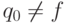 ;
; -
 ;
; -
 .
.
Учитывая приведенные свойства, можем теперь оценить алгоритм, моделирующий
работу автомата  , величиной
, величиной 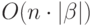 .
.
Рассмотрим теперь задачу, частную по отношению к рассмотренной выше,
полагая, что вместо регулярного выражения  задано одно
слово-образец
задано одно
слово-образец  .
.
Задача. Требуется найти вхождение
заданного слова-образца  в слово-текст
в слово-текст  или установить, что такого вхождения нет.
или установить, что такого вхождения нет.
Определение.
По данному образцу  определим функцию
определим функцию  следующим образом:
следующим образом: 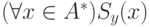 — наибольший
префикс слова
— наибольший
префикс слова  , являющийся суффиксом слова
, являющийся суффиксом слова  .
.
Очевидно, что  .
.
Утверждение 4.
Для любой строки  и любого символа
и любого символа 
 .
.
Действительно, предположим, что  и
и 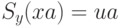 , тогда
, тогда  ,
а
,
а  будет префиксом и суффиксом строки
будет префиксом и суффиксом строки  , причем
, причем  , что противоречит определению
, что противоречит определению 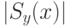 .
.
Утверждение 5.
Пусть 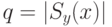 , тогда для любого символа
, тогда для любого символа 
 .
.
Действительно, по предыдущему утверждению, 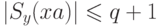 ,
поэтому значение
,
поэтому значение 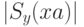 не изменится,
если от строки
не изменится,
если от строки 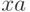 оставить последние
оставить последние 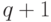 символов,
а именно
символов,
а именно 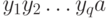 . Построим по слову-образцу
. Построим по слову-образцу  конечный автомат
конечный автомат
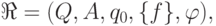
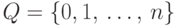 ,
,  ,
,  ,
а переходную функцию
,
а переходную функцию  определим следующим образом:
определим следующим образом: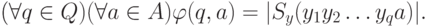
Утверждение 6.
Прочитав текст  , автомат
, автомат 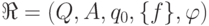 будет находиться в состоянии
будет находиться в состоянии 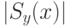 .
.
Алгоритм вычисления функции переходов:

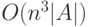 .
.Пример.
Пусть алфавит  и
и 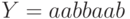 .
Допустим, что, читая текст
.
Допустим, что, читая текст  , мы обнаружили некоторый
префикс
, мы обнаружили некоторый
префикс 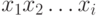 слова
слова  , заканчивающийся
фрагментом
, заканчивающийся
фрагментом 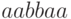 , который является префиксом слова
, который является префиксом слова  , а следующий символ
, а следующий символ 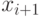 в тексте
в тексте  не
равен
не
равен  , то
есть не совпадает с очередным символом слова
, то
есть не совпадает с очередным символом слова  . Считаем, что
потерпели неудачу, но при этом заметим, что суффикс
. Считаем, что
потерпели неудачу, но при этом заметим, что суффикс 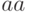 этого
фрагмента является его префиксом и, возможно, он является префиксом
некоторого вхождения слова
этого
фрагмента является его префиксом и, возможно, он является префиксом
некоторого вхождения слова  в
в  .
.
Делая такое предположение, продолжаем читать  , сравнивая
очередные символы слова
, сравнивая
очередные символы слова  с соответствующими, начиная с третьего, символами
слова
с соответствующими, начиная с третьего, символами
слова  в надежде на этот раз обнаружить его вхождение в
в надежде на этот раз обнаружить его вхождение в  .
.
Таким образом, читая  , будем считать, что мы в каждый момент
находимся в некотором состоянии
, будем считать, что мы в каждый момент
находимся в некотором состоянии  , если только что прочитан
префикс
, если только что прочитан
префикс 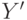 слова
слова  длины
длины  . Если при чтении
следующего символа мы терпим неудачу, то переходим в новое
состояние
. Если при чтении
следующего символа мы терпим неудачу, то переходим в новое
состояние 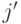 , такое, что
, такое, что 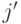 — максимальный
префикс слова
— максимальный
префикс слова 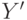 , являющийся его суффиксом.
Функцию, которая состоянию
, являющийся его суффиксом.
Функцию, которая состоянию  ставит
в соответствие
ставит
в соответствие 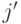 , называют функцией откатов.
В нашем примере ее можно изобразить следующей диаграммой.
, называют функцией откатов.
В нашем примере ее можно изобразить следующей диаграммой.

