| Россия, Новосибирск |
Выразимость в арифметике
Выразимость в арифметике
Рассмотрим сигнатуру, имеющую два двуместных функциональных
символа — сложение и умножение (как обычно, мы будем писать  вместо
вместо 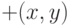 и т. д.) и двуместный предикатный
символ равенства. Рассмотрим интерпретацию этой сигнатуры, носителем
которой является множество
и т. д.) и двуместный предикатный
символ равенства. Рассмотрим интерпретацию этой сигнатуры, носителем
которой является множество 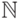 натуральных чисел, а сложение,
умножение и равенство интерпретируются стандартным образом.
натуральных чисел, а сложение,
умножение и равенство интерпретируются стандартным образом.
Выразимые с помощью формул этой сигнатуры предикаты называются арифметическими и играют в математической логике важную роль. Соответствующие множества также называются арифметическими. О них подробно рассказано в другой нашей книжке [5]; оказывается, что почти всякое множество, которое можно описать словами, является арифметическим.
58. Докажите, что существует множество натуральных чисел, не
являющееся арифметическим. (Указание: семейство всех подмножеств
множества 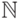 несчетно, а арифметических множеств
счетное число.)
несчетно, а арифметических множеств
счетное число.)
Для начала мы установим арифметичность довольно простых предикатов.
- Предикат
 является арифметическим. В
самом деле, его можно записать как
является арифметическим. В
самом деле, его можно записать как  .
. - Предикаты
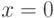 и
и 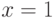 являются арифметическими. В
самом деле,
являются арифметическими. В
самом деле, 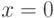 тогда и только тогда, когда
тогда и только тогда, когда  для любого
для любого  (а также когда
(а также когда  ). А
). А 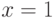 тогда и только
тогда, когда
тогда и только
тогда, когда  представляет собой наименьшее число, отличное
от нуля. (Можно также воспользоваться тем, что
представляет собой наименьшее число, отличное
от нуля. (Можно также воспользоваться тем, что 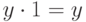 при
любом
при
любом  .)
.) - Вообще для любого фиксированного числа
 предикат
предикат 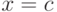 является арифметическим.
(Например, можно написать сумму из большого числа единиц.)
является арифметическим.
(Например, можно написать сумму из большого числа единиц.) - Полезно такое общее наблюдение: если мы уже установили, что какой-то предикат является арифметическим, то в дальнейшей его можно использовать в формулах, как если бы он входил в сигнатуру, поскольку его всегда можно заменить на выражающую его формулу.
- Предикат
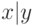 (число
(число  является делителем числа
является делителем числа  ), очевидно, арифметичен (формула
), очевидно, арифметичен (формула 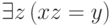 ).
). - Предикат "
 — простое число" арифметичен. В самом деле,
число просто, если оно отлично от
— простое число" арифметичен. В самом деле,
число просто, если оно отлично от  и
любой его делитель равен
и
любой его делитель равен  или самому числу. Это
сразу же записывается в виде формулы.
или самому числу. Это
сразу же записывается в виде формулы. - Операции частного и остатка арифметичны (в том смысле, что
трехместные предикаты "
 есть частное при делении
есть частное при делении  на
на  " и "
" и "  есть остаток при делении
есть остаток при делении  на
на  " арифметичны. Например, первый из них записывается формулой
" арифметичны. Например, первый из них записывается формулой  (как мы уже говорили, использование арифметического предиката
(как мы уже говорили, использование арифметического предиката 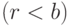 не создает проблем).
не создает проблем). - Этот список можно продолжать: для многих предикатов их определение по существу уже является нужной формулой. Например, свойства "быть наибольшим общим делителем", "быть наименьшим общим кратным", "быть взаимно простыми" все относятся к этой категории.
- Предикат "быть степенью двойки" является арифметическим (хотя это и не столь очевидно, как в предыдущих примерах). В самом деле, это свойство можно переформулировать так: любой делитель либо равен единице, либо четен.
Последнее из наших рассуждений годится для степеней тройки и вообще для степеней любого простого числа. Однако, скажем, для степеней шестерки оно не проходит, и, пожалуй, мы подошли к границе, где без некоторого общего метода не обойтись.
Два наиболее известных способа доказывать арифметичность
основаны на возможности "кодирования" конечных
множеств и последовательностей. Один восходит к Геделю
(так называемая  -функция Геделя),
второй изложен в книге "Теория формальных систем"
[24]. Ее
написал Р.Смаллиан, известный также как автор популярных
сборников "логических задач" и анекдотов. (Один из таких
сборников имеет парадоксальное название "Как же называется
эта книга?" [23].)
-функция Геделя),
второй изложен в книге "Теория формальных систем"
[24]. Ее
написал Р.Смаллиан, известный также как автор популярных
сборников "логических задач" и анекдотов. (Один из таких
сборников имеет парадоксальное название "Как же называется
эта книга?" [23].)
В некоторых отношениях метод Геделя предпочтительней, и мы рассказываем о нем в книжке о вычислимых функциях [5], но сейчас для разнообразия рассмотрим другой способ. Зафиксируем взаимно однозначное соответствие между натуральными числами и двоичными словами:
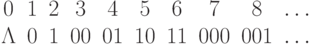
 , надо записать
, надо записать  в двоичной
системе и удалить первую единицу. Например, нулю соответствует
пустое слово
в двоичной
системе и удалить первую единицу. Например, нулю соответствует
пустое слово  , числу
, числу  — слово
— слово 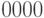 и т. д. Теперь можно говорить об арифметичности предикатов, определенных на
двоичных словах, имея в виду арифметичность соответствующих
предикатов на
и т. д. Теперь можно говорить об арифметичности предикатов, определенных на
двоичных словах, имея в виду арифметичность соответствующих
предикатов на 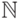 .
.- Предикат "слово
 состоит из одних
нулей" арифметичен. В самом деле, при переходе к числам ему соответствует предикат
"
состоит из одних
нулей" арифметичен. В самом деле, при переходе к числам ему соответствует предикат
" 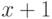 есть степень двойки", который (как мы видели)
арифметичен.
есть степень двойки", который (как мы видели)
арифметичен. - Предикат "слова
 и
и  имеют одинаковую
длину" арифметичен. В самом деле, это означает, что найдется степень
двойки
имеют одинаковую
длину" арифметичен. В самом деле, это означает, что найдется степень
двойки  , для которой
, для которой 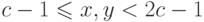 (именно
такой промежуток заполняют числа, которым соответствуют слова одной
длины).
(именно
такой промежуток заполняют числа, которым соответствуют слова одной
длины). - Предикат "слово
 является конкатенацией слов
является конкатенацией слов  и
и  " (проще говоря,
" (проще говоря,  получается приписыванием
получается приписыванием  справа к
слову
справа к
слову  ) арифметичен. В самом деле, его можно выразить так: найдется
слово
) арифметичен. В самом деле, его можно выразить так: найдется
слово 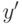 из одних нулей, имеющее ту же длину, что и слово
из одних нулей, имеющее ту же длину, что и слово  , при этом
, при этом 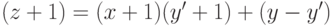 (умножение на
(умножение на  соответствует дописыванию нулей, а добавление
соответствует дописыванию нулей, а добавление 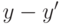 заменяет
нули на буквы слова
заменяет
нули на буквы слова  ).
). - Предикат "слово
 является началом слова
является началом слова  "
арифметичен. В самом деле, это означает, что существует слово
"
арифметичен. В самом деле, это означает, что существует слово  , при котором
, при котором  есть конкатенация
есть конкатенация  и
и  .
. - То же самое верно для предикатов "
 есть конец слова
есть конец слова  ", "
", "  есть подслово слова
есть подслово слова  " (последнее означает,
что найдутся слова
" (последнее означает,
что найдутся слова  и
и  , для которых
, для которых  есть конкатенация
есть конкатенация  ,
,  и
и  ; конкатенация трех слов
выразима через конкатенацию двух).
; конкатенация трех слов
выразима через конкатенацию двух). -
Существует арифметический трехместный предикат
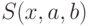 с
такими свойствами: (а) для любых
с
такими свойствами: (а) для любых  и
и  множество
множество 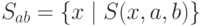 конечно; (б) среди множеств
конечно; (б) среди множеств 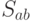 при различных парах
при различных парах 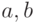 встречаются все
конечные множества. Например, в качестве такого предиката можно взять "
встречаются все
конечные множества. Например, в качестве такого предиката можно взять " 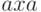 есть подслово слова
есть подслово слова  " (здесь
" (здесь 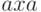 есть конкатенация трех слов:
есть конкатенация трех слов:  ,
,  и снова
и снова  ).
).В самом деле, ясно, что слово
 не длиннее слова
не длиннее слова  , и потому
множество
, и потому
множество 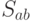 всегда конечно. С другой стороны, пусть
имеется некоторое конечное множество слов
всегда конечно. С другой стороны, пусть
имеется некоторое конечное множество слов  .
Положим
.
Положим 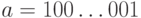 , где число нулей больше длины любого из
слов
, где число нулей больше длины любого из
слов  , и
, и 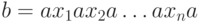 .
.
Последнее утверждение не упоминает явно о словах, и больше они нам не понадобятся: достаточно знать, что конечные множества натуральных чисел можно кодировать парами натуральных чисел в описанном смысле.
Теперь мы можем выразить, что число  является степенью числа
является степенью числа 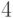 , следующим образом: существует конечное множество
, следующим образом: существует конечное множество  , которое содержит число
, которое содержит число  и обладает таким свойством: всякий
элемент
и обладает таким свойством: всякий
элемент 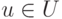 либо равен
либо равен  , либо делится на
, либо делится на 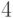 и
и 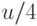 также принадлежит
также принадлежит  . Теперь надо везде заменить множество
. Теперь надо везде заменить множество  на его код
на его код 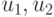 , а утверждение
, а утверждение 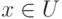 на
на 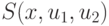 , где
, где  — построенный нами кодирующий предикат.
— построенный нами кодирующий предикат.
Немного сложнее выразить двуместный предикат 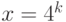 . Здесь
нам хотелось бы сказать так: существует последовательность
. Здесь
нам хотелось бы сказать так: существует последовательность 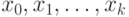 , для которой
, для которой 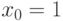 , каждый
следующий член вчетверо больше предыдущего (
, каждый
следующий член вчетверо больше предыдущего ( 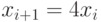 ) и
) и  . Как научиться говорить о последовательностях, если мы умеем
говорить о множествах? Вспомним, что в терминах теории множеств
последовательность есть функция, определенная на начальном
отрезке натурального ряда, то есть конечное множество пар
. Как научиться говорить о последовательностях, если мы умеем
говорить о множествах? Вспомним, что в терминах теории множеств
последовательность есть функция, определенная на начальном
отрезке натурального ряда, то есть конечное множество пар 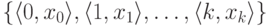 . Пары можно кодировать числами. Например, можно
считать кодом пары
. Пары можно кодировать числами. Например, можно
считать кодом пары  число
число  , поскольку по нему арифметически
восстанавливается
, поскольку по нему арифметически
восстанавливается  (как наибольшее число, квадрат которого
не превосходит
(как наибольшее число, квадрат которого
не превосходит  ), а затем
), а затем  и
и  .
Теперь конечное множество пар можно заменить конечным множеством их кодов,
которое в свою очередь можно закодировать парой чисел.
.
Теперь конечное множество пар можно заменить конечным множеством их кодов,
которое в свою очередь можно закодировать парой чисел.
59. Проведите это рассуждение подробно.
60. Покажите, что двуместный предикат "  есть
есть  -ое
по порядку простое число" арифметичен.
-ое
по порядку простое число" арифметичен.
