| Россия, Новосибирск |
Контрпример
Поиск контрпримера и исчисление секвенций
В этом разделе мы построим другой вариант исчисления высказываний — так называемое исчисление секвенций. Такого рода исчисления изучаются в теории доказательств. Они оказываются более удобными для анализа синтаксической структуры выводов. Их называют исчислениями генценовского типа (по имени Генцена, который начал их изучать). Ранее приведенный вариант исчисления высказываний называют исчислением гильбертовского типа (по имени Гильберта, который использовал подобные исчисления в своей программе формального построения математики).
Для начала мы вообще не будем говорить ничего об аксиомах и
правилах вывода, а рассмотрим задачу поиска контрпримера. Пусть
дана некоторая формула  , про которую мы подозреваем, что она
не является тавтологией, и хотим найти значения переменных, при
которых она ложна. Как это делать? Естественно посмотреть на
структуру формулы
, про которую мы подозреваем, что она
не является тавтологией, и хотим найти значения переменных, при
которых она ложна. Как это делать? Естественно посмотреть на
структуру формулы  . Например, если
. Например, если  имеет
вид
имеет
вид  , то
надо найти значения переменных, при которых формула
, то
надо найти значения переменных, при которых формула  истинна,
а
истинна,
а  ложна. Если
ложна. Если  имеет вид
имеет вид 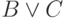 , то
надо найти значения переменных, при которых обе формулы
, то
надо найти значения переменных, при которых обе формулы  и
и  ложны. Если
ложны. Если  имеет вид
имеет вид 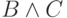 , то надо найти либо
значения переменных, при которых
, то надо найти либо
значения переменных, при которых  ложна, либо значения переменных, при
которых
ложна, либо значения переменных, при
которых  ложна. Тем самым задача поиска контрпримера для
формулы
ложна. Тем самым задача поиска контрпримера для
формулы  сводится к одной или нескольким задачам такого же или
более общего вида (надо обеспечить истинность или ложность одной или
нескольких формул).
сводится к одной или нескольким задачам такого же или
более общего вида (надо обеспечить истинность или ложность одной или
нескольких формул).
Введем необходимую терминологию и обозначения. Будем называть
секвенцией выражение 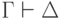 , где
, где  и
и  — некоторые конечные множества формул. (Пока что знак
— некоторые конечные множества формул. (Пока что знак 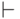 не имеет ничего общего с выводимостью, а только
разделяет два множества формул.) С каждой секвенцией
не имеет ничего общего с выводимостью, а только
разделяет два множества формул.) С каждой секвенцией 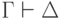 будем связывать задачу поиска таких значений переменных, при
которых все формулы из
будем связывать задачу поиска таких значений переменных, при
которых все формулы из  истинны, а все формулы
из
истинны, а все формулы
из  ложны. Такой набор значений мы по некоторым причинам будем
называть контрпримером к секвенции
ложны. Такой набор значений мы по некоторым причинам будем
называть контрпримером к секвенции 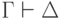 .
Легко проверить, что контрпримеры к секвенции
.
Легко проверить, что контрпримеры к секвенции 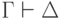 —
это контрпримеры к формуле
—
это контрпримеры к формуле

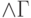 обозначает конъюнкцию формул из
обозначает конъюнкцию формул из  ,
а
,
а 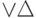 — дизъюнкцию формул из
— дизъюнкцию формул из  ), то есть
те наборы значений, при которых эта формула ложна. При этом конъюнкцию пустого
множества формул мы считаем тождественно истинной, а дизъюнкцию —
тождественно ложной.
), то есть
те наборы значений, при которых эта формула ложна. При этом конъюнкцию пустого
множества формул мы считаем тождественно истинной, а дизъюнкцию —
тождественно ложной.Наша исходная задача поиска контрпримера к формуле  может
быть теперь сформулирована как задача поиска контрпримера к
секвенции
может
быть теперь сформулирована как задача поиска контрпримера к
секвенции 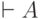 . (Мы позволяем себе писать так для
краткости; полностью следовало бы написать
. (Мы позволяем себе писать так для
краткости; полностью следовало бы написать 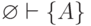 .)
.)
Задачу поиска контрпримера к секвенции можно решать с помощью следующих правил. В каждом из приведенных правил нижний заказ на контрпример выполним, если и только если выполним один из верхних заказов, т. е. нижняя секвенция имеет контрпример тогда и только тогда, когда хотя бы одна из верхних секвенций имеет контрпример.
![\begin{align*}
\frac{\Gamma\vdash A,\Delta\qquad \Gamma\vdash B,\Delta}
{\Gamma\vdash A\wedge B,\Delta}
\qquad&\qquad
\frac{A,B,\Gamma\vdash\Delta}
{A\wedge B,\Gamma\vdash\Delta}
\\[0.7ex]
\frac{\Gamma\vdash A, B,\Delta}
{\Gamma\vdash A\vee B,\Delta}
\qquad&\qquad
\frac{A,\Gamma\vdash \Delta\qquad B,\Gamma\vdash \Delta}
{A\vee B,\Gamma\vdash \Delta}
\\[0.7ex]
\frac{\Gamma,A\vdash B,\Delta}
{\Gamma\vdash A\to B,\Delta}
\qquad&\qquad
\frac{\Gamma\vdash A,\Delta\qquad \Gamma,B\vdash\Delta}
{A\to B,\Gamma\vdash \Delta}
\\[0.7ex]
\frac{A,\Gamma\vdash \Delta}
{\Gamma\vdash \neg A,\Delta}
\qquad&\qquad
\frac{\Gamma\vdash A,\Delta}
{\neg A,\Gamma\vdash \Delta}
\end{align*}](/sites/default/files/tex_cache/51a351b4cdfd29d4fefdda56c67cadc9.png)
Каждое из правил соответствует анализу одной из формул нижней
секвенции. Правила разделены на группы в зависимости от главной
связки анализируемой формулы, и согласованы с таблицами
истинности для этой связки (что легко проверить). Запятая в
правилах используется как сокращение: 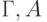 обозначает
обозначает  и т. д.
и т. д.
Как пользоваться этими правилами? Возьмем секвенцию, к которой мы ищем контрпример. Выберем в ней одну из формул слева или справа, посмотрим на главную связку и применим соответствующее правило (написав одну или две секвенции над исходной). Затем к каждой из них снова применим одно из правил и т. д. Постепенно будет расти "дерево поиска контрпримера", причем исходная секвенция будет иметь контрпример тогда и только тогда, когда одна из верхних секвенций (стоящих в "листьях") этого дерева имеет контрпример.
Когда этот процесс обрывается? Это происходит в том случае, если все формулы в оставшихся секвенциях представляют собой переменные, тогда ни одно из наших правил поиска контрпримера не применимо. Но к этому моменту все становится ясным: если в левой и правой части секвенции есть общая переменная, то к ней нет контрпримера (одна и та же переменная не может быть одновременно истинной и ложной). Если же левая и правая часть такой секвенции не пересекаются, то контрпример есть.
Вот как это делается с секвенцией  :
:
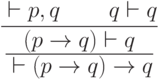
 и
и  ложны (он является
контрпримером к секвенции
ложны (он является
контрпримером к секвенции 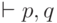 ).
).Напротив, попытка поиска контрпримера к секвенции 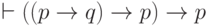 не дает результата:
не дает результата:
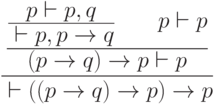
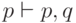 и
и 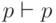 не
имеют контрпримеров. Следовательно, формула
не
имеют контрпримеров. Следовательно, формула 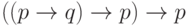 является тавтологией.
является тавтологией.Построенный алгоритм можно одновременно рассматривать как доказательство полноты некоторого "исчисления секвенций".
Аксиомами исчисления секвенций будем называть секвенции, в левых и правых частях которых встречаются только переменные, причем некоторая переменная встречается в обеих частях.
Правилами вывода в исчислении секвенций являются правила нашей таблицы. Каждое из этих правил объявляет выводимой нижнюю секвенцию, если выводимы все верхние. (Процесс вывода естественно представлять в виде дерева, как в наших примерах, но можно развернуть и в последовательность секвенций.)
Теорема 23 (корректность и полнота исчисления секвенций). Секвенция выводима тогда и только тогда, когда она не имеет контрпримера.
Аксиомы не имеют контрпримера. Если все верхние секвенции какого-то правила вывода не имеют контрпримера, то и нижняя секвенция не имеет контрпримера. (Именно так мы подбирали правила: контрпример к нижней секвенции будет контрпримером к одной из верхних.) Следовательно, все выводимые секвенции не имеют контрпримера.
Обратно, пусть секвенция не имеет контрпримера. Тогда описанный процесс поиска контрпримера обрывается на аксиомах и тем самым дает ее вывод.
В частности, если формула  является тавтологией, то секвенция
является тавтологией, то секвенция 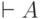 выводима в исчислении секвенций. Это обстоятельство
можно использовать для еще одного доказательства полноты
исчисления высказываний (в стандартной, гильбертовской форме). В
самом деле, для каждой секвенции
выводима в исчислении секвенций. Это обстоятельство
можно использовать для еще одного доказательства полноты
исчисления высказываний (в стандартной, гильбертовской форме). В
самом деле, для каждой секвенции 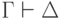 рассмотрим
представляющую ее формулу, то есть формулу
рассмотрим
представляющую ее формулу, то есть формулу  (в левой и правой частях стоят
конъюнкция и дизъюнкция формул из
(в левой и правой частях стоят
конъюнкция и дизъюнкция формул из  и
и  соответственно). Теперь индукцией по построению вывода в
исчислении секвенций надо доказать такой факт: если секвенция
выводима в исчислении секвенций, то представляющая ее формула
выводима в (обычном) исчислении высказываний.
соответственно). Теперь индукцией по построению вывода в
исчислении секвенций надо доказать такой факт: если секвенция
выводима в исчислении секвенций, то представляющая ее формула
выводима в (обычном) исчислении высказываний.
Это требует довольно хлопотной проверки, впрочем. Сначала надо проверить, что конъюнкция и дизъюнкция доказуемо ассоциативны, и потому все равно, как расставлять скобки в формуле, представляющей секвенцию. Затем полезно убедиться, что правила, связанные с отрицанием (два последних правила таблицы) можно применять в обе стороны, не меняя выводимости соответствующей формулы. Другими словами, надо проверить, что формулы
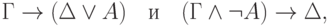
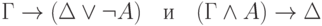
 и
и  можно
считать формулами, а не множествами формул, расставив скобки надлежащим
образом). После этого мы можем переносить формулы из одной части
в другую (меняя их на противоположные), и потому можем считать
одно из множеств
можно
считать формулами, а не множествами формул, расставив скобки надлежащим
образом). После этого мы можем переносить формулы из одной части
в другую (меняя их на противоположные), и потому можем считать
одно из множеств  и
и  пустым, если это нам
удобно. Теперь ссылка на лемму о дедукции и уже известные нам
свойства выводимости завершает рассуждение.
пустым, если это нам
удобно. Теперь ссылка на лемму о дедукции и уже известные нам
свойства выводимости завершает рассуждение.30. Провести это рассуждение подробно.
Естественно возникает вопрос — чем уж так интересно исчисление
секвенций? Какая, собственно говоря, разница — иметь дело с
секвенциями или с формулами, раз всякую секвенцию можно
представить формулой? Принципиальное различие тут в следующем.
Правила вывода в исчислении секвенций таковы, что в их верхнюю
часть входят только подформулы формул, встречающихся в нижней
части. Поэтому в выводе какой-то секвенции не может встретиться
ничего принципиально нового, чего не было в самой секвенции. В
гильбертовском исчислении это далеко не так: мы можем вывести
формулу  из формул
из формул 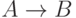 и
и  , при
этом формула
, при
этом формула  может
быть совершенно произвольной. Это же различие объясняет, почему
поиск вывода снизу вверх (как можно теперь называть то, что
раньше называлось поиском контрпримера — мы находим либо
контрпример, либо вывод) для исчисления секвенций происходит
сравнительно однозначно (мы можем по-разному выбирать
расчленяемую формулу, но и только), в то время как искать вывод
в обычном исчислении высказываний, начав с интересующей нас
формулы
может
быть совершенно произвольной. Это же различие объясняет, почему
поиск вывода снизу вверх (как можно теперь называть то, что
раньше называлось поиском контрпримера — мы находим либо
контрпример, либо вывод) для исчисления секвенций происходит
сравнительно однозначно (мы можем по-разному выбирать
расчленяемую формулу, но и только), в то время как искать вывод
в обычном исчислении высказываний, начав с интересующей нас
формулы  и смотря, из чего бы она могла получиться, не
удается (если только не перебирать все формулы подряд).
и смотря, из чего бы она могла получиться, не
удается (если только не перебирать все формулы подряд).
Заметим, что добавление к исчислению секвенций уже упоминавшегося правила сечения

 может быть никак не связана с нижней секвенцией. Отметим, что
добавление правила сечения не нарушает корректности, как легко
проверить, и не может нарушить полноты.
может быть никак не связана с нижней секвенцией. Отметим, что
добавление правила сечения не нарушает корректности, как легко
проверить, и не может нарушить полноты.Задачи о поиске вывода и анализе его структуры, хотя и были одно
время модными в связи с "искусственным интеллектом",
представляют большой интерес, и про них есть целая наука, в
которой исчисления генценовского типа играют центральную роль.
Мы рассмотрели один из вариантов исчисления секвенций для
классического исчисления высказываний; бывают исчисления для
интуиционистских и модальных логик, для исчисления предикатов
и т. д. Исходной мотивацией для рассмотрения такого рода исчислений
было желание доказать непротиворечивость арифметики. Согласно
знаменитой второй теореме Геделя о неполноте без дополнительных аксиом
этого сделать нельзя, но если принять схему аксиом для
трансфинитной индукции по ординалу 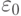 , это удается
сделать, как показал Генцен.
, это удается
сделать, как показал Генцен.
