|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Статистика нечисловых данных
О формулировках законов больших чисел. Пусть 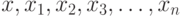 - независимые одинаково распределенные случайные элементы со значениями в
- независимые одинаково распределенные случайные элементы со значениями в 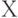 . Закон больших чисел - это утверждение о сходимости эмпирических средних к теоретическому среднему (математическому ожиданию) при росте объема выборки
. Закон больших чисел - это утверждение о сходимости эмпирических средних к теоретическому среднему (математическому ожиданию) при росте объема выборки 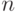 , т.е. утверждение о том, что
, т.е. утверждение о том, что
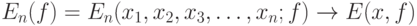 |
( 19) |
при 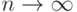 . Однако и слева, и справа в формуле (19) стоят, вообще говоря, множества. Поэтому понятие сходимости в (19) требует обсуждения и определения.
. Однако и слева, и справа в формуле (19) стоят, вообще говоря, множества. Поэтому понятие сходимости в (19) требует обсуждения и определения.
В силу классического закона больших чисел при 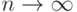
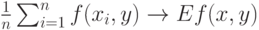 |
( 20) |
в смысле сходимости по вероятности, если правая часть существует (теорема А.Я. Хинчина, 1923 г.).
Если пространство 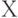 состоит из конечного числа элементов, то из соотношения (20) легко вытекает (см., например, [3, с.192-193]), что
состоит из конечного числа элементов, то из соотношения (20) легко вытекает (см., например, [3, с.192-193]), что
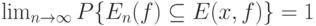 |
( 21) |
Другими словами, 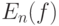 является состоятельной оценкой
является состоятельной оценкой 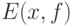 .
.
Если 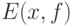 состоит из одного элемента,
состоит из одного элемента, 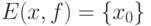 , то соотношение (21) переходит в следующее:
, то соотношение (21) переходит в следующее:
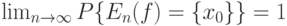 |
( 22) |
Однако с прикладной точки зрения доказательство соотношений (21)-(22) не дает достаточно уверенности в возможности использования 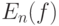 в качестве оценки
в качестве оценки 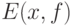 , поскольку в процессе доказательства объем выборки предполагается настолько большим, что при всех
, поскольку в процессе доказательства объем выборки предполагается настолько большим, что при всех 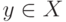 одновременно левые части соотношений (20) сосредотачиваются в непересекающихся окрестностях правых частей.
одновременно левые части соотношений (20) сосредотачиваются в непересекающихся окрестностях правых частей.
Замечание. Если в соотношении (20) рассмотреть сходимость с вероятностью 1, то аналогично (21) получим т.н. усиленный закон больших чисел [3, с.193-194], согласно которому с вероятностью 1 эмпирическое среднее 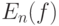 входит в теоретическое среднее
входит в теоретическое среднее 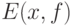 , начиная с некоторого объема выборки
, начиная с некоторого объема выборки 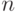 , вообще говоря, случайного,
, вообще говоря, случайного, 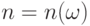 . Мы не будем останавливаться на этом виде сходимости, поскольку в соответствующих постановках, подробно разобранных в монографии [3], нет принципиальных отличий от случая сходимости по вероятности.
. Мы не будем останавливаться на этом виде сходимости, поскольку в соответствующих постановках, подробно разобранных в монографии [3], нет принципиальных отличий от случая сходимости по вероятности.
Если  не является конечным, например,
не является конечным, например, 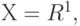 то соотношения (21) и (22) неверны. Поэтому необходимо искать иные формулировки закона больших чисел. В классическом случае сходимости выборочного среднего арифметического к математическому ожиданию, т.е.
то соотношения (21) и (22) неверны. Поэтому необходимо искать иные формулировки закона больших чисел. В классическом случае сходимости выборочного среднего арифметического к математическому ожиданию, т.е. 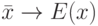 можно записать закон больших чисел так: для любого
можно записать закон больших чисел так: для любого  справедливо предельное соотношение
справедливо предельное соотношение
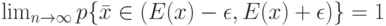 |
( 23) |
В этом соотношении в отличие от (21) речь идет о попадании эмпирического среднего 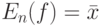 не непосредственно внутрь теоретического среднего
не непосредственно внутрь теоретического среднего 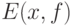 , а в некоторую окрестность теоретического среднего.
, а в некоторую окрестность теоретического среднего.
Обобщим эту формулировку. Как задать окрестность теоретического среднего в пространстве произвольной природы? Естественно взять его окрестность, определенную с помощью какой-либо метрики. Однако полезно обеспечить на ее дополнении до Х отделенность множества значений 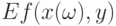 как функции
как функции 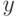 от минимума этой функции на всем
от минимума этой функции на всем 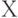 .
.
Поэтому мы сочли целесообразным определить такую окрестность с помощью самой функции 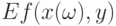 .
.
Определение 3. Для любого 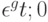 назовем
назовем 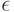 -пяткой функции
-пяткой функции 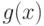 множество
множество
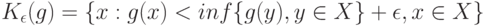
Таким образом, в 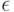 -пятку входят все те
-пятку входят все те  , для которых значение
, для которых значение 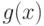 либо минимально, либо отличается от минимального (или от инфимума) не более чем на
либо минимально, либо отличается от минимального (или от инфимума) не более чем на 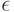 . Так, для
. Так, для  и функции
и функции 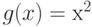 минимум равен 0, а
минимум равен 0, а 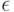 -пятка имеет вид интервала
-пятка имеет вид интервала 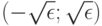 . В формулировке (23) классического закона больших чисел утверждается, что при любом
. В формулировке (23) классического закона больших чисел утверждается, что при любом  вероятность попадания среднего арифметического в
вероятность попадания среднего арифметического в 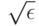 -пятку математического ожидания стремится к 1. Поскольку > 0 произвольно, то вместо
-пятку математического ожидания стремится к 1. Поскольку > 0 произвольно, то вместо 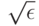 -пятки можно говорить о
-пятки можно говорить о 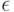 -пятке, т.е. перейти от (23) к эквивалентной записи
-пятке, т.е. перейти от (23) к эквивалентной записи
 |
( 24) |
Соотношение (24) допускает непосредственное обобщение на общий случай пространств произвольной природы.
СХЕМА ЗАКОНА БОЛЬШИХ ЧИСЕЛ. Пусть 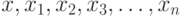 - независимые одинаково распределенные случайные элементы со значениями в пространстве произвольной природы
- независимые одинаково распределенные случайные элементы со значениями в пространстве произвольной природы 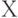 с показателем различия
с показателем различия 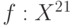 . Пусть выполнены некоторые математические условия регулярности. Тогда для любого
. Пусть выполнены некоторые математические условия регулярности. Тогда для любого  справедливо предельное соотношение
справедливо предельное соотношение
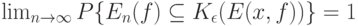 |
( 25) |
Аналогичным образом может быть сформулирована и общая идея усиленного закона больших чисел. Ниже приведены две конкретные формулировки "условий регулярности".
Законы больших чисел. Начнем с рассмотрения естественного обобщения конечного множества - бикомпактного пространства 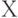 .
.
Теорема 3. В условиях теоремы 1 справедливо соотношение (25).
Доказательство. Воспользуемся построенным при доказательстве теоремы 1 конечным открытым покрытием 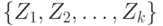 пространства
пространства  таким, что для него выполнено соотношение (3). Построим на его основе разбиение
таким, что для него выполнено соотношение (3). Построим на его основе разбиение 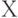 на непересекающиеся множества
на непересекающиеся множества 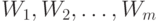 (объединение элементов разбиения
(объединение элементов разбиения 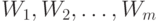 составляет
составляет  ). Это можно сделать итеративно. На первом шаге из
). Это можно сделать итеративно. На первом шаге из  следует вычесть
следует вычесть  - это и будет
- это и будет 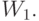 Затем в качестве нового пространства надо рассмотреть разность
Затем в качестве нового пространства надо рассмотреть разность 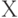 и
и 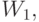 а покрытием его будет
а покрытием его будет 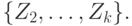 И так до
И так до 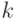 -го шага, когда последнее из рассмотренных покрытий будет состоять из единственного открытого множества
-го шага, когда последнее из рассмотренных покрытий будет состоять из единственного открытого множества 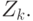 Остается из построенной последовательности
Остается из построенной последовательности 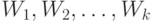 вычеркнуть пустые множества, которые могли быть получены при
осуществлении описанной процедуры (поэтому, вообще говоря,
вычеркнуть пустые множества, которые могли быть получены при
осуществлении описанной процедуры (поэтому, вообще говоря, 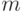 может быть меньше
может быть меньше 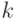 ).
).
В каждом из элементов разбиения 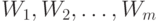 выберем по одной точке, которые назовем центрами разбиения и соответственно обозначим
выберем по одной точке, которые назовем центрами разбиения и соответственно обозначим 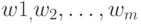 . Это и есть то конечное множество, которым можно аппроксимировать бикомпактное пространство
. Это и есть то конечное множество, которым можно аппроксимировать бикомпактное пространство 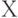 . Пусть
. Пусть 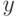 входит в
входит в 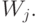 Тогда из соотношения (3) вытекает, что
Тогда из соотношения (3) вытекает, что
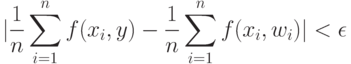 |
( 26) |
Перейдем к доказательству соотношения (25). Возьмем произвольное  . Рассмотрим некоторую точку
. Рассмотрим некоторую точку 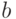 из
из 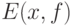 . Доказательство будет основано на том, что с вероятностью, стремящейся к 1, для любого
. Доказательство будет основано на том, что с вероятностью, стремящейся к 1, для любого 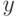 вне
вне  выполнено неравенство
выполнено неравенство
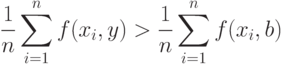 |
( 27) |
Для обоснования этого неравенства рассмотрим все элементы разбиения 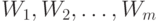 , имеющие непустое пересечение с внешностью
, имеющие непустое пересечение с внешностью 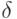 -пятки
-пятки  . Из неравенства (26) следует, что для любого
. Из неравенства (26) следует, что для любого 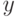 вне
вне  левая часть неравенства (27) не меньше
левая часть неравенства (27) не меньше
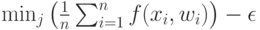 |
( 28) |
где минимум берется по центрам всех элементов разбиения, имеющим непустое пересечение с внешностью 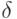 -пятки. Возьмем теперь в каждом таком разбиении точку
-пятки. Возьмем теперь в каждом таком разбиении точку 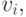 лежащую вне -пятки
лежащую вне -пятки  . Тогда из неравенств (3) и (28) следует, что левая часть неравенства (27) не меньше
. Тогда из неравенств (3) и (28) следует, что левая часть неравенства (27) не меньше
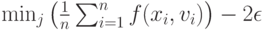 |
( 29) |
В силу закона больших чисел для действительнозначных случайных величин каждая из участвующих в соотношениях (27) и (29) средних арифметических имеет своими пределами соответствующие математические ожидания, причем в соотношении (29) эти пределы не менее
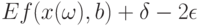
поскольку точки 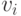 лежат вне
лежат вне 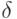 -пятки
-пятки  . Следовательно, при
. Следовательно, при
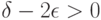
и достаточно большом 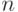 , обеспечивающем необходимую близость рассматриваемого конечного числа средних арифметических к их математическим ожиданиям, справедливо неравенство (27).
, обеспечивающем необходимую близость рассматриваемого конечного числа средних арифметических к их математическим ожиданиям, справедливо неравенство (27).
Из неравенства (27) следует, что пересечение 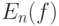 с внешностью
с внешностью  пусто. При этом точка
пусто. При этом точка  может входить в
может входить в 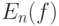 , а может и не входить. Во втором случае
, а может и не входить. Во втором случае 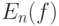 состоит из иных точек, входящих в
состоит из иных точек, входящих в  . Теорема 3 доказана.
. Теорема 3 доказана.
Если Х не является бикомпактным пространством, то необходимо суметь оценить рассматриваемые суммы "на периферии", вне бикомпактного ядра, которое обычно выделяется естественным путем. Один из возможных комплексов условий сформулирован выше в теореме 2.
Теорема 4. В условиях теоремы 2 справедлив закон больших чисел, т.е. соотношение (25).
Доказательство. Будем использовать обозначения, введенные в теореме 2 и при ее доказательстве. Пусть 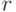 и
и 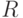 ,
, 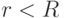 , - положительные числа. Рассмотрим точку
, - положительные числа. Рассмотрим точку  в шаре
в шаре 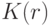 и точку
и точку  вне шара
вне шара 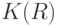 . Поскольку
. Поскольку
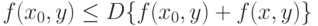
то
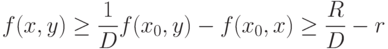 |
( 30) |
Положим

Сравним 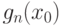 и
и 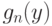 . Выборку
. Выборку 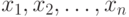 разобьем на две части. В первую часть включим те элементы выборки, которые входят в
разобьем на две части. В первую часть включим те элементы выборки, которые входят в 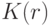 , во вторую - все остальные (т.е. лежащие вне
, во вторую - все остальные (т.е. лежащие вне 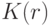 ). Множество индексов элементов первой части обозначим
). Множество индексов элементов первой части обозначим 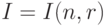 . Тогда в силу неотрицательности
. Тогда в силу неотрицательности 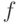 имеем
имеем
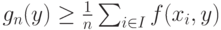
а в силу неравенства (30)

где 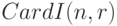 - число элементов в множестве индексов
- число элементов в множестве индексов 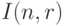 . Следовательно,
. Следовательно,
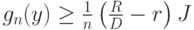 |
( 31) |
где 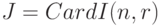 - биномиальная случайная величина
- биномиальная случайная величина 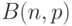 с вероятностью успеха
с вероятностью успеха  . По теореме Хинчина для
. По теореме Хинчина для 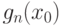 справедлив (классический) закон больших чисел. Пусть
справедлив (классический) закон больших чисел. Пусть  . Выберем
. Выберем 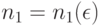 так, чтобы при
так, чтобы при 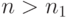 было выполнено соотношение
было выполнено соотношение
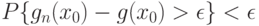 |
( 32) |
где 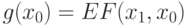 Выберем r так, чтобы вероятность успеха p>0,6. По теореме Бернулли можно выбрать
Выберем r так, чтобы вероятность успеха p>0,6. По теореме Бернулли можно выбрать 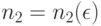 так, чтобы при
так, чтобы при 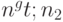
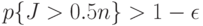 |
( 33) |
Выберем 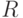 так, чтобы
так, чтобы
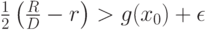
Тогда
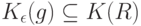 |
( 34) |
и согласно (31), (32) и (33) при 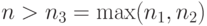 с вероятностью не менее
с вероятностью не менее  имеем
имеем
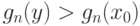 |
( 36) |
для любого 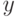 вне
вне 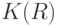 . Из (34) следует, что минимизировать
. Из (34) следует, что минимизировать 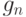 достаточно внутри бикомпактного шара
достаточно внутри бикомпактного шара 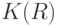 , при этом
, при этом 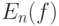 не пусто и
не пусто и
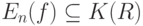 |
( 36) |
с вероятностью не менее 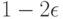 .
.
Пусть 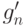 и
и 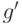 - сужения
- сужения 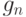 и
и 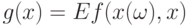 соответственно на
соответственно на 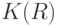 как функций от
как функций от  . В силу (34) справедливо равенство
. В силу (34) справедливо равенство  . Согласно доказанной выше теореме 3 найдется
. Согласно доказанной выше теореме 3 найдется 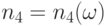 такое, что
такое, что
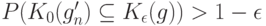
Согласно (36) с вероятностью не менее 
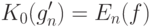
при 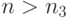 Следовательно, при
Следовательно, при 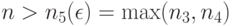 имеем
имеем
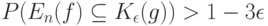
что и завершает доказательство теоремы 4.
Справедливы и иные варианты законов больших чисел, полученные, в частности, в статье [27].
