|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Статистика нечисловых данных
Вероятностные модели конкретных видов объектов нечисловой природы
В настоящем пункте рассмотрены основные вероятностные модели объектов нечисловой природы: дихотомических данных, результатов парных сравнений, бинарных отношений, рангов, объектов общей природы. Обсуждаются различные варианты вероятностных моделей, приведены краткие сведения об их практическом использовании (см. также обзор [14]).
Дихотомические данные. Рассмотрим базовую вероятностную модель дихотомических данных - бернуллиевский вектор (в терминологии энциклопедии [15] - люсиан), т.е. конечную последовательность 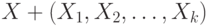 независимых испытаний Бернулли
независимых испытаний Бернулли 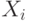 , для которых
, для которых 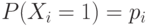 и
и 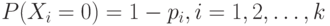 причем вероятности
причем вероятности 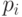 могут быть различны.
могут быть различны.
Бернуллиевские вектора часто применяются при практическом использовании эконометрических методов. Как известно, толерантность на множестве из  элементов можно задать симметричной матрицей
элементов можно задать симметричной матрицей 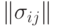 из 0 и 1, на главной диагонали которой стоят 1. Тогда случайная толерантность описывается распределением
из 0 и 1, на главной диагонали которой стоят 1. Тогда случайная толерантность описывается распределением  дихотомических случайных величин
дихотомических случайных величин  а для равномерно распределенной (на множестве всех толерантностей) толерантности эти случайные величины, как можно доказать, оказываются независимыми и принимают значения 0 и 1 с равными вероятностями 1/2. Записав элементы
а для равномерно распределенной (на множестве всех толерантностей) толерантности эти случайные величины, как можно доказать, оказываются независимыми и принимают значения 0 и 1 с равными вероятностями 1/2. Записав элементы 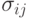 задающей такую толерантность матрицы в строку, получим бернуллиевский вектор с
задающей такую толерантность матрицы в строку, получим бернуллиевский вектор с 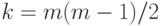 и
и 
В связи с оцениванием по статистическим данным функции принадлежности нечеткой толерантности в 1970-е годы была построена теория случайных толерантностей с такими независимыми 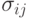 что вероятности
что вероятности 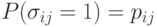 произвольны (см. об этом монографию [3]).
произвольны (см. об этом монографию [3]).
Случайные множества с независимыми элементами использовались как общий язык для описания парных сравнений и случайных толерантностей. В статьях [16] и [17] термин "люсиан" применялся как сокращение для выражения "случайные множества с независимыми элементами". В работе [18], являющейся продолжением [17] и содержащей описание расчетных методов, вытекающих из результатов [17], этот термин не употреблялся вообще, хотя указанный объект (т.е. бернуллиевский вектор) был основным предметом изучения. Это объясняется тем, что изложение в работе [18] шло на языке обработки результатов парных сравнений, которые для прикладника никак не связаны с множествами.
В дальнейшем был выявлен ещё ряд областей, в которых может оказаться полезным разработанный математический аппарат решения различных эконометрических задач, связанных с бернуллиевскими векторами. Перечислим эти области, включая ранее названные: анализ случайных толерантностей; случайные множества с независимыми элементами; обработка результатов независимых парных сравнений; статистические методы анализа точности и стабильности технологического процесса, а также анализ и синтез планов статистического приемочного контроля (по альтернативным, т.е. дихотомическим, признакам); обработка маркетинговых и социологических анкет (с закрытыми вопросами типа "да"-"нет"); обработка социально-психологических и медицинских данных, в частности, ответов на психологические тесты типа MMPI (используемых в задачах управления персоналом), топографических карт (применяемых для анализа и прогноза зон поражения при технологических авариях, распространении коррозии, распространении экологически вредных загряз нений в других ситуациях) и т.д.
Теорию бернуллиевских векторов можно выразить в терминах любой из этих теоретических и прикладных областей. Однако терминология одной из этих областей "режет слух" и приводит к недоразумениям в другой из них. Поэтому мы считаем целесообразным использовать термины "бернуллиевский вектор" в указанном выше значении, не связанном ни с какой из перечисленных областей приложения этой теории (в ряде публикаций в том же значении использовался термин "люсиан").
Распределение бернуллиевского вектора  полностью описывается вектором
полностью описывается вектором  ,т.е. нечетким подмножеством множества
,т.е. нечетким подмножеством множества 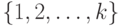 . Действительно, для любого детерминированного вектора
. Действительно, для любого детерминированного вектора 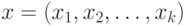 из 0 и 1 имеем
из 0 и 1 имеем
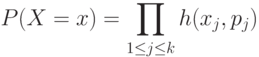
где 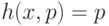 при
при 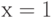 и
и 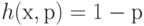 при
при  .
.
Теперь можно уточнить способы использования люсианов при эконометрическом моделировании. Бернуллиевскими векторами можно моделировать: результаты статистического контроля (0-годное изделие, 1-дефектное); результаты маркетинговых и социологических опросов (0-опрашиваемый выбрал первую из двух подсказок, 1-вторую); распределение посторонних включений в материале (0 - нет включения в определенном объеме материала, 1 - есть); результаты испытаний и анализов (0 - нет нарушений требований нормативно-технической документации, 1 - есть такие нарушения); процессы распространения, например, пожаров (0 - нет загорания, 1 - есть; подробнее см. [3, с.215-223]); технологические процессы (0 - процесс находится в границах допуска,1 - вышел из них); ответы экспертов (опрашиваемых) о сходстве объектов (проектов, образцов) и т.д.
Парные сравнения. Общую модель парных сравнений опишем согласно монографии Г. Дэвида [9, с.9]. Предположим, что  объектов
объектов 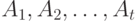 сравниваются попарно каждым из n экспертов. Всего возможных пар для сравнения имеется
сравниваются попарно каждым из n экспертов. Всего возможных пар для сравнения имеется 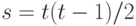 Эксперт с номером
Эксперт с номером  делает
делает 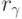 повторных сравнений для каждой из
повторных сравнений для каждой из  возможностей. Пусть
возможностей. Пусть 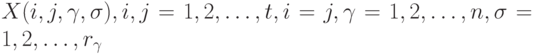 -случайная величина, принимающая значение 1 или 0 в зависимости от того, предпочитает ли эксперт
-случайная величина, принимающая значение 1 или 0 в зависимости от того, предпочитает ли эксперт  объект
объект  или объект
или объект 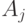 в
в  -м сравнении двух объектов. Предполагается, что все сравнения проводятся независимо друг от друга, так что случайные величины
-м сравнении двух объектов. Предполагается, что все сравнения проводятся независимо друг от друга, так что случайные величины 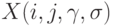 независимы в совокупности, если не считать того, что
независимы в совокупности, если не считать того, что 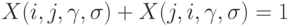 Положим
Положим
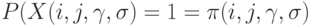
Ясно, что описанная эконометрическая модель парных сравнений представляет собой частный случай бернуллиевского вектора. В этой модели число наблюдений равно числу неизвестных параметров, поэтому для получения статистических выводов необходимо положить априорные условия на 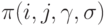 , например [9, c.9]:
, например [9, c.9]:
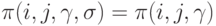 (нет эффекта от повторений);
(нет эффекта от повторений);
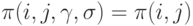 (нет эффекта от повторений и от экспертов).
(нет эффекта от повторений и от экспертов).
Теорию независимых парных сравнений целесообразно разделить на две части - непараметрическую, в которой статистические задачи ставятся непосредственно в терминах 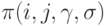 , и параметрическую, в которой вероятности
, и параметрическую, в которой вероятности 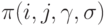 выражаются через меньшее число иных параметров. Ряд результатов непараметрической теории парных сравнений непосредственно вытекает из теории бернуллиевских векторов.
выражаются через меньшее число иных параметров. Ряд результатов непараметрической теории парных сравнений непосредственно вытекает из теории бернуллиевских векторов.
В параметрической теории парных сравнений наиболее популярна так называемая линейная модель [9, c.11], в которой предполагается , что каждому объекту Ai можно сопоставить некоторую "ценность" 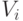 так, что вероятность предпочтения
так, что вероятность предпочтения  (т.е. предполагается дополнительно, что эффект от повторений и от экспертов отсутствует ) выражается следующим образом:
(т.е. предполагается дополнительно, что эффект от повторений и от экспертов отсутствует ) выражается следующим образом:
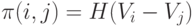 |
( 1) |
где 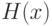 - функция распределения, симметричная относительно 0, т.е.
- функция распределения, симметричная относительно 0, т.е.
 |
( 2) |
при всех  .
.
Широко применяются модели Терстоуна - Мостеллера и Брэдли - Терри , в которых 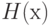 - соответственно функции нормального и логистического распределений. Поскольку функция
- соответственно функции нормального и логистического распределений. Поскольку функция 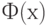 стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1 и функция
стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1 и функция 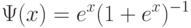 стандартного логистического распределения удовлетворяют (см., например, [19]) соотношению
стандартного логистического распределения удовлетворяют (см., например, [19]) соотношению 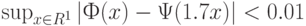 то для обоснованного выбора по статистическим данным между моделями Терстоуна-Мостеллера и Брэдли-Терри необходимо не менее тысячи наблюдений.
то для обоснованного выбора по статистическим данным между моделями Терстоуна-Мостеллера и Брэдли-Терри необходимо не менее тысячи наблюдений.
Соотношение (1) вытекает из следующей модели поведения эксперта: он измерят "ценность" 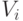 и
и 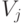 объектов
объектов  и
и 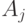 , но с ошибками
, но с ошибками 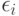 и
и 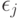 соответственно, а затем сравнивает свои оценки ценности объектов
соответственно, а затем сравнивает свои оценки ценности объектов  и
и  Если
Если  то он предпочитает
то он предпочитает  , в противном случае -
, в противном случае - 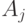 . Тогда
. Тогда
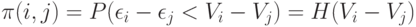 |
( 3) |
Обычно предполагают, что субъективные ошибки эксперта 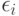 и
и 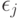 независимы и имеют одно и то же непрерывное распределение. Тогда функция распределения
независимы и имеют одно и то же непрерывное распределение. Тогда функция распределения  из соотношения (3) непрерывна и удовлетворяет функциональному уравнению (2).
из соотношения (3) непрерывна и удовлетворяет функциональному уравнению (2).
Существует много разновидностей моделей парных сравнений, постоянно предполагаются новые. В качестве примера опишем модель парных сравнений, основанную не на процедуре упорядочения, а на определении сходства объектов. Пусть каждому объекту  соответствует точка
соответствует точка  в
в  -мерном евклидовом пространстве
-мерном евклидовом пространстве 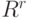 Эксперт "измеряет"
Эксперт "измеряет"  и
и  с ошибками
с ошибками 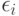 и
и 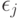 соответственно и в случае, если евклидово расстояние между
соответственно и в случае, если евклидово расстояние между  и
и  меньше 1, заявляет о сходстве объектов
меньше 1, заявляет о сходстве объектов  и
и 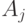 , в противном случае - об их различии. Предполагается, что ошибки
, в противном случае - об их различии. Предполагается, что ошибки 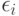 и
и 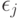 независимы и имеют одно и то же распределение, например, круговое нормальное распределение с нулевым математическим ожиданием и дисперсией координат
независимы и имеют одно и то же распределение, например, круговое нормальное распределение с нулевым математическим ожиданием и дисперсией координат 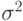 . Целью статистической обработки является опр
еделение по результатам парных сравнений оценок параметров
. Целью статистической обработки является опр
еделение по результатам парных сравнений оценок параметров 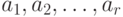 , и
, и 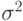 , а также проверка согласия опытных данных с моделью.
, а также проверка согласия опытных данных с моделью.
Рассмотренные модели парных сравнений могут быть обобщены в различных направлениях. Так, можно ввести понятие "ничья "- ситуации, когда эксперт оценивает объекты одинаково. Модели с учетом "ничьих" предполагают, что эксперт может отказаться от выбора одного из объектов и заявить об их эквивалентности, т. е. число возможных ответов увеличивается с 2 до 3. В моделях множественных сравнений эксперту представляется не два объекта, а три или большее число
Модели, учитывающие "ничьи", строятся обычно с помощью используемых в психофизике "порогов чувствительности": если 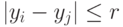 (где
(где  - порог чувствительности), то объекты
- порог чувствительности), то объекты  и
и 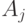 эксперт объявляет неразличимыми. Приведем пример модели с "ничьими", основанной на другом принципе. Пусть каждому объекту
эксперт объявляет неразличимыми. Приведем пример модели с "ничьими", основанной на другом принципе. Пусть каждому объекту  соответствует точка
соответствует точка  в
в  -мерном линейном пространстве. Как и прежде, эксперт "измеряет " объектные точки "
-мерном линейном пространстве. Как и прежде, эксперт "измеряет " объектные точки "  и
и 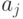 с ошибками
с ошибками 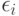 и
и 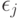 соответственно, т.е. принимает решение на основе
соответственно, т.е. принимает решение на основе  и
и 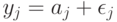 . Если все координаты
. Если все координаты  больше соответствующих координат
больше соответствующих координат 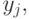 то
то  предпочитается
предпочитается 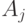 . Соответственно, если каждая координата
. Соответственно, если каждая координата  меньше координаты
меньше координаты  с тем же
номером, то эксперт считает наилучшим объект
с тем же
номером, то эксперт считает наилучшим объект 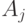 . Во всех остальных случаях эксперт объявляет о ничейной ситуации. Эта модель при
. Во всех остальных случаях эксперт объявляет о ничейной ситуации. Эта модель при 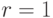 переходит в описанную выше линейную модель. Она связана с принципом Парето в теории группового выбора и предусматривает выбор оптимального по Парето объекта, если он существует (роль согласуемых критериев играют процедуры сравнения значений отдельных координат), и отказ от выбора, если такого объекта нет.
переходит в описанную выше линейную модель. Она связана с принципом Парето в теории группового выбора и предусматривает выбор оптимального по Парето объекта, если он существует (роль согласуемых критериев играют процедуры сравнения значений отдельных координат), и отказ от выбора, если такого объекта нет.
Можно строить модели, учитывающие порядок предъявления объектов при сравнении, зависимость результата сравнения от результатов предшествующих сравнений. Опишем одну из подобных моделей.
Пусть эксперт сравнивает три объекта - 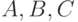 , причем сначала сравниваются
, причем сначала сравниваются  и
и  , потом -
, потом -  и
и  и, наконец,
и, наконец,  и
и  . Для определенности пусть
. Для определенности пусть  будет означать, что
будет означать, что  более предпочтителен, чем
более предпочтителен, чем  . Пусть при предъявлении двух объектов
. Пусть при предъявлении двух объектов

Теперь пусть пара 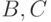 предъявляется после пары
предъявляется после пары  . Естественно предположить, что высокая оценка
. Естественно предположить, что высокая оценка  в первом сравнении повышает вероятность предпочтения
в первом сравнении повышает вероятность предпочтения  и во втором, и, наоборот, отрицательное мнение о
и во втором, и, наоборот, отрицательное мнение о  в первом сравнении сохраняется и при проведении второго сравнения. Это предположение проще всего учесть в модели следующим образом:
в первом сравнении сохраняется и при проведении второго сравнения. Это предположение проще всего учесть в модели следующим образом:
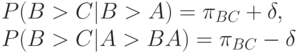
где  - некоторое положительное число, показывающее степень влияния первого сравнения на второе. По аналогичным причинам вероятности исхода третьего сравнения в зависимости от результатов первых двух можно описать так:
- некоторое положительное число, показывающее степень влияния первого сравнения на второе. По аналогичным причинам вероятности исхода третьего сравнения в зависимости от результатов первых двух можно описать так:
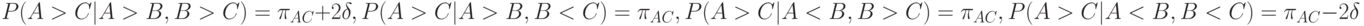
Статистическая задача состоит в определении параметров 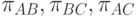 и
и  по результатам сравнений, проведенных
по результатам сравнений, проведенных 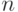 экспертами, и в проверке адекватности модели.
экспертами, и в проверке адекватности модели.
Ясно, что можно рассматривать и другие модели, в частности, учитывающие тягу экспертов к транзитивности ответов. Очевидно, что проблемы построения моделей парных сравнений относятся не к эконометрической теории, а к тем прикладным областям, для решения задач которых развиваются методы парных сравнений, например, к экономике предприятия, стратегическому менеджменту, производственной психологии, изучению поведения потребителей, экспертным оценкам и т. д.
Метод парных сравнений был введен в 1860 г. Г. Т. Фехнером для решения задач психофизики. Расскажем об этом несколько подробнее. Как известно, основателем психофизики по праву считается Густав Теодор Фехнер (1801 - 1887), а год выхода в свет его фундаментальной работы "Элементы психофизики"(1860) - датой рождения новой науки; в этой работе широко применялся предложенный Г.Т. Фехнером метод парных сравнений (обсуждение событий тех лет с современных позиций дано в монографии [9, c.14-16]).
С точки зрения математической статистики приведенные выше модели не представляют большого теоретического интереса: оценки параметров находятся обычно методом максимального правдоподобия, а проверка согласия проводится по критерию отношения правдоподобия или асимптотически эквивалентными ему критериями типа хи-квадрат [9]. Вычислительные процедуры обычно сложны и плохо исследованы; их можно упростить и одновременно повысить обоснованность, перейдя от оценок максимального правдоподобия к одношаговым оценкам [20].
Отметим некоторые сложности при обосновании возможности использовании линейных моделей типа (1) - (3). Эконометрическая теория достаточно проста, когда предполагается, что каждому отдельному сравнению двух объектов соответствуют свои собственные ошибки экспертов, причем все ошибки независимы в совокупности. Однако это предположение отнюдь не очевидно с содержательной точки зрения. В качестве примера рассмотрим три объекта  и
и 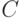 , которые сравнивают попарно:
, которые сравнивают попарно: 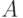 и
и 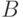 ,
, 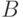 и
и 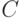 ,
, 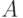 и
и 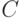 . В соответствии со сказанным, в рассмотрение вводят 6 ошибок одного и того же эксперта:
. В соответствии со сказанным, в рассмотрение вводят 6 ошибок одного и того же эксперта: 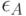 и
и  в первом сравнении,
в первом сравнении, 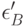 и
и 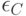 -во втором,
-во втором, 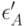 и
и 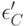 - в третьем, причем все эти 6 случайных величин независимы в совокупности. Между тем естественно думать, что мнения эксперта об одном и том же объекте связаны между собой, т. е.
- в третьем, причем все эти 6 случайных величин независимы в совокупности. Между тем естественно думать, что мнения эксперта об одном и том же объекте связаны между собой, т. е. 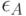 и
и 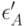 зависимы, равно как
зависимы, равно как  и
и 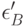 , а также
, а также 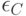 и
и 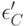 . Более того, если принять, что точка зрения эксперта полностью определена для него самого, то следует положить
. Более того, если принять, что точка зрения эксперта полностью определена для него самого, то следует положить  и соответственно
и соответственно  и
и 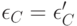 . При этом, напомним, случайные величины
. При этом, напомним, случайные величины  и др. интерпретируется как отклонения мнений отдельных экспертов от истины. Видимо, ошибку эксперта целесообразно считать состоящей из двух слагаемых, а именно: отклонения от истины, вызванного внутренними особенностями эксперта (систематическая погрешность) и колебания мнения эксперта в связи с очередным парным сравнением (случайная погрешность). Игнорирование систематической погрешности облегчает развитие математико-статистической теории, а ее учет приводит к необходимости изучения зависимых парных сравнений.
и др. интерпретируется как отклонения мнений отдельных экспертов от истины. Видимо, ошибку эксперта целесообразно считать состоящей из двух слагаемых, а именно: отклонения от истины, вызванного внутренними особенностями эксперта (систематическая погрешность) и колебания мнения эксперта в связи с очередным парным сравнением (случайная погрешность). Игнорирование систематической погрешности облегчает развитие математико-статистической теории, а ее учет приводит к необходимости изучения зависимых парных сравнений.
При обработке результатов парных сравнений первый этап - проверка согласованности. Понятие согласованности уточняется различными способами, но все они имеют один и тот же смысл проверки однородности обрабатываемого материала, т.е. того, что целесообразно агрегировать мнения отдельных экспертов, объединить данные и совместно их обрабатывать. При отсутствии однородности данные разбиваются на группы (классы, кластеры, таксоны) с целью обеспечения однородности внутри отдельных групп. Естественно, согласованность целесообразно проверять, вводя возможно меньше гипотез о структуре данных. Следовательно, целесообразно пользоваться для этого непараметрической теорией парных сравнений, основанной на теории бернуллиевских векторов.
Хорошо известно, что модели парных сравнений можно с успехом применять в экспертных и экспериментальных процедурах упорядочивания и выбора, в частности, для анализа голосований, турниров, выбора наилучшего объекта (проекта, образца, кандидатуры); в планировании и анализе сравнительных экспериментов и испытаний; в органолептической экспертизе (в частности, дегустации); при изучении поведения потребителей; визуальной колоритмии, определении индивидуальных рейтингов и вообще изучении предпочтений при выборе и т. д. (подробнее см. [3], [9]).
Бинарные отношения. Теорию ранговой корреляции [6], [21] можно рассматривать как теорию статистического анализа случайных ранжировок, равномерно распределенных на множестве всех ранжировок. Так, при обработке данных классического психофизического эксперимента по упорядочению кубиков соответственно их весу, подробно описанного в работе [22], оказалась адекватной следующая т.н. Т-модель ранжирования.
Пусть имеется  объектов
объектов 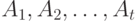 причем каждому объекту
причем каждому объекту  соответствует число
соответствует число 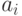 , описывающее его положение на шкале изучаемого признака. Испытуемый упорядочивает объекты так, как если бы оценивал соответствующие им значения с ошибками, т.е. находил
, описывающее его положение на шкале изучаемого признака. Испытуемый упорядочивает объекты так, как если бы оценивал соответствующие им значения с ошибками, т.е. находил 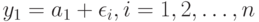 , где
, где 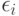 - ошибка при рассмотрении
- ошибка при рассмотрении 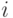 -го объекта, а затем располагал бы объекты в том порядке, в каком располагаются
-го объекта, а затем располагал бы объекты в том порядке, в каком располагаются 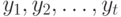 . В этом случае вероятность появления упорядочения
. В этом случае вероятность появления упорядочения  есть
есть 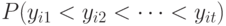 , а ранги
, а ранги 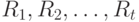 , объектов являются рангами случайных величин
, объектов являются рангами случайных величин 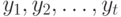 , полученных при их упорядочении в порядке возрастания. Кроме того, для простоты расчетов в модели предполагается, что ошибки испытуемого
, полученных при их упорядочении в порядке возрастания. Кроме того, для простоты расчетов в модели предполагается, что ошибки испытуемого 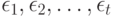 независимы и имеют нормальное распределение с математическим ожиданием 0 и дисперсией
независимы и имеют нормальное распределение с математическим ожиданием 0 и дисперсией 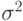 . Как уже отмечалось, бинарное отношение на множестве из
. Как уже отмечалось, бинарное отношение на множестве из 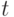 элементов полностью описывается матрицей из 0 и 1 порядка
элементов полностью описывается матрицей из 0 и 1 порядка  . Поэтому задать распределение случайного бинарного отношения - это то же самое, что задать распределение вероятностей на множестве всех матриц описанного вида, состоящем из
. Поэтому задать распределение случайного бинарного отношения - это то же самое, что задать распределение вероятностей на множестве всех матриц описанного вида, состоящем из 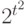 элементов. Пространства ранжировок, разбиений, толерантностей зачастую удобно считать подпространствами пространства всех бинарных отношений, тогда распределения вероятностей на них - частные случаи описанного выше распределения, выделенные тем, что вероятности принадлежности соответствующим подпространствам равны 1. Распределение произвольного бинарного отношения описывается
элементов. Пространства ранжировок, разбиений, толерантностей зачастую удобно считать подпространствами пространства всех бинарных отношений, тогда распределения вероятностей на них - частные случаи описанного выше распределения, выделенные тем, что вероятности принадлежности соответствующим подпространствам равны 1. Распределение произвольного бинарного отношения описывается 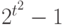 -1 параметрами, распределение случайной ранжировки (без связей) -
-1 параметрами, распределение случайной ранжировки (без связей) -  параметрами, а описанная выше
параметрами, а описанная выше 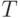 -модель ранжирования
- hЛ
-модель ранжирования
- hЛ 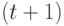 параметром. При
параметром. При 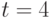 эти числа равны соответственно 65535, 23 и 5. Первое из этих чисел показывает практическую невозможность использования в эконометрических моделях произвольных бинарных отношений, поскольку по имеющимся данным невозможно оценить столь большое число параметров. Приходится ограничиваться теми или иными семействами бинарных отношений - ранжировками, разбиениями, толерантностями и др. Модель произвольной случайной ранжировки при
эти числа равны соответственно 65535, 23 и 5. Первое из этих чисел показывает практическую невозможность использования в эконометрических моделях произвольных бинарных отношений, поскольку по имеющимся данным невозможно оценить столь большое число параметров. Приходится ограничиваться теми или иными семействами бинарных отношений - ранжировками, разбиениями, толерантностями и др. Модель произвольной случайной ранжировки при 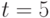 описывается 119 параметрами, при
описывается 119 параметрами, при 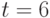 - уже 719 параметрами, при
- уже 719 параметрами, при 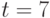 число параметром достигает 5049, что уже явно за возможностями оценивания. В то же время
число параметром достигает 5049, что уже явно за возможностями оценивания. В то же время 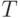 -модель ранжирования при
-модель ранжирования при 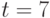 описывается всего 8-ю параметрами, а потому она практически пригодна.
описывается всего 8-ю параметрами, а потому она практически пригодна.
Что естественно предположить относительно распределения случайного элемента со значениями в том или ином пространстве бинарных отношений? Зачастую целесообразно считать, что распределение имеет некий центр, попадание в который наиболее вероятно, а по мере удаления от центра вероятности убывают. Это соответствует естественной модели измерения с ошибкой; в классическом одномерном случае результат подобного измерения описывается унимодальной симметричной плотностью, монотонно возрастающей слева от модального значения, в котором плотность максимальна, и монотонно убывающей справа от него. Чтобы ввести понятие монотонного распределения в пространстве бинарных отношений, будем исходить из метрики в этом пространстве. Воспользовавшись тем, что бинарные отношения 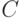 и
и 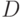 однозначно описываются матрицами
однозначно описываются матрицами 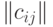 и
и 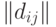 порядка
порядка  соответственно, рассмотрим расстояние (в несколько другой терминологии - метрику) в пространстве бинар
ных отношений
соответственно, рассмотрим расстояние (в несколько другой терминологии - метрику) в пространстве бинар
ных отношений
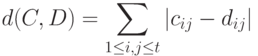 |
( 4) |
Метрика (4) в различных пространствах бинарных отношений - ранжировок, разбиений, толерантностей - может быть введена с помощью соответствующих систем аксиом. В работах [3], [23] дан обзор аксиоматическим подходам к получению метрики (4) в различных пространствах объектов нечисловой природы. В настоящее время метрику (4) обычно называют расстоянием Кемени в честь американского исследователя Джона Кемени, впервые получившего эту метрику исходя из предложенной им системы аксиом для расстояния между упорядочениями (ранжировками). Этой тематике посвящена первая глава учебника [24], на английском языке выпущенном под названием "Математические методы в социальных науках".
В статистике нечисловых данных используются и иные метрики, отличающиеся от расстояния Кемени. Более того, для использования понятия монотонного распределения, о котором сейчас идет речь, нет необходимости требовать выполнения неравенства треугольника, а достаточно, чтобы 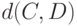 можно было рассматривать как показатель различия. Под показателем различия понимаем такую функцию
можно было рассматривать как показатель различия. Под показателем различия понимаем такую функцию 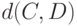 двух бинарных отношений
двух бинарных отношений 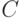 и
и 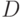 , что
, что 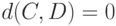 при
при 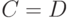 и увеличение
и увеличение 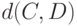 интерпретируется как возрастание различия между
интерпретируется как возрастание различия между 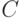 и
и 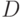 .
.
Определение 1. Распределение бинарного отношения 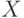 называется монотонным относительно расстояния (показателя различия)
называется монотонным относительно расстояния (показателя различия) 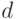 с центром в
с центром в 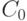 , если из
, если из 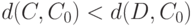 следует, что
следует, что 
Это определение впервые введено в монографии [3, c.196]. Оно может использоваться в любых пространствах бинарных отношений и, более того, в любых пространствах из конечного числа элементов, лишь бы в них была введена функция 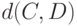 - показатель различия элементов
- показатель различия элементов  и
и 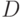 этого пространства. Монотонное распределение унимодально, мода находится в
этого пространства. Монотонное распределение унимодально, мода находится в  .
.
Определение 2. Распределение бинарного отношения  называется симметричным относительно расстояния
называется симметричным относительно расстояния  с центром в
с центром в 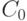 , если существует такая функция
, если существует такая функция ![f:R_+^1 \to [0.1]](/sites/default/files/tex_cache/95c2397c06141a51e103d5ed0482e476.png) что
что
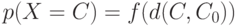 |
( 5) |
Если распределение 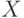 монотонно и таково, что из
монотонно и таково, что из 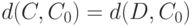 следует
следует  , то оно симметрично. Если функция
, то оно симметрично. Если функция 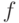 в формуле (5) монотонно строго убывает, то соответствующее распределение монотонно в смысле определения 1.
в формуле (5) монотонно строго убывает, то соответствующее распределение монотонно в смысле определения 1.
Поскольку толерантность на множестве из t элементов задается 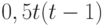 элементами матрицы из 0 и 1 порядка
элементами матрицы из 0 и 1 порядка  , лежащими выше главной диагонали, то распределение на множестве толерантностей задается в общем случае
, лежащими выше главной диагонали, то распределение на множестве толерантностей задается в общем случае 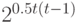 параметрами. Естественно выделить семейство распределений, соответствующее независимым элементам матрицы. Оно задается бернуллиевским вектором (люсианом) с
параметрами. Естественно выделить семейство распределений, соответствующее независимым элементам матрицы. Оно задается бернуллиевским вектором (люсианом) с 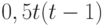 параметрами (выше бернуллиевские вектора рассмотрены подробнее). Математическая техника, необходимая для изучения толерантностей с независимыми элементами, существенно проще, чем в случае ранжировок и разбиений. Здесь легко отказаться от условия равномерности распределения. Этому условию соответствует
параметрами (выше бернуллиевские вектора рассмотрены подробнее). Математическая техника, необходимая для изучения толерантностей с независимыми элементами, существенно проще, чем в случае ранжировок и разбиений. Здесь легко отказаться от условия равномерности распределения. Этому условию соответствует 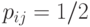 , в то время как статистические методы анализа люсианов, развитые в статистике нечисловых данных (см., например, работы [3],[17], [18]) не налагают никаких существенных ограничений на
, в то время как статистические методы анализа люсианов, развитые в статистике нечисловых данных (см., например, работы [3],[17], [18]) не налагают никаких существенных ограничений на 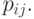
Как уже отмечалось, при обработке мнений экспертов сначала проверяют согласованность. В частности, если мнения экспертов описываются монотонными распределениями, то для согласованности необходимо совпадение центров этих распределений. К сожалению, рассмотренные выше классические методы проверки согласованности для ранжировок, основанные на коэффициентах ранговой корреляции и конкордации, позволяют лишь отвергнуть гипотезу о равнораспределенности, но не установить, можно ли считать, что центры соответствующих экспертам распределений совпадают или же, например, существует две группы экспертов, каждая со своим центром. Теория случайных толерантностей лишена этого недостатка. Отсюда вытекают следующие практические рекомендации.
Пусть цель обработки экспертных данных состоит в получении ранжировки, отражающей групповое мнение. Однако согласно рекомендуемой процедуре экспертного опроса пусть эксперты не упорядочивают объекты, а проводят парные сравнения, сравнивая каждый из рассматриваемых объектов со всеми остальными, причем ровно один раз. Когда ответ эксперта - толерантность, но, вообще говоря, не ранжировка, поскольку в ответах эксперта может нарушаться транзитивность.
Возможны два пути обработки данных. Первый - превратить ответ эксперта в ранжировку (тем или иным способом "спроектировав" на пространство ранжировок), а затем проверять согласованность ранжировок с помощью известных критериев. При этом от толерантности перейти к ранжировке можно, например, так. Будем выбирать ближайшую (в смысле применяемого расстояния) матрицу к матрице ответов эксперта из всех, соответствующих ранжировкам без связей.
Второй путь - проверить согласованность случайных толерантностей, а групповое мнение искать с помощью медианы Кемени (см. ниже) непосредственно по исходным данным, т.е. по толерантностям. Групповое мнение при этом может быть найдено в пространстве ранжировок. Второй путь мы считаем более предпочтительным, поскольку при этом обеспечивается более адекватная проверка согласованности и исключается процедура укладывания мнения эксперта в "прокрустово ложе "ранжировки" (эта процедура может приводить как к потере информации, так и к принципиально неверным выводам).
Области применения статистики бинарных отношений многообразны: ранговая корреляция - оценка величины связи между переменными, измеренными в порядковой шкале; анализ экспертных или экспериментальных упорядочений; анализ разбиений технико-экономических показателей на группы сходных между собой; обработка данных о сходстве (взаимозаменяемости); статистический анализ классификаций; математические вопросы теории менеджмента и др.
