|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Статистика нечисловых данных
Непараметрические оценки плотности в пространствах произвольной природы
Математический аппарат статистики объектов нечисловой природы основан не на свойстве линейности пространства и использовании разнообразных сумм элементов выборок и функций от них, как в классической статистике, а на применении показателей различия, мер близости, метрик, поэтому существенно отличается от классического. В статистике нечисловых данных выделяют общую теорию и статистику в конкретных пространствах нечисловой природы (например, статистику ранжировок). В общей теории есть два основных сюжета. Один связан со средними величинами и асимптотическим поведением решений экстремальных статистических задач, второй - с непараметрическими оценками плотности. Первый сюжет только что рассмотрен, второму посвящена заключительная часть настоящей лекции.
Понятие плотности в пространстве произвольной природы 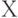 требует специального обсуждения. В пространстве Х должна быть выделена некоторая специальная мера
требует специального обсуждения. В пространстве Х должна быть выделена некоторая специальная мера  , относительно которой будут рассматриваться плотности, соответствующие другим мерам, например, мере
, относительно которой будут рассматриваться плотности, соответствующие другим мерам, например, мере 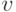 , задающей распределение вероятностей некоторого случайного элемента
, задающей распределение вероятностей некоторого случайного элемента  . В таком случае
. В таком случае 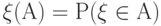 для любого случайного события
для любого случайного события  . Плотность
. Плотность 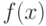 , соответствующая мере
, соответствующая мере 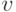 - это такая функция, что
- это такая функция, что 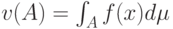 для любого случайного события
для любого случайного события  . Для случайных величин и векторов мера
. Для случайных величин и векторов мера  - это объем множества
- это объем множества  , в математических терминах - мера Лебега. Для дискретных случайных величин и элементов со значениями в конечном множестве
, в математических терминах - мера Лебега. Для дискретных случайных величин и элементов со значениями в конечном множестве 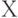 в качестве меры
в качестве меры  естественно использовать считающую меру, которая событию
естественно использовать считающую меру, которая событию  ставит в соответствие число его
элементов. Используют также нормированную случайную меру, когда число точек в множестве
ставит в соответствие число его
элементов. Используют также нормированную случайную меру, когда число точек в множестве  делят на число точек во всем пространстве
делят на число точек во всем пространстве 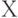 . В случае считающей меры значение плотности в точке
. В случае считающей меры значение плотности в точке  совпадает с вероятностью попасть в точку
совпадает с вероятностью попасть в точку  , т.е.
, т.е. 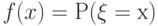 . Таким образом, с рассматриваемой точки зрения стирается грань между понятиями "плотность вероятности" и "вероятность (попасть в точку)".
. Таким образом, с рассматриваемой точки зрения стирается грань между понятиями "плотность вероятности" и "вероятность (попасть в точку)".
Как могут быть использованы непараметрические оценки плотности распределения вероятностей в пространствах нечисловой природы? Например, для решения задач классификации (диагностики, распознавания образов - см.
"Многомерный статистический анализ"
). Зная плотности распределения классов, можно решать основные задачи диагностики - как задачи выделения кластеров, так и задачи отнесения вновь поступающего объекта к одному из диагностических классов. В задачах кластер-анализа можно находить моды плотности и принимать их за центры кластеров или за начальные точки итерационных методов типа 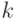 -средних или динамических сгущений. В задачах собственно диагностики (дискриминации, распознавания образов с учителем) можно принимать решения о диагностике объектов на основе отношения плотностей, соответствующих классам. При неизвестных плотностях представляется естественным использовать их состоятельные оценки.
-средних или динамических сгущений. В задачах собственно диагностики (дискриминации, распознавания образов с учителем) можно принимать решения о диагностике объектов на основе отношения плотностей, соответствующих классам. При неизвестных плотностях представляется естественным использовать их состоятельные оценки.
Методы оценивания плотности вероятности в пространствах общего вида предложены и первоначально изучены в работе [31]. В частности, в задачах диагностики объектов нечисловой природы предлагаем использовать непараметрические ядерные оценки плотности типа Парзена - Розенблатта (этот вид оценок и его название впервые были введены в статье [31]). Они имеют вид:
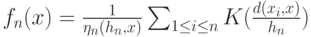
где 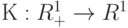 - так называемая ядерная функция,
- так называемая ядерная функция, 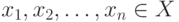 - выборка, по которой оценивается плотность,
- выборка, по которой оценивается плотность, 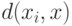 - показатель различия (метрика, расстояние, мера близости) между элементом выборки
- показатель различия (метрика, расстояние, мера близости) между элементом выборки 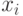 и точкой
и точкой 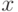 , в которой оценивается плотность, последовательность
, в которой оценивается плотность, последовательность 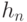 показателей размытости такова, что
показателей размытости такова, что  и
и 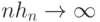 при
при 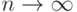 , а
, а 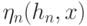 - нормирующий множитель, обеспечивающий выполнение условия нормировки (интеграл по всему пространству от непараметрической оценки плотности
- нормирующий множитель, обеспечивающий выполнение условия нормировки (интеграл по всему пространству от непараметрической оценки плотности  по мере
по мере  должен равняться 1). Ранее американские исследователи Парзен и Розенблатт использовали подобные статистики в случае
должен равняться 1). Ранее американские исследователи Парзен и Розенблатт использовали подобные статистики в случае 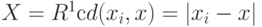 .
.
Введенные описанным образом ядерные оценки плотности - частный случай так называемых линейных оценок, также впервые предложенных в работе [31]. В теоретическом плане они выделяются тем, что удается получать результаты такого же типа, что в классическом одномерном случае, но, разумеется, с помощью совсем иного математического аппарата.
Свойства непараметрических ядерных оценок плотности. Рассмотрим выборку со значениями в некотором пространстве произвольного вида. В этом пространстве предполагаются заданными показатель различия 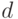 и мера
и мера 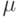 . Одна из основных идей рассматриваемого подхода состоит в том, чтобы согласовать их между собой. А именно, на их основе построим новый показатель различия
. Одна из основных идей рассматриваемого подхода состоит в том, чтобы согласовать их между собой. А именно, на их основе построим новый показатель различия 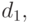 так называемый "естественный", в терминах которого проще формулируются свойства непараметрической оценки плотности. Для этого рассмотрим шары
так называемый "естественный", в терминах которого проще формулируются свойства непараметрической оценки плотности. Для этого рассмотрим шары 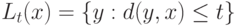 радиуса
радиуса 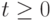 и их меры
и их меры 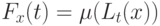 . Предположим, что
. Предположим, что 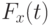 как функция t при фиксированном
как функция t при фиксированном 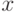 непрерывна и строго возрастает. Введем функцию
непрерывна и строго возрастает. Введем функцию 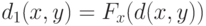 . Это - монотонное преобразование показателя различия или расстояния, а потому
. Это - монотонное преобразование показателя различия или расстояния, а потому 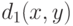 - также показатель различия (даже если
- также показатель различия (даже если 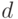 - метрика, для
- метрика, для 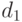 неравенство треугольника может быть не выполнено). Другими словами,
неравенство треугольника может быть не выполнено). Другими словами, 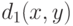 , как и
, как и 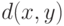 , можно рассматривать как показатель различия (меру близости) между
, можно рассматривать как показатель различия (меру близости) между 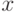 и
и 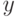 .
.
Для вновь введенного показателя различия 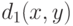 введем соответствующие шары
введем соответствующие шары 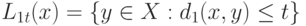 . Поскольку обратная функция
. Поскольку обратная функция 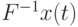 определена однозначно, то
определена однозначно, то 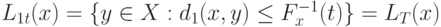 , где
, где 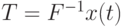 . Следовательно, справедлива цепочка равенств
. Следовательно, справедлива цепочка равенств 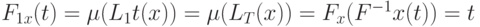 .
.
Переход от 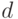 к
к 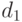 напоминает классическое преобразование, использованное Н.В. Смирновым при изучении непараметрических критериев согласия и однородности, а именно, преобразование
напоминает классическое преобразование, использованное Н.В. Смирновым при изучении непараметрических критериев согласия и однородности, а именно, преобразование 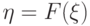 , переводящее случайную величину
, переводящее случайную величину 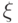 с непрерывной функцией распределения
с непрерывной функцией распределения  в случайную величину
в случайную величину 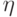 , равномерно распределенную на отрезке
, равномерно распределенную на отрезке ![[0,1]](/sites/default/files/tex_cache/63cf0c477385f522d8da2bcede82265f.png) . Оба рассматриваемых преобразования существенно упрощают дальнейшие рассмотрения. Преобразование
. Оба рассматриваемых преобразования существенно упрощают дальнейшие рассмотрения. Преобразование 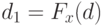 зависит от точки
зависит от точки 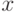 , что не влияет на дальнейшие рассуждения, поскольку ограничиваемся изучением сходимости в отдельно взятой точке.
, что не влияет на дальнейшие рассуждения, поскольку ограничиваемся изучением сходимости в отдельно взятой точке.
Функцию 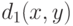 , для которой мера шара радиуса
, для которой мера шара радиуса 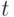 равна
равна 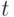 , называем в соответствии с работой [31] "естественным показателем различия" или "естественной метрикой". В случае конечномерного пространства
, называем в соответствии с работой [31] "естественным показателем различия" или "естественной метрикой". В случае конечномерного пространства 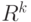 и евклидовой метрики
и евклидовой метрики 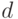 имеем
имеем  , где
, где 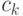 - объем шара единичного радиуса в
- объем шара единичного радиуса в 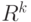 .
.
Поскольку можно записать, что
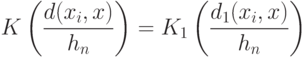
где

то переход от одного показателя различия к другому, т.е. от 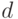 к
к 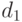 соответствует переходу от одной ядерной функции к другой, т.е. от
соответствует переходу от одной ядерной функции к другой, т.е. от 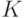 к
к 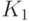 . Выгода от такого перехода заключается в том, что утверждения о поведении непараметрических оценок плотности приобретают более простую формулировку.
. Выгода от такого перехода заключается в том, что утверждения о поведении непараметрических оценок плотности приобретают более простую формулировку.
Теорема 5. Пусть 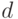 - естественная метрика, плотность
- естественная метрика, плотность 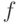 непрерывна в точке
непрерывна в точке 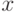 и ограничена на всем пространстве
и ограничена на всем пространстве 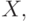 причем
причем 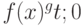 , ядерная функция
, ядерная функция 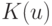 удовлетворяет простым условиям регулярности
удовлетворяет простым условиям регулярности
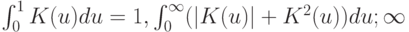
Тогда 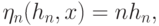 оценка
оценка  является состоятельной, т.е.
является состоятельной, т.е. 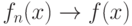 по вероятности при
по вероятности при 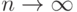 и, кроме того,
и, кроме того,
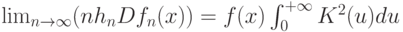
Теорема 5 доказывается методами, развитыми в работе [31]. Однако остается открытым вопрос о скорости сходимости ядерных оценок, в частности, о поведении величины 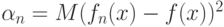 - среднего квадрата ошибки, и об оптимальном выборе показателей размытости
- среднего квадрата ошибки, и об оптимальном выборе показателей размытости 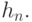 Для того, чтобы продвинуться в решении этого вопроса, введем новые понятия. Для случайного элемента
Для того, чтобы продвинуться в решении этого вопроса, введем новые понятия. Для случайного элемента 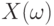 со значениями в
со значениями в 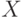 рассмотрим т.н. круговое распределение
рассмотрим т.н. круговое распределение  и круговую плотность
и круговую плотность  .
.
Теорема 6. Пусть ядерная функция 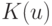 непрерывна и финитна, т.е. существует число
непрерывна и финитна, т.е. существует число 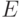 такое, что
такое, что 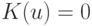 при
при 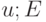 . Пусть круговая плотность является достаточно гладкой, т.е. допускает разложение
. Пусть круговая плотность является достаточно гладкой, т.е. допускает разложение
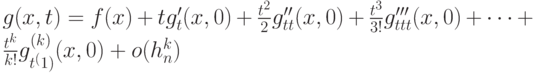
при некотором 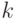 , причем остаточный член равномерно ограничен на
, причем остаточный член равномерно ограничен на ![[0,hE]](/sites/default/files/tex_cache/adb7abbf2b5bc15504c4edab8526af52.png) . Пусть
. Пусть
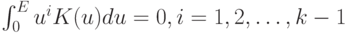
Тогда
![\alpha_n=[Mf_n(x)-f(x)]^2=h_n^{2k}\left(\int_0^E u^kK(u)du\right)^2(g_{t^(k)}^k(x,0))^2+\frac{f(x)}{nh_n}\int_0^EK^2(u)du+o\left(h_n^{2k}+\frac{1}{nh_n}\right)](/sites/default/files/tex_cache/f5409e11cf8942cea3e986c9621124b9.png)
Доказательство теоремы 6 проводится с помощью разработанной в статистике объектов нечисловой природы математической техники, образцы которой представлены, в частности, в работе [31]. Если коэффициенты при основных членах в правой части последней формулы не равны 0, то величина 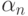 достигает минимума, равного
достигает минимума, равного 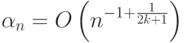 при
при 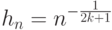 Эти выводы совпадают с классическими результатами, полученными ранее рядом авторов для весьма частного случая прямой
Эти выводы совпадают с классическими результатами, полученными ранее рядом авторов для весьма частного случая прямой  (см., например, монографию [32, с.316]). Заметим, что для уменьшения смещения оценки приходится применять знакопеременные ядра
(см., например, монографию [32, с.316]). Заметим, что для уменьшения смещения оценки приходится применять знакопеременные ядра 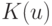 .
.
Непараметрические оценки плотности в конечных пространствах. В случае конечных пространств естественных метрик не существует. Однако можно получить аналоги теорем 5 и 6, переходя к пределу не только по объему выборки 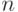 , но и по новому параметру дискретности
, но и по новому параметру дискретности 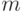 .
.
Рассмотрим некоторую последовательность  - конечных пространств. Пусть в
- конечных пространств. Пусть в 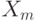 заданы показатели различия
заданы показатели различия 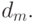 Будем использовать нормированные считающие меры
Будем использовать нормированные считающие меры 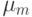 ставящие в соответствие каждому подмножеству
ставящие в соответствие каждому подмножеству  долю элементов всего пространства
долю элементов всего пространства  входящих в
входящих в  . Как и ранее, рассмотрим как функцию
. Как и ранее, рассмотрим как функцию 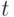 объем шара радиуса
объем шара радиуса 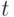 , т.е.
, т.е. 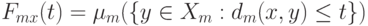 Введем аналог естественного показателя различия
Введем аналог естественного показателя различия 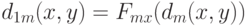 Наконец, рассмотрим аналоги преобразования Смирнова
Наконец, рассмотрим аналоги преобразования Смирнова 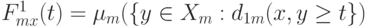 Функции
Функции 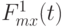 , в отличие от ситуации предыдущего раздела, уже не совпадают тождественно с
, в отличие от ситуации предыдущего раздела, уже не совпадают тождественно с 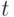 , они кусочно-постоянны и имеют скачки в некоторых точках
, они кусочно-постоянны и имеют скачки в некоторых точках 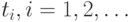 , причем в этих точках
, причем в этих точках 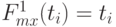
Теорема 7. Пусть точки скачков равномерно сближаются, т.е. 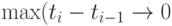 при
при 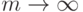 (другими словами,
(другими словами, 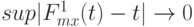 при
при 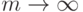 ). Тогда существует последовательность параметров дискретности mn такая, что при предельном переходе
). Тогда существует последовательность параметров дискретности mn такая, что при предельном переходе 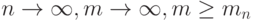 справедливы заключения теорем 5 и 6.
справедливы заключения теорем 5 и 6.
Пример 1. Пространство 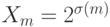 всех подмножеств конечного множества
всех подмножеств конечного множества 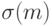 из m элементов допускает (см. монографию [3]) аксиоматическое введение метрики
из m элементов допускает (см. монографию [3]) аксиоматическое введение метрики  где
где  - символ симметрической разности множеств. Рассмотрим непараметрическую ядерную оценку плотности типа Парзена - Розенблатта
- символ симметрической разности множеств. Рассмотрим непараметрическую ядерную оценку плотности типа Парзена - Розенблатта
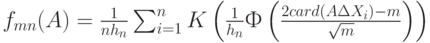
где 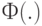 - функция нормального стандартного распределения. Можно показать, что эта оценка удовлетворяет условиям теоремы 7 с
- функция нормального стандартного распределения. Можно показать, что эта оценка удовлетворяет условиям теоремы 7 с 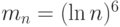
Пример 2. Рассмотрим пространство функций 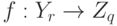 определенных на конечном множестве
определенных на конечном множестве  , со значениями в конечном множестве
, со значениями в конечном множестве 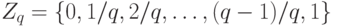 . Это пространство можно интерпретировать как пространство нечетких множеств (см. о нечетких множествах, напаример, монографии [3], [10]), а именно,
. Это пространство можно интерпретировать как пространство нечетких множеств (см. о нечетких множествах, напаример, монографии [3], [10]), а именно, 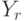 - носитель нечеткого множества, а
- носитель нечеткого множества, а 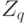 - множество значений функции принадлежности. Очевидно, число элементов пространства
- множество значений функции принадлежности. Очевидно, число элементов пространства 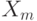 равно
равно 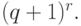 Будем использовать расстояние
Будем использовать расстояние 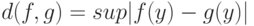 Непараметрическая оценка плотности имеет вид:
Непараметрическая оценка плотности имеет вид:
![f_{nm}=\frac{1}{nh_n}\sum_{i=1}^nK \left(\frac{[2sup_y|x(y)-x_i(y)|+\frac 1q]^r}{h_n(1+\frac 1q)^r} \right)](/sites/default/files/tex_cache/1a8c00b2d9e4b55d784d47ce81d7b38d.png)
Если 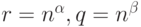 , то при
, то при 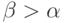 выполнены условия теоремы 7, а потому справедливы теоремы 5 и 6.
выполнены условия теоремы 7, а потому справедливы теоремы 5 и 6.
Пример 3. Рассматривая пространства ранжировок 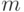 объектов, в качестве расстояния
объектов, в качестве расстояния 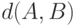 между ранжировками
между ранжировками 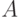 и
и 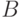 примем минимальное число инверсий, необходимых для перехода от
примем минимальное число инверсий, необходимых для перехода от 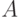 к
к 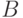 . Тогда
. Тогда 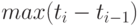 не стремится к 0 при
не стремится к 0 при 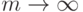 , условия теоремы 7 не выполнены.
, условия теоремы 7 не выполнены.
Пример 4. В прикладных работах наиболее распространенный пример объектов нечисловой природы - вектор разнотипных данных: реальный объект описывается вектором, часть координат которого - значения количественных признаков, а часть - качественных (номинальных и порядковых). Для пространств разнотипных признаков, т.е. декартовых произведений непрерывных и дискретных пространств, возможны различные постановки. Пусть, например, число градаций качественных признаков остается постоянным. Тогда непараметрическая оценка плотности сводится к произведению частоты попадания в точку в пространстве качественных признаков на классическую оценку Парзена-Розенблатта в пространстве количественных переменных. В общем случае расстояние 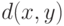 можно, например, рассматривать как сумму трех расстояний. А именно, евклидова расстояния
можно, например, рассматривать как сумму трех расстояний. А именно, евклидова расстояния 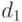 между количественными факторами, расстояния
между количественными факторами, расстояния  между номинальными признаками
между номинальными признаками 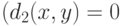 , если
, если 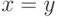 , и
, и 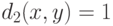 , если
, если  ) и расстояния
) и расстояния 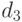 между порядковыми переменными (если x и y - номера градаций, то
между порядковыми переменными (если x и y - номера градаций, то 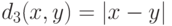 ). Наличие количественных факторов приводит к непрерывности и строгому возрастанию функции
). Наличие количественных факторов приводит к непрерывности и строгому возрастанию функции  , а потому для непараметрических оценок плотности в пространствах разнотипных признаков верны теоремы 5 - 6.
, а потому для непараметрических оценок плотности в пространствах разнотипных признаков верны теоремы 5 - 6.
Статистика объектов нечисловой природы как часть эконометрики продолжает бурно развиваться. Увеличивается количество ее практически полезных применений при анализе конкретных экономических данных - в маркетинговых исследованиях, контроллинге, при управлении предприятием и др.

