|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Многомерный статистический анализ
Пример оценивания по методу наименьших квадратов. Пусть даны  пар чисел
пар чисел 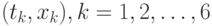 , представленных во втором и третьем столбцах табл.5.1. В соответствии с формулами (2) и (4) выше для вычисления оценок метода наименьших квадратов достаточно найти суммы выражений, представленных в четвертом и пятом столбцах табл.5.1.
, представленных во втором и третьем столбцах табл.5.1. В соответствии с формулами (2) и (4) выше для вычисления оценок метода наименьших квадратов достаточно найти суммы выражений, представленных в четвертом и пятом столбцах табл.5.1.
 |
 |
 |
 |
 |
 |
 |
 |
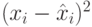 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 12 | 1 | 12 | 3.14 | 12.17 | -0.17 | 0.03 |
| 2 | 3 | 20 | 9 | 60 | 9,42 | 18,45 | 1,55 | 2,40 |
| 3 | 4 | 20 | 16 | 80 | 12,56 | 21,59 | -1,59 | 2,53 |
| 4 | 7 | 32 | 49 | 224 | 21,98 | 31,01 | 0,99 | 0,98 |
| 5 | 9 | 35 | 81 | 315 | 28,26 | 37,29 | -2,29 | 5,24 |
| 6 | 10 | 42 | 100 | 420 | 31,40 | 40,43 | 1,57 | 2,46 |
 |
34 | 161 | 256 | 1111 | 0,06 | 13,64 | ||
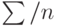 |
5,67 | 26,83 | 42,67 | 185,17 |
В соответствии с формулой (2) 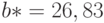 , а согласно формуле (4)
, а согласно формуле (4)
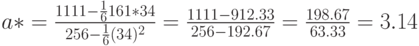
Следовательно, прогностическая формула имеет вид
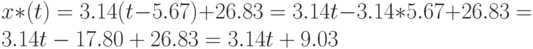
Следующий этап анализа данных - оценка точности приближения функции методом наименьших квадратов. Сначала рассматриваются т.н. восстановленные значения
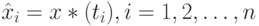
Это те значения, которые полученная в результате расчетов прогностическая функция принимает в тех точках, в которых известны истинные значения зависимой переменной 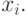
Вполне естественно сравнить восстановленные и истинные значения. Это и сделано в шестом - восьмом столбцах табл.5.1. Для простоты расчетов в шестом столбце представлены произведения  , седьмой отличается от шестого добавлением константы 9,03 и содержит восстановленные значения. Восьмой столбец - это разность третьего и седьмого.
, седьмой отличается от шестого добавлением константы 9,03 и содержит восстановленные значения. Восьмой столбец - это разность третьего и седьмого.
Непосредственный анализ восьмого столбца табл.1 показывает, что содержащиеся в нем числа сравнительно невелики по величине по сравнению с третьим столбцом (на порядок меньше по величине). Кроме того, знаки "+" и "-" чередуются. Эти два признака свидетельствуют о правильности расчетов. При использовании метода наименьших квадратов знаки не всегда чередуются. Однако если сначала идут только плюсы, а потом только минусы (или наоборот, сначала только минусы, а потом только плюсы), то это верный показатель того, что в вычислениях допущена ошибка.
Верно следующее утверждение.
Теорема.
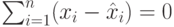
Доказательство этой теоремы оставляем читателю в качестве упражнения.
Однако сумма по восьмому столбцу дает 0,06, а не 0. Незначительное отличие от 0 связано с ошибками округления при вычислениях. Близость суммы значений зависимой переменной и суммы восстановленных значений - практический критерий правильности расчетов.
В последнем девятом столбце табл.5.1 приведены квадраты значений из восьмого столбца. Их сумма - это остаточная сумма квадратов 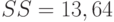 . В соответствии со сказанным выше оценками дисперсии погрешностей и их среднего квадратического отклонения являются
. В соответствии со сказанным выше оценками дисперсии погрешностей и их среднего квадратического отклонения являются
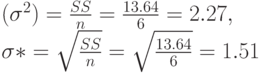
Рассмотрим распределения оценок параметров. Оценка 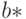 имеет асимптотически нормальное распределение с математическим ожиданием b и дисперсией, которая оценивается как
имеет асимптотически нормальное распределение с математическим ожиданием b и дисперсией, которая оценивается как 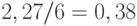 (здесь считаем, что 6 - "достаточно большое" число, что, конечно, можно оспаривать). Оценкой среднего квадратического отклонения является 0,615. Следовательно, при доверительной вероятности 0,95 доверительный интервал для параметра
(здесь считаем, что 6 - "достаточно большое" число, что, конечно, можно оспаривать). Оценкой среднего квадратического отклонения является 0,615. Следовательно, при доверительной вероятности 0,95 доверительный интервал для параметра  имеет вид
имеет вид 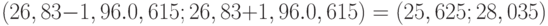 .
.
В формулах для дисперсий участвует величина
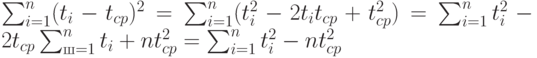
Подставив численные значения, получаем, что

Дисперсия для оценки 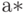 коэффициента при линейном члене прогностической функции оценивается как
коэффициента при линейном члене прогностической функции оценивается как 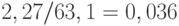 , а среднее квадратическое отклонение - как 0,19. Следовательно, при доверительной вероятности 0,95 доверительный интервал для параметра а имеет вид
, а среднее квадратическое отклонение - как 0,19. Следовательно, при доверительной вероятности 0,95 доверительный интервал для параметра а имеет вид 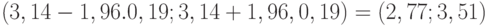 .
.
Прогностическая формула с учетом погрешности имеет вид (при доверительной вероятности 0,95)
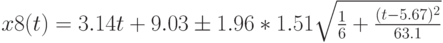
В этой записи сохранено происхождение различных составляющих. Упростим:
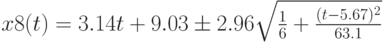
Например, при t = 12 эта формула дает
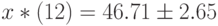
Следовательно, нижняя доверительная граница - это 44,06, а верхняя доверительная граница - это 49,336.
Насколько далеко можно прогнозировать? Обычный ответ таков - до тех пор, пока сохраняется тот стабильный комплекс условий, при котором справедлива рассматриваемая зависимость. Изобретатель метода наименьших квадратов Карл Гаусс исходил из задачи восстановления орбиты астероида (малой планеты) Церера. Движение подобных небесных тел может быть рассчитано на сотни лет. А вот параметры комет (например, срок возвращения) не поддаются столь точному расчету, поскольку за время пребывания в окрестности Солнца сильно меняется масса кометы. В социально-экономической области горизонты надежного прогнозирования еще менее определены. В частности, они сильно зависят от решений центральной власти.
Чтобы выявить роль погрешностей в прогностической формуле, рассмотрим формальный предельный переход  Тогда слагаемые 9,03; 1/6; 5,67 становятся бесконечно малыми, и
Тогда слагаемые 9,03; 1/6; 5,67 становятся бесконечно малыми, и

Таким образом, погрешности составляют около
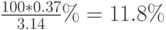
от тренда (математического ожидания) прогностической функции. В социально-экономических исследованиях подобные погрешности считаются вполне приемлемыми.
