|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Многомерный статистический анализ
Приведенные высказывания уже дают представление о больших расхождениях в понимании "естественной классификации". Этот термин следует признать нечетким, как, впрочем, и многие другие термины, как социально-экономические, научно-технические, так и используемые в обыденном языке. Нетрудно подробно обоснована нечеткость естественного языка и тот факт, что "мы мыслим нечетко", что однако не слишком мешает нам решать производственные и жизненные проблемы. Кажущееся рациональным требование выработать сначала строгие определения, а потом развивать науку - невыполнимо. Следовать ему - значит отвлекать силы от реальных задач. При системном подходе к теории классификации становится ясно, что строгие определения можно надеяться получить на последних этапах построения теории. Мы же сейчас находимся чаще всего на первых этапах. Поэтому, не давая определения понятиям "естественная классификация"и "естественная диагностика", обсудим, как проверить на "естественность" классификацию (набор диагностических классов), полученную расчетным путем.
Можно выделить два критерия "естественности", по поводу которых имеется относительное согласие:
А. Естественная классификация должна быть реальной, соответствующей действительному миру, лишенной внесенного исследователем субъективизма;
Б. Естественная классификация должна быть важной или с научной точки зрения (давать возможность прогноза, предсказания новых свойств, сжатия информации и т.д.), или с практической.
Пусть классификация проводится на основе информации об объектах, представленной в виде матрицы "объект-признак" или матрицы попарных расстояний (мер близости). Пусть алгоритм классификации дал разбиение на кластеры. Как можно получить доводы в пользу естественности этой классификации? Например, уверенность в том, что она - закон природы, может появиться только в результате длительного ее изучения и практического применения. Это соображение относится и к другим из перечисленных выше критериев, в частности к Б (важности). Сосредоточимся на критерии А (реальности).
Понятие "реальности" кластера требует специального обсуждения. (оно начато в работе [8]). Рассмотрим существо различий между понятиями "классификация" и "группировка". Пусть, к примеру, необходимо деревья, растущие в определенной местности, разбить на группы находящихся рядом друг с другом. Ясна интуитивная разница между несколькими отдельными рощами, далеко отстоящими друг от друга и разделенными полями, и сплошным лесом, разбитым просеками на квадраты с целью лесоустройства. Однако формально определить эту разницу столь же сложно, как определить понятие "куча зерен", чем занимались еще в Древней Греции (одно зерно не составляет кучи, два зерна не составляют кучи,…, если к тому, что не составляет кучи, добавить еще одно зерно, то куча не получится; значит - по принципу математической индукции - никакое количество зерен не составляет кучи; но ясно, что миллиард зерен - большая куча зерен - подсчитайте объем!).
Переформулируем сказанное в терминах "кластер-анализа" и "методов группировки". Выделенные с помощью первого подхода кластеры реальны, а потому могут рассматриваться как кандидаты в "естественные". Группировка дает "искусственные" классы, которые не могут быть "естественными".
Выборку из унимодального распределения можно, видимо, рассматривать как "естественный", "реальный" кластер. Применим к ней какой-либо алгоритм классификации ("средней связи", "ближайшего соседа" и т.п.). Он даст какое-то разбиение на классы, которые, разумеется, не являются "реальными", поскольку отражают прежде всего свойства алгоритма, а не исходных данных. Как отличить такую ситуацию от противоположной, когда имеются реальные кластеры и алгоритм классификации более или менее точно их выделяет? Как известно, "критерий истины - практика", но слишком много времени необходимо для применения подобного критерия. Поэтому представляет интерес критерий, оценивающий "реальность" выделяемых с помощью алгоритма классификации кластеров одновременно с его применением.
Такой показатель существует - это критерий устойчивости. Устойчивость - понятие широкое. Общая схема формулирования и изучения проблем устойчивости рассмотрена в "Проблемы устойчивости эконометрических процедур" . В частности, поскольку значения признаков всегда измеряются с погрешностями, то "реальное" разбиение должно быть устойчиво (т.е. не меняться или меняться слабо) при малых отклонениях исходных данных. Алгоритмов классификации существует бесконечно много, и "реальное" разбиение должно быть устойчиво по отношению к переходу к другому алгоритму. Другими словами, если "реальное" разбиение на диагностические классы возможно, то оно находится с помощью любого алгоритма автоматической классификация. Следовательно, критерием естественности классификации может служить совпадение результатов работы двух достаточно различающихся алгоритмов, например "ближайшего соседа" и "дальнего соседа".
Выше рассмотрены два типа "глобальных" критериев "естественности классификации", касающихся разбиения в целом. "Локальны"" критерии относятся к отдельным кластерам. Простейшая постановка такова: достаточно ли однородны два кластера (две совокупности) для их объединения:? Если объединение возможно, то кластеры не являются "естественными". Преимущество этой постановки в том, что она допускает применение статистических критериев однородности двух выборок. В одномерном случае (классификация по одному признаку) разработано большое число подобных критериев - Крамера-Уэлча, Смирнова, омега-квадрат (Лемана-Розенблатта), Вилкоксона, Ван-дер-Вардена, Лорда, Стьюдента и др. (см. "Статистический анализ числовых величин (непараметрическая статистика)" и справочник [1]). Имеются критерии и для многомерных данных. Для одного из видов объектов нечисловой природы - люсианов - статистические методы выделения "реальных" кластеров развиты в работе [9].
Что касается глобальных критериев, то для изучения устойчивости по отношению к малым отклонениям исходных данных естественно использовать метод статистических испытаний и проводить расчеты по "возмущенным" данным. Некоторые теоретические утверждения, касающиеся влияния "возмущений" на кластеры различных типов, получены в работе [8].
Опишем практический опыт реализации анализа устойчивости. Несколько алгоритмов классификации были применены к данным, полученным при проведении маркетинга образовательных услуг и приведенным в работе [10]. Для анализа данных были использованы широко известные алгоритмы "ближайшего соседа", "дальнего соседа" и алгоритм кластер-анализа из работы [11]. С содержательной точки зрения полученные разбиения отличались мало. Поэтому есть основания считать, что с помощью этих алгоритмов действительно выявлена "реальная" структура данных.
Идея устойчивости как критерия "реальности" иногда реализуется неадекватно. Так, для однопараметрических алгоритмов один из специалистов предлагал выделять разбиения, которым соответствуют наибольшие интервалы устойчивости по параметру, т.е. наибольшие приращения параметра между очередными объединениями кластеров. Для данных работы [10] это предложение не дало полезных результатов - были получены различные разбиения: три алгоритма - три разбиения. И с теоретической точки зрения предложение этого специалиста несостоятельно. Покажем это.
Действительно, рассмотрим алгоритм "ближайшего соседа", использующий меру близости  , и однопараметрическое семейство алгоритмов с мерой близости
, и однопараметрическое семейство алгоритмов с мерой близости 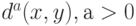 , также являющихся алгоритмами "ближайшего соседа". Тогда дендрограммы, полученные с помощью этих алгоритмов, совпадают при всех
, также являющихся алгоритмами "ближайшего соседа". Тогда дендрограммы, полученные с помощью этих алгоритмов, совпадают при всех  , поскольку при их реализации происходит лишь сравнение мер близости между объектами. Другими словами, дендрограмма, полученная с помощью алгоритма "ближайшего соседа", является адекватной в порядковой шкале (измерения меры близости
, поскольку при их реализации происходит лишь сравнение мер близости между объектами. Другими словами, дендрограмма, полученная с помощью алгоритма "ближайшего соседа", является адекватной в порядковой шкале (измерения меры близости  ), т.е. сохраняется при любом строго возрастающем преобразовании этой меры (см.
"Основы теории измерений"
). Однако выделенные по обсуждаемому методу "устойчивые разбиения" меняются. В частности, при достаточно большом а "наиболее объективным" в соответствии с предложением этого специалиста будет, как нетрудно показать, разбиение на два кластера! Таким образом, разбиение, выдвинутое им как "устойчивое", на самом деле оказывается весьма неустойчивым.
), т.е. сохраняется при любом строго возрастающем преобразовании этой меры (см.
"Основы теории измерений"
). Однако выделенные по обсуждаемому методу "устойчивые разбиения" меняются. В частности, при достаточно большом а "наиболее объективным" в соответствии с предложением этого специалиста будет, как нетрудно показать, разбиение на два кластера! Таким образом, разбиение, выдвинутое им как "устойчивое", на самом деле оказывается весьма неустойчивым.
Эконометрика классификации
Рассмотрим несколько конкретных эконометрических вопросов теории классификации.
Вероятностная теория кластер-анализа. Как и для прочих методов эконометрики и прикладной статистики, свойства алгоритмов кластер-анализа необходимо изучать на вероятностных моделях. Это касается, например, условий естественного объединения двух кластеров.
Вероятностные постановки нужно применять, в частности, при перенесении результатов, полученных по выборке, на генеральную совокупность. Вероятностная теория кластер-анализа и методов группировки различна для исходных данных типа таблиц "объект  признак" и матриц сходства. Для первых параметрическая вероятностно-статистическая теория называется "расщеплением смесей". Непараметрическая теория основана на непараметрических оценках плотностей вероятностей и их мод. Основные результаты, связанные с непараметрическими оценками плотности, обсуждаются ниже (
"Статистика нечисловых данных"
).
признак" и матриц сходства. Для первых параметрическая вероятностно-статистическая теория называется "расщеплением смесей". Непараметрическая теория основана на непараметрических оценках плотностей вероятностей и их мод. Основные результаты, связанные с непараметрическими оценками плотности, обсуждаются ниже (
"Статистика нечисловых данных"
).
Если исходные данные - матрица сходства 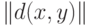 , то необходимо признать, что развитой вероятностно-статистической теории пока нет. Подходы к ее построению обсуждались в работе [8]. Одна из основных проблем - проверка "реальности" кластера, его объективного существования независимо от расчетов исследователя. Проблема "реальности" кластера давно обсуждается специалистами различных областей. Типичное рассуждение таково. Предположим, что результаты наблюдений можно рассматривать как выборку из некоторого распределения с монотонно убывающей плотностью при увеличении расстояния от некоторого центра. Примененный к подобным данным какой-либо алгоритм кластер-анализа порождает некоторое разбиение. Ясно, что оно - чисто формальное, поскольку выделенным таксонам (кластерам) не соответствуют никакие "реальные" классы. Другими словами, задача кластер-анализа не имеет решения, а алгоритм дает лишь группировку. При обработке реальных данных мы не знаем вида плотности. Проблема состоит в том, чтобы определить, каков результат работы алгоритма (реальные кластеры или формальные группы).
, то необходимо признать, что развитой вероятностно-статистической теории пока нет. Подходы к ее построению обсуждались в работе [8]. Одна из основных проблем - проверка "реальности" кластера, его объективного существования независимо от расчетов исследователя. Проблема "реальности" кластера давно обсуждается специалистами различных областей. Типичное рассуждение таково. Предположим, что результаты наблюдений можно рассматривать как выборку из некоторого распределения с монотонно убывающей плотностью при увеличении расстояния от некоторого центра. Примененный к подобным данным какой-либо алгоритм кластер-анализа порождает некоторое разбиение. Ясно, что оно - чисто формальное, поскольку выделенным таксонам (кластерам) не соответствуют никакие "реальные" классы. Другими словами, задача кластер-анализа не имеет решения, а алгоритм дает лишь группировку. При обработке реальных данных мы не знаем вида плотности. Проблема состоит в том, чтобы определить, каков результат работы алгоритма (реальные кластеры или формальные группы).
Частный случай этой проблемы - проверка обоснованности объединения двух кластеров, которые мы рассматриваем как два множества объектов, а именно, множества 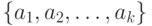 и
и 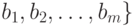 . Пусть, например, используется алгоритм типа "Дендрограмма". Естественной представляется следующая идея. Пусть есть две совокупности мер близости: одна - меры близости между объектами, лежащими внутри одного кластера, т.е.
. Пусть, например, используется алгоритм типа "Дендрограмма". Естественной представляется следующая идея. Пусть есть две совокупности мер близости: одна - меры близости между объектами, лежащими внутри одного кластера, т.е. 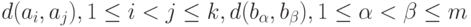 , и другая - меры близости между объектами, лежащими в разных кластерах, т.е.
, и другая - меры близости между объектами, лежащими в разных кластерах, т.е.  . Эти две совокупности мер близости предлагается рассматривать как независимые выборки и проверять гипотезу о совпадении их функций распределения. Если гипотеза не отвергается, объединение кластеров считается обоснованным; в противном случае - объединять нельзя, алгоритм прекращает работу.
. Эти две совокупности мер близости предлагается рассматривать как независимые выборки и проверять гипотезу о совпадении их функций распределения. Если гипотеза не отвергается, объединение кластеров считается обоснованным; в противном случае - объединять нельзя, алгоритм прекращает работу.
В рассматриваемом подходе есть две некорректности (см. также работу [8, разд.4]). Во-первых, меры близости не являются независимыми случайными величинами. Во-вторых, не учитывается, что объединяются не заранее фиксированные кластеры (с детерминированным составом), а полученные в результате работы некоторого алгоритма, и их состав (в частности, количество элементов) оказывается случайным От первой из этих некорректностей можно частично избавиться. Справедливо следующее утверждение.
Теорема 1. Пусть 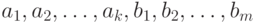 - независимые одинаково распределенные случайные величины (со значениями в произвольном пространстве). Пусть случайная величина
- независимые одинаково распределенные случайные величины (со значениями в произвольном пространстве). Пусть случайная величина  имеет все моменты. Тогда при
имеет все моменты. Тогда при 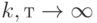 распределение статистики
распределение статистики
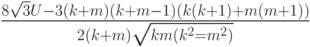
(где  - сумма рангов элементов первой выборки в объединенной выборке; первая выборка составлена из внутрикластерных расстояний (мер близости)
- сумма рангов элементов первой выборки в объединенной выборке; первая выборка составлена из внутрикластерных расстояний (мер близости)  , и
, и  , а вторая - из межкластерных расстояний
, а вторая - из межкластерных расстояний  сходится к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1.
сходится к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1.
На основе теоремы 1 очевидным образом формулируется правило проверки обоснованности объединения двух кластеров. Другими словами, мы проверяем статистическую гипотезу, согласно которой объединение двух кластеров образует однородную совокупность. Если величина  слишком мала, статистическая гипотеза однородности отклоняется (на заданном уровне значимости), и возможность объединения отбрасывается. Таким образом, хотя расстояния между объектами в кластерах зависимы, но эта зависимость слаба, и доказана математическая теорема о допустимости применения критерия Вилкоксона для проверки возможности объединения кластеров.
слишком мала, статистическая гипотеза однородности отклоняется (на заданном уровне значимости), и возможность объединения отбрасывается. Таким образом, хотя расстояния между объектами в кластерах зависимы, но эта зависимость слаба, и доказана математическая теорема о допустимости применения критерия Вилкоксона для проверки возможности объединения кластеров.
О вычислительной сходимости алгоритмов кластер-анализа. Алгоритмы кластер-анализа и группировки зачастую являются итерационными. Например, формулируется правило улучшения решения задачи кластер-анализа шаг за шагом, но момент остановки вычислений не обсуждается. Примером является известный алгоритм "Форель", в котором постепенно улучшается положение центра кластера. В этом алгоритме на каждом шагу строится шар определенного заранее радиуса, выделяются элементы кластеризуемой совокупности, попадающие в этот шар, и новый центр кластера строится как центр тяжести выделенных элементов. При анализе алгоритма "Форель" возникает проблема: завершится ли процесс улучшения положения центра кластера через конечное число шагов или же он может быть бесконечным. Она получила название "проблема остановки". Для широкого класса так называемых "эталонных алгоритмов" проблема остановки была решена в работе [8]: процесс улучшения остановится через конечное число шагов.
Отметим, что алгоритмы кластер-анализа могут быть модифицированы разнообразными способами. Например, описывая алгоритм "Форель" в стиле статистики объектов нечисловой природы, заметим, что вычисление центра тяжести для совокупности многомерных точек - это нахождение эмпирического среднего для меры близости, равной квадрату евклидова расстояния. Если взять более естественную меру близости - само евклидово расстояние, то получим алгоритм кластер-анализа "Медиана", отличающийся от "Форели" тем, что новый центр строится не с помощью средних арифметических координат элементов, попавших в кластер, а с помощью медиан.
