| Россия, г. Москва |
Обслуживание полнодоступной группы потребителей от группы с ограниченным числом партий товаров (формула Энгсета)
5.1. Постановка задачи
Определим три основных элемента математической модели (рис. 5.1):
Дано:
-
Основная система - рынок, который обслуживает
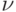 групп потребителей, к которым равнодоступны поступающие партии товаров.
групп потребителей, к которым равнодоступны поступающие партии товаров. -
На рынок поступает случайный примитивный поток n партий товаров с параметром
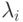 . При этом вероятность поступления новых партий числа в рассматриваемый момент времени будет зависеть от числа обслуженных (проданных) партий товаров.
. При этом вероятность поступления новых партий числа в рассматриваемый момент времени будет зависеть от числа обслуженных (проданных) партий товаров. Напомним ( "Математическая модель рынка" , раздел 1.2.1), что примитивным называется такой симметричный поток, параметр которого
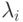 прямо пропорционален числу неприобретённых в данный момент партий товаров:
прямо пропорционален числу неприобретённых в данный момент партий товаров:
где
 - общее число партий товаров;
- общее число партий товаров;  - число проданных партий товаров;
- число проданных партий товаров;  - параметр потока группы партий в свободном состоянии -когда не продано ни одной группы товаров (при этом имеет место естественное предположение, что проданная партия товаров не может быть снова предложена для продажи).
- параметр потока группы партий в свободном состоянии -когда не продано ни одной группы товаров (при этом имеет место естественное предположение, что проданная партия товаров не может быть снова предложена для продажи).Примитивный поток характерен, для рынка с малым числом производителей (небольшой величиной предложения), когда каждая покупка (потребление) снижает величины предложения.
Как и прежде, будем предполагать, что длительность потребления, подчиняется показательному закону распределения с параметром
 :
: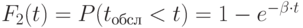
-
В качестве дисциплины обслуживания примем обслуживание с
явными потерями.
Требуется найти вероятность приобретения
 любых товаров из общего числа
любых товаров из общего числа 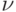 в фиксированный момент времени.
в фиксированный момент времени.
5.2. Вывод формулы Энгсета
Вспомним процесс рождения и гибели - частный случай Марковского процесса.

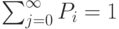
Рассмотрим систему в стационарном режиме. Определим 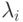 и
и 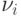 для рассматриваемой модели.
для рассматриваемой модели.
Обозначим через  вероятность поступления хотя бы одной партии товара от оставшейся группы товаров на отрезке
вероятность поступления хотя бы одной партии товара от оставшейся группы товаров на отрезке  при
при 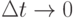 (параметр группы производителей). В состоянии системы xi из n групп товаров осталось
(параметр группы производителей). В состоянии системы xi из n групп товаров осталось 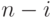 групп. Следовательно, вероятность поступления партии товара в состоянии системы
групп. Следовательно, вероятность поступления партии товара в состоянии системы  за
за  :
:
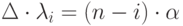 , то есть
, то есть 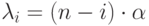 ;
;
где  - параметр группы оставшихся производителей.
- параметр группы оставшихся производителей.
Вероятность освобождения одной группы за отрезок  равна:
равна:

В состоянии  занято
занято  групп потребителей. Вероятность освобождения одной группы потребителей (или первой, или второй, …, или
групп потребителей. Вероятность освобождения одной группы потребителей (или первой, или второй, …, или  -той) равна:
-той) равна:
 , то есть
, то есть 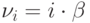 .
.
Для такой модели вероятность перехода в следующее состояние зависит
от предыдущего состояния, но не зависит от того, как система оказалась в этом предыдущем состоянии, то есть процесс Марковский.
Подставив в выражение для 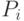 вместо
вместо 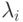 и
и 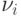 их значения
их значения  и
и  , получим:
, получим:
![P_i=\frac{\lambda _1 \cdot \lambda _2 \cdot \lambda _3 \cdot … \lambda _{i-1}}{\nu _1 \cdot \nu _2 \cdot \nu _3 \cdot … \nu _i}\cdot P_0=\frac{N\cdot \alpha \cdot (N-1)\cdot \alpha \cdot … \cdot [N-(i-1)]}{\beta \cdot 2\beta \cdot 3\beta \cdot … \cdot i\cdot \beta}\cdot P_0=…=\frac{N\cdot \alpha \cdot (N-1)\cdot \alpha \cdot … \cdot [N-(i-1)]}{i!}\cdot \frac{\alpha ^i}{\beta ^i}\cdot P_0=C_N^i \cdot (\frac{\alpha}{\beta})^i \cdot P_0](/sites/default/files/tex_cache/394bf23367c35eed69dd5a553771b218.png) ,
,
где 
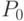 определим из условия
определим из условия 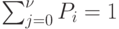
В теории массового обслуживания часто пользуются следующим приёмом: для простоты записи выражений длительность занятия одной группы потребителей выражают в единицах средней длительности потребления, то есть принимают 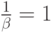 .
.
Это изменяет масштаб, но результаты от этого не изменяются.
С учётом сказанного: 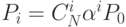

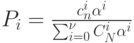 - распределение Энгсета (немецкий учёный, 1918г.).
- распределение Энгсета (немецкий учёный, 1918г.).
Огибающая распределения Энгсета похожа на огибающую распределения Эрланга.