НОУ ИНТУИТ | Рынок как система обслуживания случайных потоков. Лекция 4: Рынок как система с ожиданием

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 26.10.2016 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 23 студентам

| Поделиться |

Поддержать программу

4.6. Вероятность очереди (вероятность наличия в очереди хотя бы одной партии товаров)

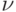В состоянии системы $x_{\nu }$ все $\nu$ групп потребителей заняты, но очереди нет.

В состоянии 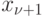$x_{\nu+1}$ заняты все 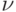$\nu$ линий и одна группа товаров стоит в очереди.

В состоянии 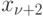$x_{\nu+2}$ стоят в очереди 2 группы товаров и так далее...

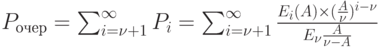
$P_{очер}=\sum_{i=\nu +1}^{\infty }P_i=\sum_{i=\nu +1}^{\infty }\frac{E_i (A) \times (\frac{A}{\nu })^{i-\nu }}{E_{\nu }\frac{A}{\nu -A}}$

В этом выражении обозначим 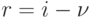$r=i-\nu$ :

$\sum\nolimits_{r=1}^{\infty }(\frac{A}{\nu})^r=(\frac{A}{\nu })[1+\frac{A}{\nu }+(\frac{A}{\nu })^2+…]=\frac{A}{\nu }\frac{1}{1-\frac{A}{\nu }}$

Вероятность очереди:

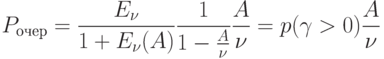$P_{очер}=\frac{E_{\nu }}{1+E_{\nu }(A)}\frac{1}{1-\frac{A}{\nu}}\frac{A}{\nu}=p(\gamma > 0)\frac{A}{\nu }$

( 4.14)

4.7. Средняя длина очереди или среднее число задержанных партий товаров

Математическое ожидание числа задержанных партий товаров

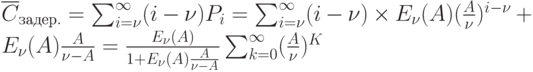
$\overline {C}_{задер.}= \sum\nolimits_{i=\nu }^{\infty }(i-\nu )P_i= \sum\nolimits_{i=\nu }^{\infty }(i-\nu ) \times E_{\nu }(A)(\frac{A}{\nu })^{i-\nu }+E_{\nu }(A)\frac{A}{\nu -A}=\frac{E_{\nu }(A)}{1+E_{\nu }(A)\frac{A}{\nu -A}} \sum\nolimits_{k=0}^{\infty}(\frac{A}{\nu })^K$

Заменим 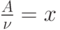$\frac{A}{\nu }=x$ и воспользуемся формулой $\frac{d}{dx}x^k=kx^{k-1}$

Число задержанных партий товаров будет:

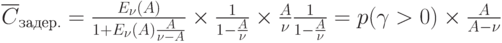
$\overline {C}_{задер.}=\frac{E_{\nu }(A)}{1+E_{\nu }(A)\frac{A}{\nu -A}}\times \frac{1}{1-\frac{A}{\nu }}\times \frac{A}{\nu }\frac{1}{1-\frac{A}{\nu }}=p(\gamma > 0)\times \frac{A}{A-\nu }$

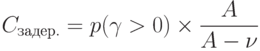$C_{задер.}=p(\gamma > 0)\times \frac{A}{A-\nu }$

( 4.15)

Таким образом, для оценки качества работы систем с ожиданием мы получили формулы (табл. 4.1).

Таблица 4.1. Формулы для расчета системы с ожиданием
$P(\gamma > 0)=E_{\nu }(A)\frac{\nu }{(\nu -A)+AE_{\nu }(A)}$	Вторая формула Эрланга (вероятность того, что время ожидания больше нуля- то есть вероятность очереди)
$p(\gamma > t)= p(\gamma > 0)e^{(\lambda - \nu )t}$	Вероятность того, что время ожидания поступившего вызова больше .
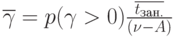$\overline {\gamma}=p(\gamma > 0)\frac{\overline {t_{зан.}}}{(\nu -A)}$	Среднее время ожидания для партий товаров, поступающих на рынок.
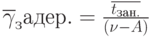$\overline {\gamma}_задер.=\frac{\overline {t_{зан.}}}{(\nu -A)}$	Среднее время ожидания товаров, находящихся в очереди.
$P_{очер}= p(\gamma > 0)\frac{A}{\nu }$	Вероятность наличия в очереди хотя бы одной партии товаров вероятность очереди.
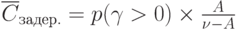$\overline {C}_{задер.}= p(\gamma > 0)\times \frac{A}{\nu -A}$	Средняя длина очереди (среднее число задержанных партий товаров)