Теория игр

Принцип оптимальности в теории игр

Каждый игрок должен стремиться не вообще к ситуации, в которой значение функции выигрыша максимально или минимально, а прежде всего к такой ситуации, которая может сложиться в процессе игры. Чтобы ситуация могла быть осуществимой, в ней одновременно должны достигаться приемлемые результаты как для игрока I, так и для игрока II. Ситуации, обладающие этим свойством, называются ситуациями равновесия . Именно они могут складываться в результате разумного выбора игроками своих стратегий. При выявлении ситуации равновесия необходимо прежде всего проанализировать последовательно каждую стратегию игрока I с точки зрения наиболее неблагоприятного для него исхода при выборе игроком II одной из своих стратегий. Для этого в - строке матрицы отыскивается минимальное значение выигрыша. Обозначим его 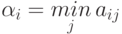, где знаком 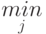(минимум по ) обозначена операция отыскания минимального из значений функции выигрыша при всех возможных .

Числа 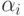, которые записаны рядом с матрицей в виде добавочного столбца, характеризуют минимальные выигрыши игрока I с учетом разумных действий игрока II. Поэтому игрок I должен выбрать свою стратегию так, чтобы максимизировать свой минимальный выигрыш, то есть он должен остановиться на той стратегии, для которой число 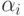является максимальным. Обозначим максимальное значение 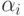через 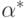, то есть

.

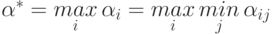Величина 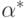называется нижним значением игры или максимином, а соответствующая ей стратегия игрока I – максиминной стратегией .

Очевидно, что при выборе наиболее осторожной максиминной стратегии игрок I обеспечивает себе (независимо от поведения противника) гарантированный выигрыш не менее .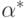

Далее проанализируем каждую стратегию игрока II с точки зрения наиболее неблагоприятного для него исхода при выборе игроком I одной из своих стратегий. В результате этого найдем максимальные значения проигрыша, которые обозначим

,

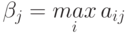где знаком 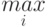(максимум по ) обозначено максимальное значение функции выигрыша при всех возможных .

Числа 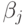, которые записаны под матрицей в виде добавочной строки, характеризуют максимальные проигрыши игрока II с учетом разумных действий игрока I. Поэтому игрок II должен выбрать свою стратегию так, чтобы минимизировать свой максимальный проигрыш. Для этого он должен остановиться на той стратегии, при которой число 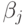будет минимальным. Обозначим минимальное значение 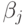через 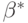, то есть

.

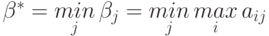Величина 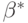называется верхним значением игры или минимаксом, а соответствующая ей стратегия игрока II – минимаксной стратегией .

Очевидно, что при выборе наиболее осторожной минимаксной стратегии игрок II не дает возможности ни при каких обстоятельствах игроку I выиграть больше, чем .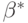

Следовательно, если оба игрока ведут себя разумно, то выигрыш игрока I должен быть не меньше, чем максимин, и не больше, чем минимакс, то есть:

( 8.1)

В некоторых играх выражение 7.1. превращается в равенство, то есть при определенных условиях может достигаться равенство максимина и минимакса, а именно:

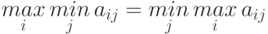( 8.2)

Необходимым и достаточным условием выполнения равенства 7.2. является существование седловой точки. 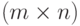матрицы. Термин "седловая точка" заимствован из геометрии. Однако наличие седловой точки в геометрии рассматривается в локальном, а в теории игр – в глобальном плане. То есть, декларируется существование пары целых чисел 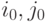, для которых 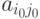оказывается одновременно минимумом своей строки и максимумом своего столбца. Поэтому игрок I, применяя максиминную стратегию 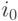, гарантирует себе выигрыш 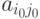, а игрок II, применяя минимаксную стратегию , не дает ему выиграть больше, чем .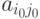

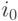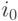Следовательно, для игрока I лучше всего выбирать стратегию , а для игрока II — . Согласно этому стратегии и называются оптимальными, а гарантированный выигрыш 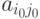игрока I – значением игры, которое обозначают через .

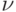Совокупность оптимальных стратегий называется решением игры .

Принцип оптимальности, лежащий в основе выбора игроками своих стратегий, называется принципом минимакса . В соответствии с этим принципом (или минимаксным критерием разумности поведения ) каждый способ действия оценивается по наихудшему для него исходу и оптимальным является способ, приводящий к наилучшему из наихудших результатов.

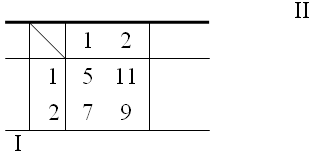
Рассмотрим матрицу игры.

Так, матрица имеет седловую точку 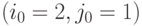, так как цифра 7 является минимумом второй строки и максимумом первого столбца. Следовательно, оптимальной стратегией игрока I является максиминная 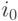, а игрока II – минимаксная 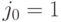. Значение игры .

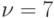Выбрав свою оптимальную стратегию, игрок I может быть уверен, что он получит по меньшей мере 7, а игрок II, выбрав свою оптимальную стратегию, не допустит, чтобы игрок I получил больше 7. Эти стратегии и составляют решение игры с седловой точкой.

Решение игры с седловой точкой обладает таким свойством: если игроки придерживаются своих оптимальных стратегий, то выигрыш равен значению игры. Если один из игроков придерживается своей оптимальной стратегии, а другой отклоняется от нее, то он только теряет в игре и ни в коем случае не может увеличить свой выигрыш. При этом наличие у любого игрока сведений о том, что другой избрал свою оптимальную стратегию, не служит основанием для выбора какой-либо иной, кроме оптимальной (минимаксной или максиминной), стратегии. Пара оптимальных стратегий в игре с седловой точкой создает ситуацию равновесия, и любое отклонение от оптимальной стратегии приводит игрока, применяющего неоптимальную стратегию, к невыгодным последствиям. Так, для рассматриваемой игры наличие информации у игрока 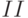о том, что игрок I выбрал оптимальную стратегию 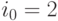, не влияет на выбор им своей оптимальной стратегии 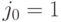. В противном случае игрок II даст возможность игроку I выиграть 9 вместо 7.

Смешанные стратегии. Наличие седловой точки определяет довольно простой способ выбора оптимальных стратегий, который вытекает из равенства 7.2. Однако равенство 7.2. справедливо не для всякой матрицы.

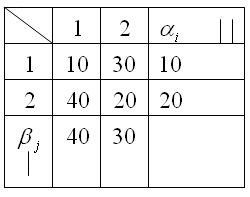
Пусть дана следующая матрица игры.

Из анализа этой матрицы видно, что максиминная стратегия игрока I гарантирует ему выигрыш не менее 20, а минимаксная стратегия игрока II — проигрыш не более 30. Однако, если игрок II будет придерживаться стратегии 2, игроку I выгодно отклониться от своей максиминной стратегии 2, то есть выбрать стратегию 1 и повысить выигрыш до 30. Тогда игроку I целесообразно выбрать стратегию не 2, а 1 и уменьшить выигрыш игрока I до 10. Но в свою очередь игрок I, выбирая 2, может увеличить выигрыш до 40, и так далее.

Оказывается, игрок I может добиться выигрыша более 20, а игрок II – проигрыша менее 30. Это следовало ожидать, так как принцип минимакса в этом случае обусловил область неопределенности выигрыша и проигрыша в пределах от 20 до 30. Каждый игрок поэтому получил шансы улучшить свое положение путем чередования всех стратегий.

Выбор каждым игроком своей чистой стратегии с некоторой заранее заданной вероятностью является не чем иным, как одним из планов проведения игры, то есть определенной стратегией. Для отличия стратегий такого вида от первоначально заданных стратегий их называют смешанными стратегиями, а первоначально заданные (то есть строки или столбцы матрицы) – чистыми стратегиями .

Смешанные стратегии обозначаются следующим образом:

,

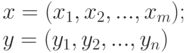где — вероятность выбора игроком I - чистой стратегии;

— вероятность выбора игроком II - чистой стратегии;

— число чистых стратегий игрока I;

— число чистых стратегий игрока II.

Очевидно, что 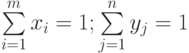, и каждая чистая стратегия является смешанной стратегией, в которой все стратегии, кроме одной, имеют вероятности, равные нулю, а данная – вероятность, равная единице.