Базовые идеи и методы теории вероятностей

Задачи

Задача о наилучшем выборе. Предположим, что имеется некоторая совокупность из предметов, сравнивая которые, наблюдатель может сказать, который лучше или хуже, а задача состоит в том, чтобы выбрать предмет как можно лучше. Предположим, что эта задача осложняется следующим обстоятельством: осмотрев и отвергнув некоторый предмет, нельзя к нему возвращаться. Тогда, в частности, можно случайно отвергнуть абсолютно наилучший предмет в надежде найти еще более лучший при дальнейшем осмотре (представьте себе, например. разборчивую невесту, которая либо принимает предложение сватающегося жениха – и тогда на этом выбор заканчивается, либо отвергает его – и тогда он безвозвратно потерян для невесты).

Рассмотрим одно естественное правило выбора: не останавливаться на том предмете, который хуже какого-нибудь уже ранее осмотренного предмета. Будем считать, что наблюдатель руководствуется этим правилом, так что при последовательном осмотре имеющихся предметов он может сразу выбрать первый из них ( и на этом процесс выбора закончится); если он этого не сделал, то он продолжает осмотр до тех пор, пока на каком-то шаге не обнаружится предмет, который будет лучше всех осмотренных ранее. Наблюдатель может выбрать этот наилучший среди осмотренных предметов (и на этом процесс выбора заканчивается), а может продолжить осмотр в надежде найти еще лучше, и так далее.

Конечно, при этом не исключено, что на самом деле будет отвергнут абсолютно наилучший предмет, и тогда вообще ничего не будет выбрано. Но если число имеющихся предметов велико, то едва ли кто-нибудь согласится взять первый попавшийся предмет, не испытав счастья найти что-нибудь получше.

Предположим, что следуя описанному правилу, наблюдатель сделает выбор, остановившись на -м осмотренном предмете, то есть последний из осмотренных предметов оказался лучше всех предшествующих и на него-то и пал выбор. Какова вероятность того, что этот выбранный предмет является наилучшим среди всей совокупности как осмотренных, так и еще не осмотренных предметов?

Обозначим как событие, состоящее в том, что среди осмотренных предметов последний оказался наилучшим, Наблюдателю известно о том, что событие произошло. Обозначим как событие, состоящее в том, что -й по счету предмет является наилучшим среди всех имеющихся предметов. Вопрос касается условной вероятности 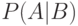события при условии наступления события . Эта условная вероятность 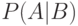находится по формуле 2.4. , так что для ответа на поставленный вопрос нужно найти вероятности событий и 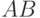. 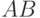Очевидно, событие содержится в и пересечение совпадает с самим событием . Описанные условия выбора таковы, что следует считать все возможные расположения предметов равновероятными. Вероятность события совпадает с вероятностью того, что при случайной перестановке отличимых друг от друга элементов (они отличаются по качеству) на фиксированном -м месте окажется наилучший из этих элементов. Такая вероятность равна 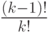, где ! — число перестановок из 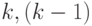! — число перестановок из элементов, совместимых с тем условием, что на 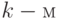месте зафиксирован наилучший элемент. Итак,

.

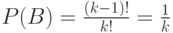Совершенно аналогично отыскивается вероятность события , которая совпадает с вероятностью того, что при случайной перестановке отличимых друг от друга элементов на фиксированном -м месте окажется вполне определенный элемент – наилучший предмет из всей имеющейся совокупности предметов. Таким образом,

,

и искомая условная вероятно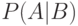сть есть

.

Задача о лотерейных билетах. Сколько нужно купить лотерейных билетов, чтобы вероятность выигрыша была не меньшей, чем ?

Пусть общее количество лотерейных билетов равно и — общее количество выигрышей. Тогда вероятность того, что купленный лотерейный билет окажется из числа выигрышных билетов, равна . Приобретение каждого отдельного билета можно рассматривать как отдельное испытание с вероятностью "успеха" в серии из независимых испытаний ( — число купленных билетов). Если считать, что вероятность мала, как это обычно бывает, а заданная вероятность сравнительно велика, то ясно, что нужно купить довольно большое число лотерейных билетов, чтобы вероятность хотя бы одного выигрыша была не меньше . Поэтому случайное число выигрышных билетов приблизительно распределено по закону Пуассона, то есть вероятность того, что среди купленных билетов окажется равно выигрышных, есть

,

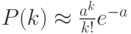где . Вероятность того, что хотя бы один из билетов будет выигрышным, есть , так что число нужно определить как наименьшее целое число, для которого

.
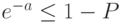