Проект "Выпуклая оболочка"
Аналитическая геометрия и программирование
В предыдущей секции мы столкнулись с необходимостью реализовать в классе R2Point ряд методов, которые позволяли бы вычислять расстояния между точками, сравнивать их на совпадение, выяснять, лежат ли три точки на одной прямой и не находится ли некоторая точка на прямой между двумя другими. Для реализации класса Polygon необходимо также уметь вычислять площадь треугольника и находить все освещенные ребра многоугольника. Решение задач на модификацию эталонного проекта потребует реализации еще целого ряда методов, связанных с различными геометрическими характеристиками.
Ряд фактов из аналитической геометрии и векторной алгебры являются необходимой базой для решения сформулированных задач, однако только знание элементов вычислительной геометрии позволяет получить достаточно эффективные решения. Простейшим примером может служить задача вычисления площади треугольника по известным координатам его вершин. Известная из средней школы формула Герона
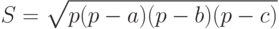
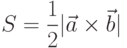
Большую часть методов, о которых будет идти речь в текущей секции, целесообразно реализовать в виде методов класса (статических методов). Напомним, что такой метод не получает в качестве неявного аргумента конкретный экземпляр класса, и не может использовать ключевое слово this.
Расстояние  между двумя точками на плоскости можно посчитать
по известной
формуле
между двумя точками на плоскости можно посчитать
по известной
формуле 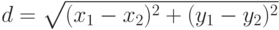 , которая и
используется в
реализации метода dist. Два объекта типа R2Point соответствуют
совпадающим точкам плоскости тогда и только тогда, когда попарно равны их
координаты, что позволяет реализовать метод equal.
, которая и
используется в
реализации метода dist. Два объекта типа R2Point соответствуют
совпадающим точкам плоскости тогда и только тогда, когда попарно равны их
координаты, что позволяет реализовать метод equal.
public static double dist(R2Point a, R2Point b) {
return Math.sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
public static boolean equal(R2Point a, R2Point b) {
return a.x==b.x && a.y==b.y;
}
public static double area(R2Point a, R2Point b, R2Point c) {
return 0.5*((a.x-c.x)*(b.y-c.y)-(a.y-c.y)*(b.x-c.x));
}Для вычисления площади треугольника в методе area применена уже
цитированная выше формула, основанная на следующем факте из векторной алгебры:
модуль векторного произведения двух векторов равен площади параллелограмма,
натянутого на эти вектора. Напомним, что векторным произведением 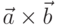 двух
векторов
двух
векторов 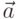 и
и 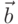 называется вектор
называется вектор  , перпендикулярный
векторам
, перпендикулярный
векторам 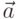 и
и 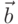 , такой, что
, такой, что  , где
, где  — угол между векторами
— угол между векторами 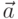 и
и 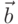 . Одно из
двух возможных направлений вектора
. Одно из
двух возможных направлений вектора 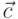 при этом определяется
по правилу буравчика
(при повороте ручки по направлению от
при этом определяется
по правилу буравчика
(при повороте ручки по направлению от 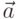 к
к 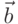 буравчик перемещается
по направлению вектора
буравчик перемещается
по направлению вектора 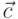 ).
).
Часто полезно использовать запись этого определения в координатах.
Если 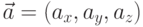 , а
, а 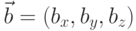 , то координаты
вектора
, то координаты
вектора 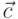 находятся по формуле
находятся по формуле
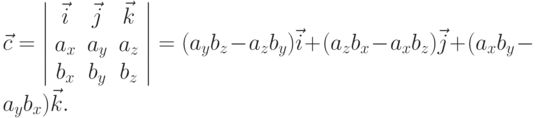
В том случае, когда вектора 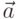 и
и 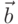 расположены на плоскости, их
векторное произведение имеет единственную не нулевую компоненту, вычисление
которой и реализовано в методе area. Обратите внимание на то, что так
вычисленная площадь является ориентированной, то есть может быть
отрицательной.
расположены на плоскости, их
векторное произведение имеет единственную не нулевую компоненту, вычисление
которой и реализовано в методе area. Обратите внимание на то, что так
вычисленная площадь является ориентированной, то есть может быть
отрицательной.
Выяснение того факта, лежат ли три точки на одной прямой, сводится к
вычислению площади треугольника и сравнению ее с нулем, а для того, чтобы
точка  прямой располагалась на отрезке
прямой располагалась на отрезке ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) этой
же прямой,
необходимо и достаточно принадлежности проекций этой точки проекциям на
оси координат отрезка
этой
же прямой,
необходимо и достаточно принадлежности проекций этой точки проекциям на
оси координат отрезка ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Вот как выглядит программная
реализация этих
идей.
. Вот как выглядит программная
реализация этих
идей.
public static boolean isTriangle(R2Point a, R2Point b, R2Point c) {
return area(a, b, c) != 0.0;
}
public boolean inside(R2Point a, R2Point b) {
return (a.x <= x && x <= b.x || a.x >= x && x >= b.x) &&
(a.y <= y && y <= b.y || a.y >= y && y >= b.y);
}Перед тем, как реализовать метод light, позволяющий выяснить,
освещено ли
ребро ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) выпуклой оболочки из точки
выпуклой оболочки из точки  , дадим
строгое определение
освещенности.
, дадим
строгое определение
освещенности.
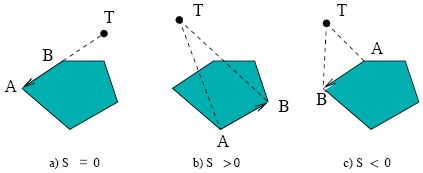
Определение 11.3.
Ребро ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) называется освещенным из точки
называется освещенным из точки  ,
если ориентированная
площадь треугольника, образованного точками
,
если ориентированная
площадь треугольника, образованного точками  ,
,  и
и  отрицательна,
либо если точка
отрицательна,
либо если точка  расположена на прямой, проходящей через
точки
расположена на прямой, проходящей через
точки  и
и  , вне отрезка
, вне отрезка ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
Заметим, что при таком формальном определении понятия освещенности никакое ребро многоугольника не освещено ни из одной точки внутри или на границе многоугольника, что хорошо видно на рисунке рис. 11.5.
public boolean light(R2Point a, R2Point b) {
double s = area(a, b, this);
return s < 0.0 || ( s == 0.0 && ! inside(a, b));
}В заключение этой секции рассмотрим более сложный вопрос — покажем, как можно наиболее эффективно выяснить, пересекаются ли два отрезка на плоскости, заданные координатами четырех их граничных точек.
На первом шаге решения этой задачи необходимо выяснить, пересекаются ли ограничивающие прямоугольники ( bounding boxes ) этих отрезков. Ограничивающий прямоугольник — это минимальный прямоугольник со сторонами, параллельными осям координат, содержащий отрезок.
Пусть координаты граничных точек первого отрезка  равны
равны  и
и 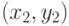 , а второго
, а второго  —
— 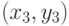 и
и 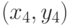 . Тогда координаты
левого нижнего угла ограничивающего прямоугольника первого отрезка будут
равны
. Тогда координаты
левого нижнего угла ограничивающего прямоугольника первого отрезка будут
равны 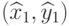 , а правого верхнего угла —
, а правого верхнего угла — 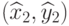 , где
, где 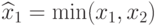 ,
,  ,
, 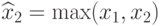 и
и 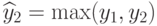 . Аналогично определяются координаты
. Аналогично определяются координаты 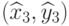 и
и 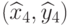 левого
нижнего и правого верхнего углов ограничивающего прямоугольника второго
отрезка.
левого
нижнего и правого верхнего углов ограничивающего прямоугольника второго
отрезка.
Ограничивающие прямоугольники пересекаются тогда и только тогда, когда
пересекаются их проекции на каждую из двух осей, что сводится к
истинности следующего предиката 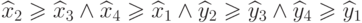 .
.
Если ограничивающие прямоугольники пересекаются, то необходимо дальнейшее исследование. Для начала можно выяснить, пересекает ли каждый из данных отрезков прямую, содержащую другой отрезок. Отрезок пересекает прямую, если его концы лежат по разные стороны от нее или если один из концов лежит на прямой.
Можно доказать (это рекомендуется сделать самостоятельно), что два отрезка пересекаются тогда и только тогда, когда пересекаются их ограничивающие прямоугольники и, кроме того, каждый из них пересекается с прямой, содержащей другой отрезок.
Проверка факта пересечения отрезка с прямой осуществляется с помощью
векторных произведений следующим образом. Точки 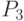 и
и 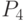 лежат по разные
стороны от прямой
лежат по разные
стороны от прямой  , если векторы
, если векторы 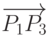 и
и  имеют различную ориентацию относительно
вектора
имеют различную ориентацию относительно
вектора  , то есть, если знаки векторных
произведений
, то есть, если знаки векторных
произведений 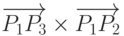 и
и 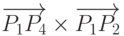 различны.
различны.
Таким образом, отрезки  и
и  пересекаются тогда и только тогда, когда
одновременно выполняются следующие три условия:
пересекаются тогда и только тогда, когда
одновременно выполняются следующие три условия:
1) пересекаются ограничивающие их прямоугольники;
2) 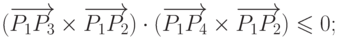
3) 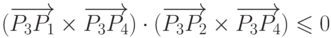 .
.
Более подробное изложение решения этой и ряда других подобных задач может быть найдено в разделе "Вычислительная геометрия" книги [8].