Проект "Выпуклая оболочка"
Задачи для самостоятельного решения
Задача 11.5. Создайте аплет, изображающий в окне стандартный прямоугольник (со сторонами,
параллельными осям координат), заштрихованный под углом 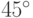 .
.
Задача 11.6. Создайте аплет, изображающий в окне границу объединения двух стандартных прямоугольников (со сторонами, параллельными осям координат), координаты углов которых предварительно вводятся с помощью методов класса Xterm
Задача 11.7. Создайте аплет, изображающий в окне размером 600x600 график функции,
заданной параметрически:  ,
, 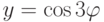 .
.
Задача 11.8. Создайте аплет, изображающий в окне размером 600x600 линии уровня
функции 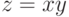 .
.
Задача 11.9. Создайте аплет, изображающий в окне размером 600x600 траекторию движения
шара с начальными координатами 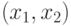 и скоростью
и скоростью 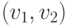 в
квадратном билльярде со стороной единичной длины.
в
квадратном билльярде со стороной единичной длины.
Задача 11.10. Модифицируйте текст эталонного проекта "Выпуклая оболочка" так, чтобы индуктивно определить:
a) среднее арифметическое значений функции 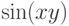 в вершинах выпуклой
оболочки;
в вершинах выпуклой
оболочки;
b) максимальное значение функции 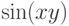 в серединах сторон выпуклой
оболочки;
в серединах сторон выпуклой
оболочки;
c) мощность множества пересечения границы выпуклой оболочки с полосой 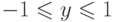 ;
;
d) площадь части выпуклой оболочки, расположенной внутри кольца 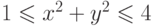 ;
;
e) периметр части выпуклой оболочки, расположенной внутри кольца 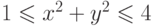 ;
;
f) количество ребер выпуклой оболочки, целиком расположенных внутри квадрата
с вершинами 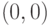 ,
, 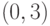 ,
, 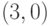 и
и 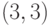 ;
;
g) количество ребер выпуклой оболочке, параллельных осям координат;
h) количество ребер выпуклой оболочке, параллельных сторонам заданного треугольника;
i) угол между максимальным и минимальным ребрами выпуклой оболочки;
j) лежит ли заданная точка плоскости внутри выпуклой оболочки.
Задача 11.11. Модифицируйте текст эталонного проекта "Выпуклая оболочка" так, чтобы индуктивно определить:
a) расстояние от выпуклой оболочки до заданной точки;
b) расстояние от выпуклой оболочки до заданной прямой;
c) расстояние от выпуклой оболочки до заданного отрезка;
d) расстояние от выпуклой оболочки до заданного треугольника;
e) расстояние от выпуклой оболочки до заданного стандартного прямоугольника;
f) среднее арифметическое расстояний от заданной точки до вершин выпуклой оболочки;
g) сумму квадратов расстояний от заданной точки до вершин выпуклой оболочки;
h) сумму квадратов расстояний от начала координат до середин сторон выпуклой оболочки;
i) количество пар вершин выпуклой оболочки, расстояние между которыми не превосходит единицу;
j) количество пар сторон выпуклой оболочки, расстояние между которыми не превосходит единицу.
Задача 11.12. Модифицируйте текст эталонного проекта "Выпуклая оболочка" так, чтобы индуктивно определить:
a) находится ли единичная окружность с центром в начале координат внутри выпуклой оболочки;
b) количество вершин выпуклой оболочки, расположенных в кольце 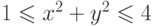 ;
;
c) количество вершин выпуклой оболочки, расстояние от которых до квадрата с
вершинами 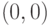 ,
, 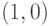 ,
, 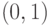 и
и 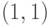 не превосходит единицу;
не превосходит единицу;
d) минимальный стандартный прямоугольник, содержащий выпуклую оболочку (ограничивающий прямоугольник);
e) максимальный стандартный прямоугольник, содержащийся в выпуклой оболочке;
f) радиус минимального круга с центром в заданной точке, содержащего выпуклую оболочку;
g) радиус максимального круга с центром в заданной точке, содержащегося в выпуклой оболочке;
h) диаметр выпуклой оболочки; диаметром 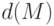 множества
множества  называется точная верхняя граница расстояний между всевозможными точками
множества:
называется точная верхняя граница расстояний между всевозможными точками
множества:
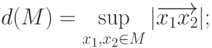
i) длину минимальной диагонали выпуклой оболочки;
j) координаты центра тяжести выпуклой оболочки с вершинами, массы  которых вводятся вместе с их координатами;
которых вводятся вместе с их координатами;  -координата центра тяжести
определяется по формуле
-координата центра тяжести
определяется по формуле
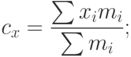
 -координата вычисляется
аналогично.
-координата вычисляется
аналогично.Задача 11.13. Модифицируйте текст эталонного проекта "Выпуклая оболочка" так, чтобы индуктивно определить:
a) мощность множества точек пересечения границы выпуклой оболочки с окружностью 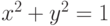 ;
;
b) мощность множества точек пересечения границы выпуклой оболочки с кругом 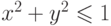 ;
;
c) мощность множества точек пересечения границы выпуклой оболочки с
эллипсом  ;
;
d) мощность множества точек пересечения границы выпуклой оболочки с
гиперболой 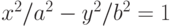 ;
;
e) мощность множества точек пересечения границы выпуклой оболочки с заданной прямой;
f) мощность множества точек пересечения границы выпуклой оболочки с заданным отрезком;
g) мощность множества точек пересечения границы выпуклой оболочки со сторонами заданного стандартного прямоугольника;
h) мощность множества точек пересечения границы выпуклой оболочки с заданным заполненным прямоугольником;
i) мощность множества точек пересечения границы выпуклой оболочки со сторонами заданного треугольника;
j) мощность множества точек пересечения границы выпуклой оболочки с заданным заполненным треугольником.
