|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Сделки без побочных платежей
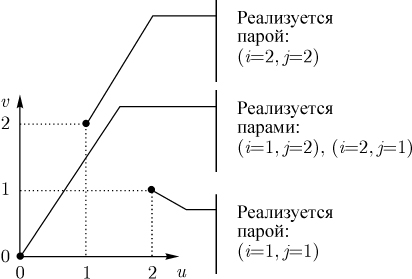
В качестве иллюстрации на рис. 3.1 изображены (темными кружками) точки множества R, соответствующего задаче выбора пункта для строительства с долевым участием, матрицы которой содержатся в табл. 2.8 (см. "Стратегическое равновесие в 2 x 2 играх" ). При этом для каждой точки указаны пары стратегий, совместная реализация которых обеспечивает выигрыши сторон, представленные этой точкой.
Как уже обсуждалось выше, варианты, представленные на рис. 3.1, имеют разную привлекательность для сторон P1 и P2. Поэтому для создания условий кооперации (без побочных платежей) важно расширить множество возможных вариантов. Такое расширение оказывается возможным, например, для повторяющихся сделок, когда соглашения сторон могут относиться не к отдельному акту выбора, а к поведению во всей серии подобных сделок. В этом случае объектом договоренности может быть принятие смешанной стратегии
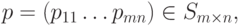 |
( 14.2) |
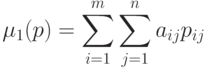 |
( 14.3) |
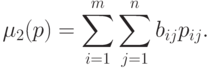 |
( 14.4) |
В качестве иллюстрации вернемся к примеру, представленному на рис. 3.1, и рассмотрим согласованную смешанную стратегию сторон P1 и P2 вида
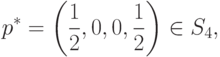 |
( 14.5) |
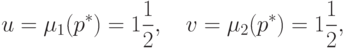
Заметим, что, согласно (14.3)
и (14.4), каждая пара 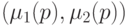 есть выпуклая
линейная комбинация точек множества R из (14.1)
с весами pij,
есть выпуклая
линейная комбинация точек множества R из (14.1)
с весами pij,  ,
, 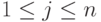 .
Следовательно, множество
.
Следовательно, множество
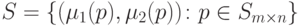 |
( 14.6) |
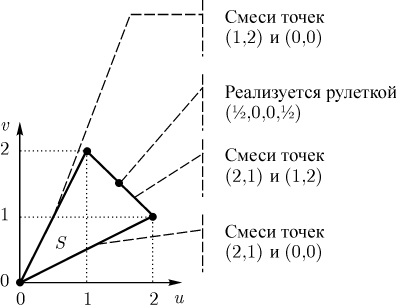
В силу конечности множества R его выпуклая оболочка S представляет собой наименьший плоский многоугольник, включающий все точки из R (см. треугольник, являющийся образом множества S в примере, представленном на рис. 3.2). При этом вершинами такого многоугольника могут быть лишь точки из R (причем не обязательно все точки из R ).
В связи с отмеченной выше реализуемостью любой пары ожидаемых выигрышей (u,v) из множества S (обеспечиваемой согласованным выбором сторонами P1 и P2 соответствующей рулетки) его называют допустимым множеством.