|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Нормальная форма конечной игры. Задание конечной игры в позиционной форме
Матричные и биматричные игры
Определение 2.1 (конечных, матричных и биматричных игр) Игра (1.16) называется конечной, если множества X и Y стратегий сторон P1 и P2 являются конечными. В конечной игре можно занумеровать стратегии сторон целыми числами и рассматривать эти числа как указатели стратегий:
 |
( 8.1) |
 , то их значения
можно представить с помощью таблиц A и B. Строки
этих таблиц
(с номерами
, то их значения
можно представить с помощью таблиц A и B. Строки
этих таблиц
(с номерами  ) соответствуют стратегиям первого игрока,
а столбцы (с номерами
) соответствуют стратегиям первого игрока,
а столбцы (с номерами  ) - стратегиям второго
игрока.
) - стратегиям второго
игрока.Так как пара таблиц A и B полностью описывает модель (1.16) конечной игры (т.е. задает множества X,Y из (8.1) и функции M1(i,j)=aij, M2(i,j)=bij ), то конечная игра двух лиц называется также биматричной игрой.
В случае, когда интересы сторон являются антагонистическими и, согласно (6.2)
 |
( 8.2) |
Пример 2.1 (соглашение об ограничениях при ловле рыбы). Пусть две страны, осуществляющие лов рыбы в одних и тех же водах, согласились на взаимное ограничение добычи с целью сохранения рыбных запасов. При этом каждая из сторон не имеет реальных средств, чтобы контролировать соблюдение соглашения другой стороной. Это обстоятельство исключает возможность применения санкций за нарушения.
Возможные стратегии сторон состоят в том, чтобы соблюдать или не соблюдать принятые соглашения. Доходы сторон (в некоторых условных единицах), соответствующие различным выборам стратегий, представлены парами целых чисел (разделенных запятыми) в следующей таблице. При этом первый коэффициент каждой пары соответствует элементу матрицы A, а второй коэффициент - элементу матрицы B.
| Матрица A и B | Стратегия P2 | ||
| Соблюдать соглашение | Не соблюдать соглашение | ||
| Стратегия P1 | Соблюдать соглашение | 10,10 | 5,11 |
| Не соблюдать соглашение | 11,5 | 6,6 | |
Как следует из определения равновесия по Нэшу, в задаче существует единственная пара стратегий
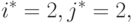 |
( 8.3) |
При этом, например, решение i=j=1, предполагающее взаимное соблюдение соглашения, обеспечивает каждой из сторон больший доход, чем решение (8.3). Однако решение i=j=1 не является устойчивым. Итак, (8.3) есть единственное устойчивое решение в рассматриваемой задаче и оно не эффективно (т.е. улучшаемо). Все остальные решения эффективны (оптимальны по Парето), но не устойчивы.
Определение 2.2 (седлового значения матрицы). В случае
матричных игр определение (6.3) седловой
точки  ядра игры может быть переписано
в виде
ядра игры может быть переписано
в виде
 |
( 8.4) |
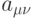 ,
соответствующий значению ядра в седловой точке,
называется седловым значением
матрицы игры. Заметим, что этот коэффициент (если он
существует) является минимальным числом в содержащей его строке и - максимальным
числом в содержащем его столбце.
,
соответствующий значению ядра в седловой точке,
называется седловым значением
матрицы игры. Заметим, что этот коэффициент (если он
существует) является минимальным числом в содержащей его строке и - максимальным
числом в содержащем его столбце.В качестве иллюстрации рассмотрим таблицу, которая соответствует матрице
некоторой игры (описание этой игры будет дано ниже). Как следует из
таблицы и из условий (8.4), пары стратегий  ,
, 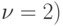 и
и 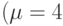 ,
, 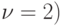 соответствуют седловым точкам ядра и, следовательно, устойчивы по
Нэшу. Заметим, что отвечающие им седловые значения a32 и a42 являются одинаковыми, что согласуется с третьим утверждением следствия из
теоремы об условиях существования седловой точки ядра.
соответствуют седловым точкам ядра и, следовательно, устойчивы по
Нэшу. Заметим, что отвечающие им седловые значения a32 и a42 являются одинаковыми, что согласуется с третьим утверждением следствия из
теоремы об условиях существования седловой точки ядра.
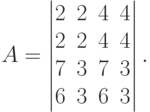
Случай, когда матричная игра не имеет устойчивых решений, иллюстрирует следующий пример, который можно считать классическим.
Пример 2.2 (игра в орлянку). Пусть каждый из игроков независимо выбирает одну из двух сторон монеты, соответственно именуемых "Орел" и "Решка". Если выборы сторон совпали, то игрок P2 отдает монету игроку P1. В противном случае монету получает игрок P2 (за счет игрока P1 ). Если принять номинал монеты за единицу, то этой антагонистической игре соответствует матрица из табл. 2.1.
Матрица этой игры не содержит седловых значений, поскольку максимальные элементы первого и второго столбцов не являются минимальными числами в содержащих их строках. Заметим, что указанное отсутствие устойчивых стратегических пар ведет к недостаточности принципа максимального гарантированного результата для выбора решений. Т.е. этот принцип не может быть удовлетворительной основой для рекомендаций, определяющих поведение.
Согласно (6.18) и (6.19), нижняя и верхняя цены игры в орлянку равны соответственно числам -1 и +1. Сторона P1, соглашаясь на гарантированный уровень полезности, который обеспечивается применением ее максиминной стратегией, получает доход, равный нижней цене игры (т.е. -1 ). При этом она отдает другой стороне величину +1, существенно превышающую тот уровень дохода, который сторона P2 может гарантировать себе сама. Поэтому представляет интерес более полное раскрытие условий, при которых обеспечивается существование устойчивых решений. Необходимо также определение эффективных способов поведения сторон в условиях, когда отсутствуют решения, отвечающие понятию устойчивости, которое было введено в "Устойчивость и эффективность поведения сторон: совместимость свойств устойчивости и эффективности" .

