|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Жадные алгоритмы и матроиды
Взвешенные паросочетания
Рассмотрим следующую задачу. Дан двудольный граф 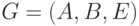 и
для
каждой вершины
и
для
каждой вершины 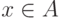 задан положительный
вес
задан положительный
вес 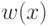 . Требуется
найти такое паросочетание в этом графе, чтобы сумма весов вершин
из доли
. Требуется
найти такое паросочетание в этом графе, чтобы сумма весов вершин
из доли  , инцидентных ребрам паросочетания, была максимальной.
Эту задачу иногда интерпретируют следующим образом.
, инцидентных ребрам паросочетания, была максимальной.
Эту задачу иногда интерпретируют следующим образом.  - это множество работ, а
- это множество работ, а  - множество
работников.
Ребро в графе
- множество
работников.
Ребро в графе  соединяет
вершину
соединяет
вершину 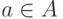 с вершиной
с вершиной 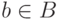 , если
квалификация
работника
, если
квалификация
работника  позволяет ему выполнить работу
позволяет ему выполнить работу  . Каждая
работа
выполняется одним работником. Выполнение работы
. Каждая
работа
выполняется одним работником. Выполнение работы  принесет
прибыль
принесет
прибыль  . Требуется так распределить обязанности работников, чтобы
максимизировать общую прибыль. Покажем, что эта задача может быть решена
алгоритмом СПО в сочетании с методом чередующихся цепей.
. Требуется так распределить обязанности работников, чтобы
максимизировать общую прибыль. Покажем, что эта задача может быть решена
алгоритмом СПО в сочетании с методом чередующихся цепей.
Множество 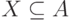 назовем отображаемым, если в графе
назовем отображаемым, если в графе  существует паросочетание
существует паросочетание  , насыщающее все вершины из
, насыщающее все вершины из  .
.  в этом случае будем называть отображением для
в этом случае будем называть отображением для  .
Пусть
.
Пусть  - семейство всех отображаемых множеств.
- семейство всех отображаемых множеств.
Теорема 3. Пара  является матроидом.
является матроидом.
Доказательство. Условие (1) определения матроида, очевидно,
выполняется. Докажем, что выполняется и условие (2).
Пусть 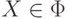 ,
,  ,
, 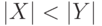 .
Рассмотрим подграф
.
Рассмотрим подграф  графа
графа  , порожденный всеми
вершинами из
, порожденный всеми
вершинами из 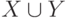 и всеми смежными
с ними вершинами из доли
и всеми смежными
с ними вершинами из доли  .
Пусть
.
Пусть 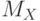 - отображение для
- отображение для  .
Так как
.
Так как 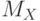 не является наибольшим паросочетанием
в графе
не является наибольшим паросочетанием
в графе  , то по теореме 6 относительно
него в этом графе существует увеличивающая цепь. Одним из концов этой цепи
является свободная относительно
, то по теореме 6 относительно
него в этом графе существует увеличивающая цепь. Одним из концов этой цепи
является свободная относительно 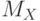 вершина
вершина 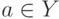 . После
увеличения паросочетания
. После
увеличения паросочетания 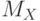 с использованием этой цепи, как
было
описано выше, получим паросочетание
с использованием этой цепи, как
было
описано выше, получим паросочетание 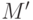 , отображающее множество
, отображающее множество 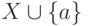 . Следовательно,
. Следовательно, 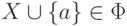 .
.
Даже если бы в задаче требовалось найти только отображаемое множество
наибольшего веса, проверка принадлежности множества семейству  требовала бы и нахождения соответствующего отображения, т.е.
паросочетания. На самом же деле построение паросочетания входит в условие
задачи. Комбинируя СПО с алгоритмом поиска увеличивающих цепей, получаем
следующий алгоритм.
требовала бы и нахождения соответствующего отображения, т.е.
паросочетания. На самом же деле построение паросочетания входит в условие
задачи. Комбинируя СПО с алгоритмом поиска увеличивающих цепей, получаем
следующий алгоритм.
Алгоритм 2. Построение паросочетания наибольшего
веса в двудольном графе 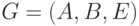 с заданными весами
вершин доли
с заданными весами
вершин доли  .
.
- Упорядочить элементы множества
 по убыванию весов:
по убыванию весов: 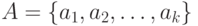 ,
, 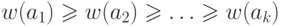
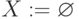
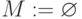
-
for
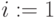 to
to  do
do
-
if в
 существует
увеличивающая
цепь
существует
увеличивающая
цепь  относительно
относительно  ,
начинающаяся в вершине
,
начинающаяся в вершине 
-
then
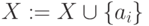 ;
; 
Если для поиска увеличивающей цепи применить метод поиска в ширину, как
описано выше, то время поиска будет пропорционально числу ребер. Общая
трудоемкость алгоритма будет  , где
, где  -
число ребер
в доле
-
число ребер
в доле  .
.
