|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Оптимальные каркасы
Алгоритм Крускала
Другой жадный алгоритм для задачи об оптимальном каркасе известен как алгоритм Крускала.
В нем тоже на каждом шаге
рассматривается частичное решение. Отличие от алгоритма Прима состоит
в том, что в алгоритме Крускала частичное решение всегда представляет собой
остовный лес  графа
графа  , т.е. лес, состоящий из
всех вершин
графа
, т.е. лес, состоящий из
всех вершин
графа  и некоторых его ребер. Вначале
и некоторых его ребер. Вначале  не
содержит ни
одного ребра, т.е. состоит из изолированных вершин. Затем к нему
последовательно добавляются ребра, пока не будет построен каркас
графа
не
содержит ни
одного ребра, т.е. состоит из изолированных вершин. Затем к нему
последовательно добавляются ребра, пока не будет построен каркас
графа  .
Пусть
.
Пусть  - лес, построенный к очередному шагу. Ребро
графа, не принадлежащее
- лес, построенный к очередному шагу. Ребро
графа, не принадлежащее  , назовем красным, если вершины этого
ребра принадлежат одной компоненте связности леса
, назовем красным, если вершины этого
ребра принадлежат одной компоненте связности леса  , и зеленым,
если они принадлежат разным компонентам. Если к
, и зеленым,
если они принадлежат разным компонентам. Если к  добавить
красное
ребро, то образуется цикл. Если же к
добавить
красное
ребро, то образуется цикл. Если же к  добавить зеленое ребро, то
получится новый лес, в котором будет на одну компоненту связности меньше,
чем в
добавить зеленое ребро, то
получится новый лес, в котором будет на одну компоненту связности меньше,
чем в  , так как в результате добавления ребра две компоненты
сольются в одну. Таким образом, к
, так как в результате добавления ребра две компоненты
сольются в одну. Таким образом, к  нельзя добавить никакое
красное ребро и можно добавить любое зеленое. Для выбора добавляемого
ребра применяется тот же "жадный" принцип, что и в алгоритме Прима
-
из всех зеленых ребер выбирается ребро наименьшего веса. Для того чтобы
облегчить поиск этого ребра, вначале все ребра графа упорядочиваются по
возрастанию весов:
нельзя добавить никакое
красное ребро и можно добавить любое зеленое. Для выбора добавляемого
ребра применяется тот же "жадный" принцип, что и в алгоритме Прима
-
из всех зеленых ребер выбирается ребро наименьшего веса. Для того чтобы
облегчить поиск этого ребра, вначале все ребра графа упорядочиваются по
возрастанию весов: 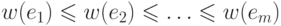 .
Теперь последовательность ребер
.
Теперь последовательность ребер 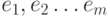 достаточно просмотреть один раз и для очередного рассматриваемого ребра
нужно только уметь определять, является ли оно красным или зеленым
относительно построенного к этому моменту леса
достаточно просмотреть один раз и для очередного рассматриваемого ребра
нужно только уметь определять, является ли оно красным или зеленым
относительно построенного к этому моменту леса  . Красные ребра
просто пропускаются, а зеленые добавляются к
. Красные ребра
просто пропускаются, а зеленые добавляются к  .
.
Для более формального описания алгоритма заметим, что текущий
лес  определяет разбиение множества вершин графа на области связности этого
леса:
определяет разбиение множества вершин графа на области связности этого
леса: 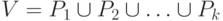 и что красное
ребро - это такое ребро, у которого обе вершины принадлежат одной части
разбиения. Пусть
и что красное
ребро - это такое ребро, у которого обе вершины принадлежат одной части
разбиения. Пусть  - функция, возвращающая для
каждой
вершины
- функция, возвращающая для
каждой
вершины  имя той части разбиения, которой
принадлежит
имя той части разбиения, которой
принадлежит  ,
а
,
а  - процедура, которая по именам
- процедура, которая по именам  и
и  двух
частей разбиения строит новое разбиение, заменяя эти две части их
объединением. Пусть
двух
частей разбиения строит новое разбиение, заменяя эти две части их
объединением. Пусть  ,
, 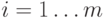 .
Тогда алгоритм Крускала (после упомянутого упорядочения ребер) можно
записать следующим образом.
.
Тогда алгоритм Крускала (после упомянутого упорядочения ребер) можно
записать следующим образом.
Алгоритм 2. Построение оптимального каркаса методом Крускала
-
for
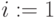 to
to  do
do
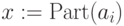
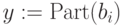
-
if
 then
then 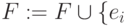 ,
, 
Более подробно алгоритм Крускала рассматривается во второй части (в разделе, посвященном разделенным множествам). Корректность этого алгоритма следует из общей теоремы Радо-Эдмондса, которая будет рассмотрена в "следующей лекции" .
