|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Инспектор
Вы можете этот курс.
Опубликован: 27.09.2006 | Уровень: специалист | Доступ: платный | ВУЗ: Нижегородский государственный университет им. Н.И.Лобачевского
Лекция 11:
Рационализация переборных алгоритмов
Хордальные графы
Граф называется хордальным
(или триангулированным ), если в нем
нет порожденных простых циклов длины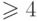 
. Иначе говоря,
в хордальном графе для каждого простого цикла длины 4 или больше имеется
хотя бы одна хорда - ребро, не принадлежащее циклу, но соединяющее две
вершины цикла.
Теорема 2. В любом непустом хордальном графе имеется смежно поглощающая вершина.
Доказательство. Пусть 
- непустой граф, в котором нет
смежно поглощающих вершин. Докажем, что - не хордальный.
Рассмотрим в нем простой путь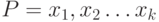 
наибольшей длины, не имеющий хорд, то есть ребер, соединяющих две вершины
пути и не принадлежащих пути. Так как граф непустой, то 
.
Рассмотрим вершину 
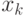. Так как она не поглощает вершину 
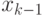, то существует вершина 
,
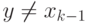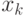смежная с вершиной , но не смежная с 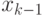. Вершина 
не
принадлежит пути 
, так как иначе ребро 
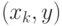было бы
хордой этого пути. Таким образом, последовательность 
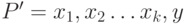является простым путем. Но длина этого пути больше,
чем длина пути , поэтому, в силу выбора пути ,
у пути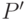 
должна существовать хорда. Такой хордой может быть
только ребро
вида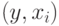 
, где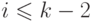 
. Пусть 
-
наибольшее, при котором ребро 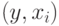является хордой
пути .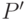
Тогда последовательность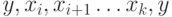 
является циклом без хорд длины не менее 4.
Итак, для хордального графа наибольшее независимое множество можно найти с помощью одних только сжатий по включению. Нужно только находить смежно поглощающие вершины и удалять их из графа до тех пор, пока оставшийся граф не станет пустым. Множество оставшихся вершин и является наибольшим независимым множеством.
Рационализация алгоритма для задачи о раскраске вершин
В описанную схему решения задачи о раскраске можно включить тот же прием
сжатия по включению, что и для задачи о независимом множестве. Небольшое
отличие состоит в том, что теперь вершины 
и 
должны
быть несмежны. Итак, пусть в графе имеются две
несмежные вершины и , такие,
что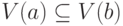 
.
Будем говорить, что вершина несмежно
поглощает вершину , а вершину называть несмежно
поглощаемой. В графе на рис. 11.1
вершина 1
несмежно поглощает вершину 4, а вершина 3 - вершину 7.
Теорема 3. Если вершина является несмежно
поглощаемой в графе , то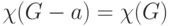 
.
Доказательство. Допустим, вершина несмежно поглощается вершиной .
Рассмотрим правильную раскраску графа 
в наименьшее число
цветов.
Применим эту же раскраску к графу , окрасим вершину
в тот цвет, который имеет вершина . Так как вершина
смежна только с такими вершинами, с которыми смежна ,
то получится правильная раскраска графа в то же самое число
цветов. Следовательно,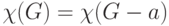 
.
Как и для задачи о независимом множестве, для некоторых графов этот прием
позволяет находить решение, совсем не прибегая к перебору. Допустим,
вершина смежно поглощает вершину
в графе .
Тогда в дополнительном графе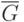 
, очевидно,
вершина
будет несмежно поглощать вершину . Верно и обратное утверждение.
Поэтому из теоремы 2 следует
Теорема 4. В любом графе, дополнительном к хордальному и не являющемся полным, имеется несмежно поглощаемая вершина.
Таким образом, для графов, дополнительных к хордальным, раскраска в минимальное число цветов может быть найдена с помощью одних только сжатий по включению. Оказывается, и для хордальных графов существует эффективное решение задачи о раскраске.
Установим сначала некоторые свойства хордальных графов. Подмножество множества вершин графа называется разделяющим множеством, если удаление всех этих вершин приводит к увеличению числа компонент связности. Таким образом, понятие разделяющего множества является обобщением понятия шарнира. Разделяющее множество называется минимальным, если оно не содержится в большем разделяющем множестве.
Татьяна Наумович
