Эйлеровы и гамильтоновы циклы

Гамильтоновы пути и циклы

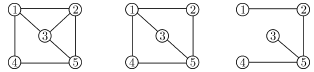
Гамильтоновым циклом ( путем ) называют простой цикл (путь), содержащий все вершины графа. В графе, изображенном на рис. 8.1 слева, гамильтоновым циклом является, например, последовательность , , , , , 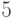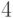. В графе, изображенном в центре, нет гамильтоновых циклов, но есть гамильтоновы пути, например, . В правом графе нет и гамильтоновых путей.

Рис. 8.1.

Внешне определение гамильтонова цикла похоже на определение эйлерова цикла. Однако есть кардинальное различие в сложности решения соответствующих задач распознавания и построения. Мы видели, что имеется достаточно простой критерий существования эйлерова цикла и эффективный алгоритм его построения. Для гамильтоновых же циклов (и путей) неизвестно никаких просто проверяемых необходимых и достаточных условий их существования, а все известные алгоритмы требуют для некоторых графов перебора большого числа вариантов.

Гамильтонов цикл представляет собой, с комбинаторной точки зрения, просто перестановку вершин графа. При этом в качестве начальной вершины цикла можно выбрать любую вершину, так что можно рассматривать перестановки с фиксированным первым элементом. Самый бесхитростный план поиска гамильтонова цикла состоит в последовательном рассмотрении всех этих перестановок и проверке для каждой из них, представляет ли она цикл в данном графе. Такой способ действий уже при не очень большом числе вершин становится практически неосуществимым ввиду быстрого роста числа перестановок - имеется 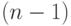! перестановок из элементов с фиксированным первым элементом.

Более рациональный подход состоит в рассмотрении всевозможных простых путей, начинающихся в произвольно выбранной стартовой вершине , до тех пор, пока не будет обнаружен гамильтонов цикл или все возможные пути не будут исследованы. По сути дела, речь тоже идет о переборе перестановок, но значительно сокращенном - если, например, вершина не смежна с вершиной , то все 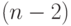! перестановок, у которых на первом месте стоит , а на втором , не рассматриваются.

Рассмотрим этот алгоритм подробнее. Будем считать, что граф задан окрестностями вершин: для каждой вершины задано множество вершин, смежных с . На каждом шаге алгоритма имеется уже построенный отрезок пути, он хранится в стеке PATH. Для каждой вершины , входящей в PATH, хранится множество всех вершин, смежных с , которые еще не рассматривались в качестве возможных продолжений пути из вершины . Когда вершина добавляется к пути, множество полагается равным 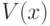. В дальнейшем рассмотренные вершины удаляются из этого множества. Очередной шаг состоит в исследовании окрестности последней вершины пути PATH. Если и в имеются вершины, не принадлежащие пути, то одна из таких вершин добавляется к пути. В противном случае вершина исключается из стека. Когда после добавления к пути очередной вершины оказывается, что путь содержит все вершины графа, остается проверить, смежны ли первая и последняя вершины пути, и при утвердительном ответе выдать очередной гамильтонов цикл.

Алгоритм 2. Поиск гамильтоновых циклов

1. выбрать произвольно вершину
2. 
3. 
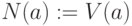
4. while do
5. 
6. if
7. then взять
8. 
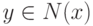
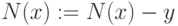
9. if вершина не находится в PATH
10. then
11. 
12. if PATH содержит все вершины
13. then if смежна с
14. then выдать цикл
15. else удалить вершину из PATH

Этот алгоритм очень похож на алгоритм поиска в глубину и отличается от него по существу только тем, что открытая вершина, когда вся ее окрестность исследована, не закрывается, а опять становится новой (исключается из стека). В начале все вершины новые. Процесс заканчивается, когда все вершины опять станут новыми. На самом деле это и есть поиск в глубину, только не в самом графе, а в дереве путей. 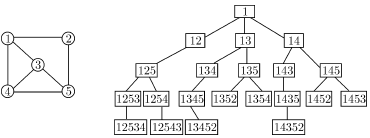Вершинами этого дерева являются всевозможные простые пути, начинающиеся в вершине , а ребро дерева соединяет два пути, один из которых получается из другого добавлением одной вершины в конце. На рис. 8.2 показаны граф и его дерево путей из вершины .

Рис. 8.2.