|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Пространство циклов графа
Фундаментальные циклы
Компактное представление пространства дает его базис. Если выписать все
простые циклы графа  , то это в большинстве случаев не будет его
базисом, так как некоторые из этих циклов могут быть суммами других
(см. пример на рис. 7.1). Построить базис пространства
, то это в большинстве случаев не будет его
базисом, так как некоторые из этих циклов могут быть суммами других
(см. пример на рис. 7.1). Построить базис пространства ![C[G]](/sites/default/files/tex_cache/40f7582c1aef765b7b3649cd37f50564.png) , состоящий из простых циклов, можно следующим образом. Выберем в графе
, состоящий из простых циклов, можно следующим образом. Выберем в графе  какой-нибудь каркас
какой-нибудь каркас  . Пусть
. Пусть 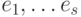 - все ребра
графа
- все ребра
графа  , не принадлежащие
, не принадлежащие  . Если добавить к
. Если добавить к  ребро
ребро 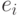 , то в полученном графе образуется единственный
(простой)
цикл
, то в полученном графе образуется единственный
(простой)
цикл  . Таким образом, получаем семейство из
. Таким образом, получаем семейство из  циклов,
они называются фундаментальными циклами относительно
каркаса
циклов,
они называются фундаментальными циклами относительно
каркаса  .
.
Теорема 2. Множество всех фундаментальных циклов относительно
любого каркаса  графа
графа  образует базис
пространства циклов этого графа.
образует базис
пространства циклов этого графа.
Доказательство. Зафиксируем некоторый каркас  и рассмотрим
фундаментальные циклы
и рассмотрим
фундаментальные циклы  относительно
этого
каркаса. В каждом из этих циклов имеется ребро
относительно
этого
каркаса. В каждом из этих циклов имеется ребро 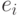 ,
принадлежащее
данному циклу и не принадлежащее никакому из остальных. Поэтому при
сложении этого цикла с другими фундаментальными циклами данное
ребро не "уничтожится" - оно будет присутствовать в
суммарном графе.
Следовательно, сумма различных фундаментальных циклов никогда не будет
пустым графом, то есть фундаментальные циклы линейно независимы.
,
принадлежащее
данному циклу и не принадлежащее никакому из остальных. Поэтому при
сложении этого цикла с другими фундаментальными циклами данное
ребро не "уничтожится" - оно будет присутствовать в
суммарном графе.
Следовательно, сумма различных фундаментальных циклов никогда не будет
пустым графом, то есть фундаментальные циклы линейно независимы.
Покажем теперь, что любой квазицикл графа  является суммой
фундаментальных циклов. Действительно, пусть
является суммой
фундаментальных циклов. Действительно, пусть  - такой
квазицикл.
Пусть
- такой
квазицикл.
Пусть 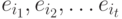 - все
ребра
- все
ребра  ,
не принадлежащие
,
не принадлежащие  . Рассмотрим граф
. Рассмотрим граф 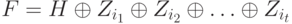 . Каждое из ребер
. Каждое из ребер 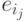 ,
, 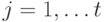 , входит ровно в два
слагаемых этой
суммы - в
, входит ровно в два
слагаемых этой
суммы - в  и в
и в 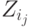 . Следовательно,
при сложении все
эти ребра уничтожатся. Все остальные ребра, присутствующие
в графах-слагаемых, принадлежат
. Следовательно,
при сложении все
эти ребра уничтожатся. Все остальные ребра, присутствующие
в графах-слагаемых, принадлежат  . Значит,
. Значит,  - подграф
графа
- подграф
графа  . Так как все слагаемые являются квазициклами,
значит,
. Так как все слагаемые являются квазициклами,
значит,  -
тоже квазицикл. Но в
-
тоже квазицикл. Но в  нет циклов, поэтому имеется
единственная возможность:
нет циклов, поэтому имеется
единственная возможность:  , откуда получаем
, откуда получаем  .
.
Из этой теоремы следует, что размерность пространства циклов графа равна
числу ребер, не входящих в его каркас. Так как каркас содержит 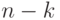 ребер, где
ребер, где  - число компонент связности графа, то эта
размерность
равна
- число компонент связности графа, то эта
размерность
равна  . Это число называют цикломатическим числом
графа.
. Это число называют цикломатическим числом
графа.
Построение базы циклов
Базис пространства циклов графа коротко называют базой циклов. На основании теоремы 2 можно предложить достаточно простой способ построения базы циклов графа. Сначала находится какой-нибудь каркас, затем для каждого ребра, не принадлежащего каркасу, отыскивается тот единственный цикл, который это ребро образует с ребрами каркаса. Таким образом, любой алгоритм построения каркаса может быть использован для нахождения базы циклов.
Поиск в глубину особенно удобен благодаря основному свойству DFS-дерева
(теорема 1 из
"Поиск в глубину"
) - каждое обратное ребро относительно этого дерева
является продольным. Это означает, что из двух вершин такого ребра одна
является предком другой в DFS-дереве. Каждое такое ребро в процессе поиска
в глубину встретится дважды - один раз, когда активной вершиной будет
предок, другой раз, когда ею будет потомок. В этом последнем случае
искомый фундаментальный цикл состоит из рассматриваемого обратного ребра
и участка пути в DFS-дереве, соединяющего эти две вершины. Но этот путь так
или иначе запоминается в процессе обхода в глубину, так как он необходим
для последующего возвращения. Если, например, для хранения открытых вершин
используется стек, то вершины этого пути находятся в верхней части стека.
В любом случае этот путь легко доступен и цикл находится без труда.
Запишем процедуру построения фундаментальных циклов на базе алгоритма
поиска в глубину с построением DFS-дерева. Переменная  -
счетчик
циклов,
-
счетчик
циклов, 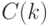 - последовательность (список) вершин,
составляющих цикл
с номером
- последовательность (список) вершин,
составляющих цикл
с номером  .
.
Алгоритм 1. Построение базы циклов.
- пометить все вершины как новые
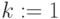
-
for
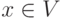 do if
do if  новая then
новая then 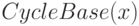
Procedure 
- открыть вершину

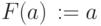
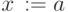
-
while
 открытая do
открытая do
-
if имеется неисследованное
ребро
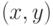
-
then пометить ребро
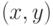 как исследованное
как исследованное -
if вершина
 новая
новая -
then открыть
вершину

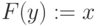

-
else
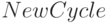
-
else закрыть вершину

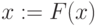
Procedure 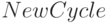
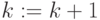
- Создать список
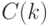 из одного элемента
из одного элемента 

-
repeat

- добавить
 к списку
к списку 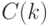
-
until
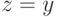
Хотя сам поиск в глубину выполняется за линейное от числа вершин и ребер
время, решающее влияние на трудоемкость этого алгоритма оказывает
необходимость запоминать встречающиеся циклы. Подсчитаем суммарную длину
этих циклов для полного графа с  вершинами. DFS-дерево в этом
случае является простым путем, относительно него будет
вершинами. DFS-дерево в этом
случае является простым путем, относительно него будет 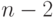 цикла
длины
цикла
длины  ,
, 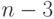 цикла длины
цикла длины 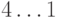 цикл
длины
цикл
длины  . Сумма
длин всех фундаментальных циклов будет равна
. Сумма
длин всех фундаментальных циклов будет равна
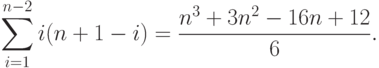
Таким образом, на некоторых графах число операций этого алгоритма будет
величиной порядка 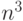 .
.
