НОУ ИНТУИТ | Введение в математическое программирование. Лекция 1: Математическое моделирование. Математическая модель в задачах оптимизации. Элементарные математические модели

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.07.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Донецкий национальный технический университет

|

Вам нравится? Нравится 52 студентам

| Поделиться |

Поддержать программу

3. Применение аналогий при построении моделей. В огромном числе случаев при попытке построить модель какого-либо объекта либо невозможно прямо указать фундаментальные законы или вариационные принципы, которым он подчиняется, либо, с точки зрения наших сегодняшних знаний, вообще нет уверенности в существовании подобных законов, допускающих математическую формулировку. Одним из плодотворных подходов к такого рода объектам является использование аналогий с уже изученными явлениями. Что, казалось бы, общего между радиоактивным распадом и динамикой популяций, в частности изменением численности населения нашей планеты? Однако на простейшем уровне такая аналогия вполне просматривается, о чем свидетельствует одна из простейших моделей популяций, называемая моделью Мальтуса. В ее основу положено простое утверждение - скорость изменения населения со временем t пропорциональна его текущей численности N(t), умноженной на сумму коэффициентов рождаемости 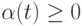$\alpha (t) \geq 0$ и смертности 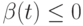$\beta (t) \leq 0$ . В результате приходим к уравнению

$\frac{dN(t)}{dt}=[\alpha(t) - \beta(t)]N(t),$

( 10)

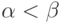весьма похожему на уравнение радиоактивного распада и совпадающего с ним при $\alpha < \beta$ (если $\alpha$ и $\beta$ постоянные). Это неудивительно, так как при их выводе использовались одинаковые соображения. Интегрирование уравнения (10) дает

$N(t)=N(0) \exp \left( \int\limits_{t_0}^t [\alpha(t)-\beta(t)]dt \right),$

где N(0) = N(t = t₀) — начальная численность.

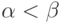На рис. 1.7 приведены графики функции N(t) при постоянных $\alpha$ и $\beta$ (разным подобным друг другу кривым соответствуют разные t₀ — значения времени начала процесса). При $\alpha = \beta$ численность остается постоянной, т.е. в этом случае решением уравнения является равновесная величина N(t) = N(0). 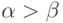Равновесие между рождаемостью и смертностью неустойчиво в том смысле, что даже небольшое нарушение равенства $\alpha = \beta$ приводит с течением времени ко все большему отклонению функции N(t) от равновесного значения N(0). При $\alpha < \beta$ численность населения убывает и стремится к нулю при $t \rightarrow \infty$ , а при $\alpha > \beta$ растет по некоторому экспоненциальному закону, обращаясь в бесконечность при $t \rightarrow \infty$ . Последнее обстоятельство и послужило основанием для опасений Мальтуса о грядущем перенаселении Земли со всеми вытекающими отсюда последствиями.

Рис. 1.7. Изменение численности популяции со временем в модели Мальтуса

Как в данном примере, так и в ряде рассмотренных выше случаев можно указать немало очевидных ограничений применимости построенной модели. Конечно же, сложнейший процесс изменения численности населения, зависящий к тому же от сознательного вмешательства самих людей, не может описываться какими-либо простыми закономерностями. Даже в идеальном случае изолированной биологической популяции предложенная модель не отвечает реальности в полной мере хотя бы из-за ограниченности ресурсов, необходимых для ее существования.

Сделанное замечание тем не менее нисколько не умаляет роли аналогий в построении математических моделей очень сложных явлений.

Применение аналогий основано на одном из важнейших свойств моделей - их универсальности, т. е. их приложимости к объектам принципиально различной природы. Так, предположения типа "скорость изменения величины пропорциональна значению самой величины (или некоторой функции от нее)" широко используются в далеких друг от друга областях знаний.

4. Иерархический подход к получению моделей. Лишь в редких случаях бывает удобным и оправданным построение математических моделей даже относительно простых объектов сразу во всей полноте, с учетом всех факторов, существенных для его поведения. Поэтому естествен подход, реализующий принцип "от простого — к сложному", когда следующий шаг делается после достаточно подробного изучения не очень сложной модели. При этом возникает цепочка ( иерархия ) все более полных моделей, каждая из которых обобщает предыдущие, включая их в качестве частного случая.

Построим такую иерархическую цепочку на примере модели многоступенчатой ракеты. Как было установлено в конце п.1, реальная одноступенчатая ракета неспособна развить первую космическую скорость. Причина этого - затраты горючего на разгон ненужной, отработавшей части структурной массы. Следовательно, при движении ракеты необходимо периодически избавляться от балласта. В практической конструкции это означает, что ракета состоит из нескольких ступеней, отбрасываемых по мере их использования.

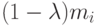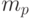Пусть m_i — общая масса i -й ступени, $\lambda m_i$ - соответствующая структурная масса (при этом масса топлива равна величине $(1 - \lambda)m_i$ ), m_p - масса полезной нагрузки. Величины $\lambda$ и скорость истечения газов одинаковы для всех ступеней. Возьмем для определенности число ступеней n = 3. Начальная масса такой ракеты равна

m₀=m_p+m₁+m₂+m₃

Рассмотрим момент, когда израсходовано все топливо первой ступени и масса ракеты равна величине

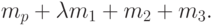
$m_p + \lambda m_1 + m_2 + m_3.$

Тогда по формуле (6) первоначальной модели скорость ракеты равна

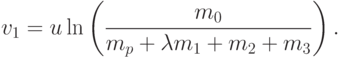
$v_1=u \ln \left( \frac{m_0}{m_p + \lambda m_1 + m_2 + m_3} \right).$

После достижения скорости v₁ структурная масса $\lambda m_1$ отбрасывается и включается вторая ступень. Масса ракеты в этот момент равна

m_p+m₂+m₃

Начиная с этого момента и до момента полного выгорания топлива второй ступени, ничто не мешает пользоваться уже построенной моделью, применив ее к рассматриваемому случаю. Все рассуждения о сохранении суммарного импульса и соответствующие выкладки остаются в силе (следует только учесть, что у ракеты уже есть начальная скорость v_i ). Тогда по формуле (6) после выгорания топлива во второй ступени ракета достигает скорости

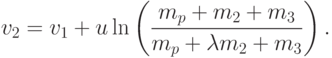
$v_2 = v_1 + u \ln \left( \frac{m_p + m_2 + m_3}{m_p + \lambda m_2 + m_3} \right).$

Такие же рассуждения применимы и к третьей ступени ракеты. После отключения ее двигателей скорость ракеты равна

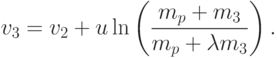
$v_3 = v_2 + u \ln \left( \frac{m_p + m_3}{m_p + \lambda m_3} \right).$

Эту цепочку нетрудно продолжить для любого числа ступеней и получить соответствующие формулы. В случае же n = 3 для окончательной скорости имеем

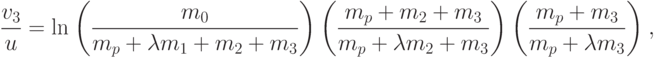
$\frac{v_3}{u} = \ln \left{ \left( \frac{m_0}{m_p + \lambda m_1 + m_2 + m_3} \right) \left( \frac{m_p + m_2 + m_3}{m_p + \lambda m_2 + m_3} \right) \left( \frac{m_p + m_3}{m_p + \lambda m_3} \right) \right},$

или, вводя величины

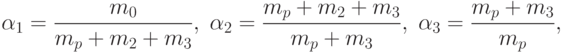
$\alpha_1 = \frac{m_0}{m_p + m_2 + m_3}, \; \alpha_2 = \frac{m_p + m_2 + m_3}{m_p + m_3}, \; \alpha_3 = \frac{m_p + m_3}{m_p},$

Получаем

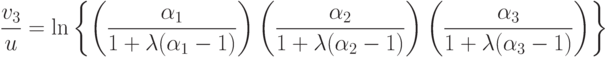
$\frac{v_3}{u} = \ln \left\{ \left( \frac{\alpha_1}{1+\lambda(\alpha_1 - 1)} \right) \left( \frac{\alpha_2}{1+\lambda(\alpha_2 - 1)} \right) \left( \frac{\alpha_3}{1+\lambda(\alpha_3 - 1)} \right) \right\}$

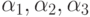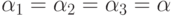Данное выражение симметрично по отношению к величинам $\alpha_1, \alpha_2, \alpha_3$ и нетрудно показать, что его максимум достигается в симметричном случае, т.е. при $\alpha_1 = \alpha_2 = \alpha_3 = \alpha$ . При этом для i = 3

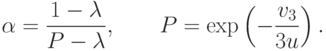
$\alpha = \frac{1 - \lambda}{P - \lambda}, \qquad P = \exp \left( - \frac{v_3}{3u} \right).$

Произведение 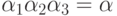$\alpha_1 \alpha_2 \alpha_3 = \alpha$ , как легко проверить, отношению m₀/m_p, или

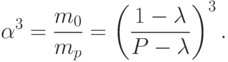
$\alpha^3 = \frac{m_0}{m_p} = \left( \frac{1-\lambda}{P-\lambda} \right)^3.$

Для многоступенчатой ракеты, аналогично, имеем

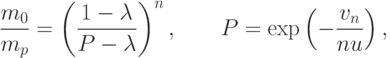$\frac{m_0}{m_p} = \left( \frac{1-\lambda}{P-\lambda} \right)^n, \qquad P= \exp \left( - \frac{v_n}{nu} \right),$

( 11)

где n — число ступеней.

Проанализируем формулу (11). Примем v_n = 10,5 км/с, 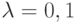$\lambda = 0,1$ . Тогда для n = 2, 3, 4 получаем m₀ = 149 m_р, m₀ = 77 m_p, m₀ = 65 m_p соответственно. Это значит, что двухступенчатая ракета пригодна для выведения на орбиту некоторой полезной массы (однако при одной тонне полезного груза необходимо иметь ракету весом 149 тонн). Переход к третьей ступени уменьшает массу ракеты почти в два раза (но, конечно же, усложняет ее конструкцию), а четырехступенчатая ракета не дает заметного выигрыша по сравнению с трехступенчатой.

Построение иерархической цепочки позволило относительно просто прийти к этим важным выводам. Иерархия математических моделей часто строится и по противоположному принципу "от сложного к простому". В этом случае реализуется путь "сверху вниз" - из достаточно общей и сложной модели при соответствующих упрощающих предположениях получается последовательность все более простых (но имеющих уменьшающуюся область применимости) моделей.

Дальше >>

Введение в математическое программирование

Введение в математическое программирование

Математическое моделирование. Математическая модель в задачах оптимизации. Элементарные математические модели

Вопросы и ответы

Студенты

Авторизоваться

Введение в математическое программирование

Введение в математическое программирование

Математическое моделирование. Математическая модель в задачах оптимизации. Элементарные математические модели

Вопросы и ответы

Студенты