Введение в математическое программирование

:

Введение в математическое программирование
[+]
Опубликован: 09.07.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Донецкий национальный технический университет

Лекция 11: Метод наискорейшего спуска. Метод Давидона – Флетчера – Пауэлла. Проблема оврагов. Проблема многоэкстремальности

A
|
версия для печати
< Лекция 10 || Лекция 11: 123 || Лекция 12 >
Аннотация: В данной лекции широко освещены такие методы многопараметрической оптимизации как метод наискорейшего спуска и метод Давидона – Флетчера – Пауэлла. Кроме того, проводится сравнительный анализ вышеперечисленных методов с целью определения наиболее действенного, выявляются их преимущества и недостатки; а также рассматриваются проблемы многомерной оптимизации, такие как метод оврагов и метод многоэкстремальности.
Ключевые слова: метод покоординатного спуска, направление градиента, наибольшее локальное возрастание, метод наискорейшего спуска, симметрическая матрица, собственный вектор, метод градиентного спуска, градиентного спуска, градиент функции, локальные минимумы

1. Метод наискорейшего спуска

Суть данного метода заключается в том, что с помощью упомянутого ранее метода покоординатного спуска осуществляется поиск из заданной точки в направлении, параллельном одной из осей, до точки минимума в данном направлении. Затем поиск производится в направлении, параллельном другой оси, и т.д. Направления, конечно, фиксированы. Кажется разумным попытаться модифицировать этот метод таким образом, чтобы на каждом этапе поиск точки минимума производился вдоль "наилучшего" направления. Не ясно, какое направление является "наилучшим", но известно, что направление градиента является направлением наискорейшего возрастания функции. Следовательно, противоположное направление является направлением наискорейшего убывания функции. Это свойство может быть обосновано следующим образом.

Предположим, что осуществляется перемещение из точки x в следующую точку х + hd, где d - некоторое направление, a h - шаг некоторой длины. Следовательно, перемещение производится из точки (x1, х2, ..., хn) в точку (x1 + zx1, x2 + zх2, ..., хn + zхn), где

zx_i = hd_i ( 1.1)
a dj - косинусы направления d, такие, что
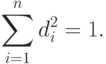\sum_{i=1}^n d_i^2 = 1. ( 1.2)

Изменение значений функции определяется соотношениями

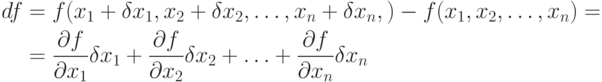\begin{aligned} df & = f(x_1 + \delta x_1, x_2 + \delta x_2, \ldots, x_n + \delta x_n,) - f(x_1, x_2, \ldots, x_n) = \\ & = \frac{\partial f}{\partial x_1} \delta x_1 + \frac{\partial f}{\partial x_2} \delta x_2 + \ldots + \frac{\partial f}{\partial x_n} \delta x_n \end{aligned} ( 1.3)
с точностью до первого порядка zxi, причем частные производные вычисляются в точке x. Как следует выбрать направления di, удовлетворяющие уравнению (1.2), чтобы получить наибольшее значение изменения функции df? Здесь возникает задача максимизации с ограничением. Применим метод множителей Лагранжа, с помощью которого определим функцию
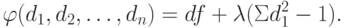
\varphi(d_1,d_2,\ldots,d_n)=df+\lambda(\Sigma d_1^2 -1).

Величина df, удовлетворяющая ограничению (1.2), достигает максимума, когда функция

\varphi(d_1,d_2,\ldots,d_n) = h \left( \frac{\partial f}{\partial x_1}d_1 + \frac{\partial f}{\partial x_2}d_2 + \ldots + \frac{\partial f}{\partial x_n}d_n \right) + \lambda(d_1^2 + d_2^2 + \ldots + d_n^2-1)
достигает максимума. Ее производная
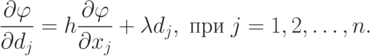
\frac{\partial \varphi}{\partial d_j} = h \frac{\partial \varphi}{\partial x_j} + \lambda d_j, \; \text{при} \; j=1,2,\ldots,n.
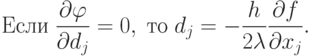\text{Если} \; \frac{\partial \varphi}{\partial d_j} = 0, \; \tetx{то} \; d_j = - \frac{h}{2\lambda} \frac{\partial f}{\partial x_j} . ( 1.5)

Следовательно,

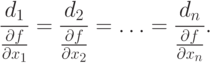\frac{d_1}{\frac{\partial f}{\partial x_1}} = \frac{d_2}{\frac{\partial f}{\partial x_2}} = \ldots = \frac{d_n}{\frac{\partial f}{\partial x_n}} . ( 1.6)

Тогда di ~ df/dxi и направление d параллельно направлению V/(x) в точке х.

Таким образом, наибольшее локальное возрастание функции для заданного малого шага h имеет место, когда d есть направление Vf(x) или g(х). Поэтому направлением наискорейшего спуска является направление

-\nabla f(x) \;\; \text{или} \; -g(x). ( 1.7)

В более простом виде уравнение (1.3) можно записать так:

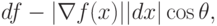
df-|\nabla f(x)||dx|\cos \theta ,
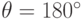где \theta - угол между векторами Vf(x) и dx. Для заданной величины dx мы минимизируем df, выбирая \theta = 180^{\circ}, чтобы направление dx совпадало с направлением -Vf(x).

Замечание. Направление градиента перпендикулярно в любой точке линии постоянного уровня, поскольку вдоль этой линии функция постоянна. Таким образом, если (d1, d2, ..., dn) - малый шаг вдоль линии уровня, то

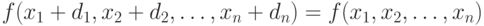
f(x_1 + d_1, x_2 + d_2, \ldots, x_n + d_n)=f(x_1, x_2, \ldots, x_n)
и, следовательно,
df = \sum_{j=1}^n \frac{\partial f}{\partial x_j} \, d_j = [\nabla f(x)]^T d =0. ( 1.8)
(рис. 11.1)


Рис. 11.1.

В методе наискорейшего спуска желательно использовать рассмотренное свойство направления градиента. Поэтому, если мы находимся в точке xi на некотором шаге процесса оптимизации, то поиск минимума функции осуществляется вдоль направления -Vf(xj). Данный метод является итерационным. На шаге i точка минимума аппроксимируется точкой xi. Следующей аппроксимацией является точка

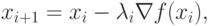x_{i+1} = x_i - \lambda_i \nabla f(x_i), ( 1.9)
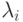где \lambda_i - значение \lambda, минимизирующее функцию
\varphi(\lambda) = f[x_i - \lambda \nabla f(x_i)]. ( 1.10)

Значение 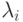\lambda_i может быть найдено с помощью одного из методов одномерного поиска. Блок-схема метода наискорейшего спуска приведена на рис. 11.2.


Рис. 11.2.
Дальше >>
< Лекция 10 || Лекция 11: 123 || Лекция 12 >

Вопросы и ответы

вопросов: 0

Студенты

всего: 56
Дмитрий Сушанский
Дмитрий Сушанский
Россия
предложить дружбу
Евгения Емельянова
Евгения Емельянова
Россия
предложить дружбу