НОУ ИНТУИТ | Введение в математическое программирование. Лекция 11: Метод наискорейшего спуска. Метод Давидона – Флетчера – Пауэлла. Проблема оврагов. Проблема многоэкстремальности

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.07.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Донецкий национальный технический университет

|

Вам нравится? Нравится 52 студентам

| Поделиться |

Поддержать программу

2. Метод Давидона - Флетчера – Пауэлла

Начнем поиск из начальной точки x₀, взяв в качестве начальной матрицу Н0 (обычно единичную матрицу, хотя в этом случае может подойти любая симметрическая положительно определенная матрица). Итерационная процедура может быть представлена следующим образом.

На шаге i имеются точка x_i и положительно определенная симметрическая матрица H_i.
В качестве направления поиска взять направление
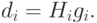
( 2.1)
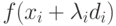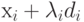Чтобы найти функцию x_i, минимизирующую функцию $f(x_i + \lambda_i d_i)$ , произвести одномерный поиск вдоль прямой $х_i + \lambda_i d_i$ .
Положить
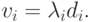
$v_i = \lambda_i d_i .$ ( 2.2)
Положить
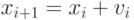
$x_{i+1} = x_i + v_i$ ( 2.3)
Найти f(x_i+1) и g_i+1. Завершить процедуру, если величины |g_i+1| или |V_i| достаточно малы. В противном случае продолжить.
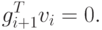
$g_{i+1}^T v_i = 0.$
Положить
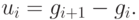
$u_i = g_{i+1} - g_i.$ ( 2.5)
Обновить матрицу H следующим образом:
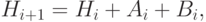
$H_{i+1} = H_i + A_i +B_i,$ ( 2.6)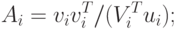
где
( 2.7)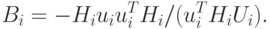
Увеличить i на единицу и вернуться на шаг 2.

Поясним процедуру, следуя аргументации Флетчера и Пауэлла.

а) Процесс будет устойчив, если функция v_i убывает и величина 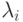$\lambda_i$ положительна. Поскольку g_i есть направление наискорейшего возрастания, функция v_i будет убывать тогда, когда произведение

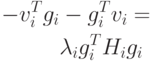$\begin{aligned} -v_i^T g_i & -g_i^T v_i = \\ & \lambda_i g_i^T H_i g_i \end{aligned}$

( 2.9)

положительно.

Это справедливо, если H_i - симметрическая положительно определенная матрица для любого i. Начальная матрица Н₀ обладает этими свойствами по определению. Процесс обновления в соответствии с соотношениями 2.6 – 2.8 сохраняет симметричность гессиана. Методом индукции докажем, что после обновления матрица H_i остается положительно определенной. Если это условие справедливо, то

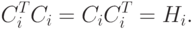( 2.10)

Положим

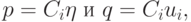$p = C_i \eta \; \text{и } q = C_i u_i ,$

( 2.11)

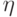где $\eta$ - произвольный вектор.

Тогда

$\begin{aligned} \eta^T H_{i+1} \eta & \eta^T H_i \eta + \frac{\eta^T v_i v_i^T \eta}{v_i^T u_i} - \frac{\eta^T H_i u_i u_i^T H_i \eta}{u_i^T H_i u_i} = \\ & p^2 - \frac{(p^T q)^2}{q^2} + \frac{(\eta^T v_i)^2}{v_i^T u_i} = \\ & \frac{p^2 q^2 - (p^T q)^2}{q^2} + \frac{(\eta^T v_i)^2}{v_i^T u_i} \geqslant \\ & \geqslant \frac{(\eta^T v_i)^2}{v_i^T u_i} , \end{aligned}$

( 2.12)

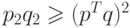поскольку $p_2 q_2 \geqslant (p^T q)^2$ согласно неравенству Шварца.

Знаменатель в соотношении (2.12) положителен, так как

$v_i^T u_i = v_i^T [g_{i+1} - g_i] = -v_i^T g_i,$

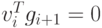поскольку $v_i^T g_{i+1} = 0$ из уравнения (2.4).

Следовательно,

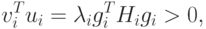
$v_i^T u_i = \lambda_i g_i^T H_i g_i > 0 ,$

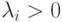так как $\lambda_i > 0$ и матрица H_i положительно определена.

Таким образом, 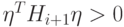$\eta^T H_{i+1} \eta > 0$ , что и доказывает положительную определенность матрицы Н_i+1.

б) Теперь покажем, что если метод ДФП применяется к квадратичной функции (с симметрической положительно определенной матрицей G, то Н_n = G^-1 и поиск минимума закончится через n шагов. Для доказательства достаточно показать, что v₀, v₁, ..., v_k - линейно независимые собственные векторы матрицы H_k+1G с собственными значениями, равными единице. Тогда матрица H_nG должна быть единичной.

Отметим, что из соотношения (2.5) следует, что

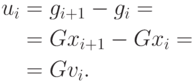$\begin{aligned} u_i & = g_{i+1} - g_i = \\ & = Gx_{i+1} - Gx_i = \\ & = Gv_i. \end{aligned}$

( 2.14)

Кроме того,

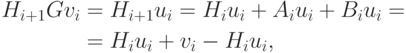
$\begin{aligned} H_{i+1} Gv_i & = H_{i+1} u_i = H_i u_i + A_i u_i + B_i u_i = \\ & = H_i u_i + v_i - H_i u_i, \end{aligned}$

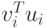что следует из соотношений (2.6) – (2.8) и из того, что v_i^T u_i

и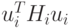

можно сократить.

Таким образом,

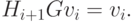$H_{i+1} Gv_i = v_i.$

( 2.15)

Далее методом индукции по k покажем, что для к = 2, 3, ..., n справедливы соотношения

$v_i^T Gv_j = 0 \; \text{при} \; 0 \leqslant i < j < k,$

( 2.16)

$H_k Gv_i = v_i \; \text{при} \; 0 \leqslant i < k,$

( 2.17)

Для доказательства в соотношении (2.15) положим i = 0 и получим H₁Gv₀ = v₀, т.е. соотношение (2.17) при k = 1. При k = 2 соотношение (2.17) будет иметь вид

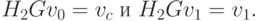
$H_2 Gv_0 = v_c \; \text{и } H_2 Gv_1 = v_1.$

Второе равенство следует из соотношения (2.15) при i = 1.

Для первого равенства имеем

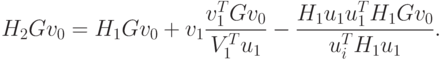
$H_2 Gv_0 = H_1 Gv_0 + v_1 \frac{v_1^T Gv_0}{V_1^T u_1} - \frac{H_1 u_1 u_1^T H_1 Gv_0}{u_i^T H_1 u_1} .$

Два последних члена в правой части равны нулю, поскольку

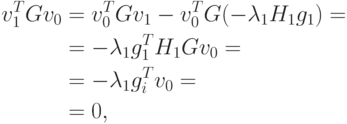
$\begin{aligned} v_1^T Gv_0 & = v_0^T Gv_1 - v_0^T G(-\lambda_1 H_1 g_1) = \\ & = -\lambda_1 g_1^T H_1 Gv_0 = \\ & = -\lambda_1 g_i^T v_0 = \\ & = 0, \end{aligned}$

что следует из соотношения (2.15) при i = 0 и из соотношения (2.4) при i = 0. Кроме того, u₁ = Gv₁, так что u_1^T H_1 Gv_0 = v_1^T Gv_0

. Таким образом, показано, что соотношение (2.17) справедливо при k = 2. После переноса в другую часть уравнения получим требуемый результат:

что является соотношением (2.6) при k = 2.

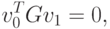
Теперь по индукции покажем, что если соотношения (2.16) и (2.17) справедливы при k, то они справедливы и при k + 1.

Имеем

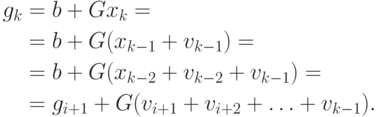$\begin{aligned} g_k & = b + Gx_k = \\ & = b + G(x_{k-1} + v_{k-1}) = \\ & = b + G(x_{k-2} + v_{k-2} + v_{k-1}) = \\ & = g_{i+1} + G(v_{i+1} + v_{i+2} + \ldots + v_{k-1}) . \end{aligned}$

( 2.18)

Из соотношения (2.16) при I < k — 1 получим

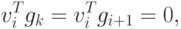
$v_i^T g_k = v_i^T g_{i+1} = 0,$

и из соотношения (2.4) непосредственно следует, что

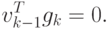
$v_{k-1}^T g_k = 0.$

Тогда

$v_i^T g_k = 0 \; \text{при } 0 \leqslant i < k ,$

( 2.19)

и из соотношения (2.17) следует, что

$v_i GH_k g_k = 0 \; \text{при } 0 \leqslant i < k ,$

причем

и

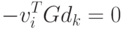
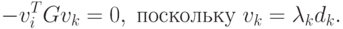
$-v_i^T Gv_k = 0, \; \text{поскольку } v_k = \lambda_k d_k.$

Следовательно,

$v_i^T Gv_k = 0 \; \text{при } 0 \leqslant i < k,$

( 2.20)

т.е.

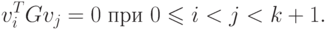$v_i^T Gv_j = 0 \; \text{при } 0 \leqslant i < j < k + 1.$

( 2.21)

Из соотношений (2.14) и (2.17) также имеем

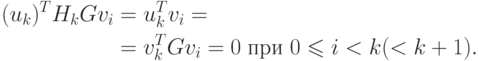$\begin{aligned} (u_k)^T H_k Gv_i & = u_k^T v_i = \\ & = v_k^T Gv_i = 0 \; \text{при } 0 \leqslant i < k (< k+1). \end{aligned}$

( 2.22)

Тогда из соотношений (2.6) – (2.17) следует

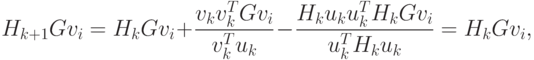
$H_{k+1} Gv_i = H_k Gv_i + \frac{v_k v_k^T Gv_i}{v_k^T u_k} - \frac{H_k u_k u_k^T H_k Gv_i}{u_k^T H_k u_k} = H_k Gv_i ,$

так как

и

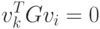
$u_k^T H_k Gv_i = u_k^T v_i = v_k^T Gv_i = 0 \; \text{при } 0 \leqslant i < k.$

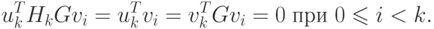
Таким образом, показано, что

$H_{k+1}Gv_i = H_k Gv_i = v_i \; \text{при } 0 \leqslant i < k.$

( 2.23)

При i = k имеем

$\begin{aligned} H_{k+1} Gv_k & = H_k Gv_k + \frac{v_k v_k^T Gv_k}{v_k^T u_k} - \frac{H_k u_k u_k^T H_k GV_k}{u_k^T H_k u_k} = \\ & = H_k u_k + v_k - H_k u_k , \end{aligned}$

поскольку

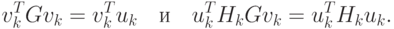
$v_k^T Gv_k = v_k^T u_k \quad \text{и} \quad u_k^T H_k Gv_k = u_k^T H_k u_k.$

Следовательно, H_k+1Gv_k = v_k и из соотношения (2.23) получаем

$H_{k+1} Gv_i = v_i \; \text{при } 0 \leqslant i < k+1 .$

( 2.24)

Соотношения (2.21) и (2.24) так же справедливы для следующего k, как и соотношения (2.16) и (2.17). Следовательно, доказательство по индукции закончено. Из соотношения (2.16) следует, что векторы v₀, v₁, ..., v_n-1 линейно независимы. Они являются взаимно сопряженными по отношению к матрице G. Из соотношения (2.17) следует, что v₀, v₁, ..., v_n-1 являются собственными векторами матрицы H_nG с собственным значением, равным единице. Тогда матрица H_nG должна быть единичной. Следовательно,

$H_n = G^{-1} .$

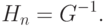( 2.25)

Из соотношения (2.19) следует, что минимум найден за n итераций. Вектор g_n должен быть ортогонален каждому из n независимых векторов v₀, v₁, ..., v_n-1. Следовательно,

( 2.26)

в) Способ обновления матрицы H описывается в соотношении (2.6):

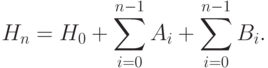
$H_n = H_0 + \sum_{i=0}^{n-1} A_i + \sum_{i=0}^{n-1} B_i .$

Покажем, что 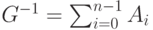$G^{-1} = \sum_{i=0}^{n-1} A_i$ . Из условий ортогональности (2.16) следует

V^TGV=D,

где V — матрица, состоящая из векторов vi, a D - диагональная матрица с элементами 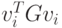v_i^T Gv_i .

Следовательно,

G=(V^T)^-1DV^-1

Тогда

G^-1=VDV^-1V^T,

а поскольку D - диагональная матрица, то можно произвести инверсию и перемножить матрицы для получения выражения

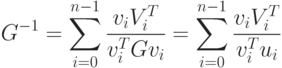
$G^{-1} = \sum_{i=0}^{n-1} \frac{v_i V_i^T}{v_i^T Gv_i} = \sum_{i=0}^{n-1} \frac{v_i V_i^T}{v_i^T u_i}$

(см. соотношение (2.14))

Таким образом,

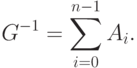$G^{-1}=\sum_{i=0}^{n-1} A_i .$

( 2.27)

Поскольку соотношение (2.15) должно выполняться, то Н_i+1Gv_i - V_i, а это означает, что v_i = H_iGv_i + A_iGv_i + B_iGv_i. Так как

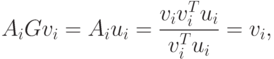
$A_i Gv_i = A_i u_i = \frac{v_i v_i^T u_i}{v_i^T u_i} = v_i ,$

то

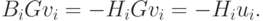( 2.28)

где z - произвольный вектор. Поскольку мы хотим, чтобы матрица B_i была симметрической, то выберем в качестве вектора z = Н_iu_i, такой, чтобы

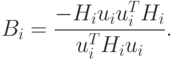$B_i = \frac{-H_i u_i u_i^T H_i}{u_i^T H_i u_i} .$

( 2.29)

Этим завершается теоретическое изложение метода ДФП, который использует как идеи метода Ньютона — Рафсона, так и свойство сопряженных направлений, и при применении для минимизации квадратичной функции n переменных он сходится не более чем за n итераций. Это весьма мощная оптимизационная процедура, очень эффективная при оптимизации большинства функций независимо от того, квадратичны они или нет.

Ниже приведена блок – схема данной процедуры.

Рис. 11.3.

Дальше >>

Введение в математическое программирование

Введение в математическое программирование

Лекция 11: Метод наискорейшего спуска. Метод Давидона – Флетчера – Пауэлла. Проблема оврагов. Проблема многоэкстремальности

2. Метод Давидона - Флетчера – Пауэлла

Вопросы и ответы

Студенты

Авторизоваться

Введение в математическое программирование

Введение в математическое программирование

Лекция 11: Метод наискорейшего спуска. Метод Давидона – Флетчера – Пауэлла. Проблема оврагов. Проблема многоэкстремальности

2. Метод Давидона - Флетчера – Пауэлла

Вопросы и ответы

Студенты