НОУ ИНТУИТ | Введение в математическое программирование. Лекция 1: Математическое моделирование. Математическая модель в задачах оптимизации. Элементарные математические модели

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.07.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Донецкий национальный технический университет

|

Вам нравится? Нравится 52 студентам

| Поделиться |

Поддержать программу

б) Сохранение материи. Именно этим соображением руководствуется школьник, решающий задачу о заполнении бассейна водой, втекающей и вытекающей из двух труб. Конечно же, область применения этого закона несравненно шире.

Пусть, например, имеется небольшое количество радиоактивного вещества (урана), окруженного толстым слоем "обычного" материала (свинца), — ситуация типичная либо при хранении делящихся материалов, либо при их использовании в энергетике (рис. 1.4).

Рис. 1.4.

Под словом "небольшой" подразумевается упрощающее обстоятельство, а именно то, что все продукты распада, не испытывая столкновений с атомами вещества, беспрепятственно покидают область I. Другими словами, длина свободного пробега продуктов распада $\lambda_I$ в первом веществе значительно больше характерных размеров самого материала L_I, Т.е. $\lambda_I \gg L_I$ . Слова "толстый слой" означают, что в согласии с целями хранения продукты деления полностью поглощаются в области II. 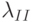Это гарантируется при выполнении противоположного условия $\lambda_{II} \ll L_{II}$ , где $\lambda_{II}$ — длина пробега продуктов распада во втором веществе, L_II — его характерный размер.

Итак, все, что вылетает из области I, поглощается в области II, и суммарная масса обоих веществ со временем не меняется. Это и есть закон сохранения материи, примененный к данной ситуации. Если в начальный момент времени t=0 массы веществ были равны M_I(0) и M_II(0), то в любой момент времени справедлив баланс

$M_I(0)+M_{II}(0)=M_I(t)+M_{II}(t).$

( 4)

Одного уравнения (4), очевидно, недостаточно для определения текущих значений двух масс - M_I(t) и M_II(t). Для замыкания математической формулировки необходимо привлечь дополнительное соображение о характере распада. Оно гласит, что скорость распада (число атомов, распадающихся в единицу времени) пропорционально общему числу атомов радиоактивного вещества. За небольшое время dt между моментами t и t + dt всего распадется

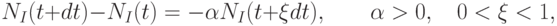
$N_I(t+dt)-N_I(t)=-\alpha N_I(t+\xi dt), \qquad \alpha > 0, \quad 0 < \xi < 1,$

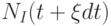атомов. Здесь вторично использован закон сохранения вещества, но применительно не ко всему процессу, а к отрезку времени dt. В этом уравнении, описывающем баланс атомов, в правой части стоит знак минус (вещество убывает), а величина $N_I(t + \xi dt)$ отвечает некоторому среднему значению числа атомов за рассматриваемое время. Перепишем его в дифференциальной форме:

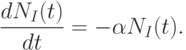
$\frac{dN_I(t)}{dt}=-\alpha N_I(t).$

Учитывая, что $M_I(t) = \mu_I N_I(t)$ , где $\mu_I$ — атомный вес вещества I, получаем

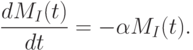$\frac{dM_I(t)}{dt}=-\alpha M_I(t).$

( 5)

При самопроизвольной радиоактивности любой атом имеет некоторую не зависящую от состояния окружающего вещества вероятность распада. Поэтому чем больше (меньше) самого радиоактивного вещества, тем больше (меньше) выделяется продуктов распада в единицу времени. Коэффициент пропорциональности 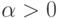$\alpha > 0$ ( постоянная распада ) определяется конкретным веществом.

Уравнения (4), (5) вместе с условиями $\lambda_I \gg L_I , \; \lambda_II \ll L_II$ , а также величинами $\alpha$ , M_I(0), M_II(0) и составляют математическую модель рассматриваемого объекта.

Интегрируя (5), получаем, что масса делящегося материала убывает по экспоненциальному закону

$M_I(t)=M_I(0)e^{-\alpha t},$

и при $t \rightarrow \infty$ в области I вещество полностью исчезает.

Так как суммарная масса в соответствии с (4) остается постоянной, то в области II количество вещества растет:

$M_{II}(t)=M_{II}(0)+M_I(0)-M_I(0)e^{-\alpha t}=M_{II}(0)+M_I(0)(1-e^{-\alpha t}),$

и при $t \rightarrow \infty$ продукты распада полностью переходят из области I в область II.

в) Сохранение импульса. Неподвижно стоящая в безветренную погоду на поверхности озера лодка начнет двигаться вперед, если сделать несколько шагов от ее носа к корме. Так проявляет себя закон сохранения импульса, утверждающий: полный импульс системы, не испытывающей действия внешних сил, сохраняется. На передвижение гребца лодка реагирует смещением в противоположную сторону.

Принцип реактивного движения положен в основу многих замечательных технических устройств, например, ракеты, выводящей на орбиту вокруг Земли искусственный спутник, для чего ей требуется развить скорость примерно 8 км/с. Простейшая математическая модель движения ракеты получается из закона сохранения импульса в пренебрежении сопротивлением воздуха, гравитацией и другими силами, исключая, конечно, тягу реактивных двигателей.

Пусть продукты сгорания ракетного топлива покидают расположенные в кормовой части выхлопные сопла со скоростью u (для современных топлив величина и равна 3-5 км/с). За малый промежуток времени dt между моментами t и t + dt часть топлива выгорела, и масса ракеты изменилась на величину dm. Изменился также импульс ракеты, однако суммарный импульс системы "ракета плюс продукты сгорания" остался тем же, что и в момент t, т.е.

$m(t)v(t)=m(t+dt)v(t+dt)-dm[v(t+\xi dt)-u],$

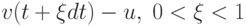где v(t) — скорость ракеты, $v(t + \xi dt) - u, \; 0 < \xi < 1$ - средняя за промежуток dt скорость истекающих из сопел газов (обе скорости берутся относительно Земли). Первый член в правой части этого равенства - импульс ракеты в момент t + dt, второй — импульс, переданный истекающим газом за время dt.

Учитывая, что m(t + dt) = m(t) + (dm/dt) dt + O(dt²), закон сохранения импульса можно переписать в виде дифференциального уравнения

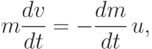
$m \frac{dv}{dt}=-\frac{dm}{dt} \, u,$

в котором член - (dm/dt) u, очевидно, не что иное, как сила тяги ракетных двигателей, и которое, будучи преобразованным к виду

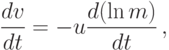
$\frac{dv}{dt}=-u \frac{d(\ln m)}{dt} \, ,$

легко интегрируется:

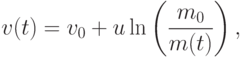
$v(t)=v_0+u \ln \left(\frac{m_0}{m(t)} \right),$

где v₀, m₀ - соответственно скорость и масса ракеты в момент t = 0. Если v₀=0, то максимальная скорость ракеты, достигаемая при полном сгорании топлива, равна

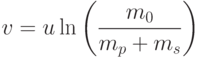$v=u \ln \left( \frac{m_0}{m_p+m_s} \right)$

( 6)

Здесь m_p - полезная масса (масса спутника), m_s - структурная масса (масса собственно ракетной конструкции - топливных баков, двигателей, систем управления и т.д.).

Простая формула Циолковского (6) позволяет сделать фундаментальный вывод о конструкции ракеты для космических полетов. Введем величину

$\lambda= \frac{m_s}{m_0-m_p},$

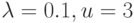которая характеризует при m_р = 0 отношение структурной и начальной масс ракеты. Тогда для практически реальных значений $\lambda = 0.1, u = 3$ км/с получаем при m_р = 0

$v=u \ln \frac{1}{\lambda} = 7 км/с,$

Отсюда следует, что даже в самой идеальной ситуации (полезная масса равна нулю, отсутствуют гравитация и сопротивление воздуха и т.д.) ракета рассматриваемого типа не способна достичь первой космической скорости. Тем самым необходимо использовать многоступенчатые ракеты - вывод, к которому пришли основоположники космонавтики.

Данный пример иллюстрирует также своего рода принцип "наибольшего благоприятствия", часто используемый на начальной стадии математического моделирования сложных объектов: если объект, поставленный в наилучшие условия, не в состоянии достичь требуемых характеристик, то надо изменить сам подход к объекту либо смягчить требования к нему; если же требования в принципе достижимы, то следующие шаги связаны с исследованием влияния на объект дополнительных осложняющих факторов.

Дальше >>

Введение в математическое программирование

Введение в математическое программирование

Математическое моделирование. Математическая модель в задачах оптимизации. Элементарные математические модели

Вопросы и ответы

Студенты

Авторизоваться

Введение в математическое программирование

Введение в математическое программирование

Математическое моделирование. Математическая модель в задачах оптимизации. Элементарные математические модели

Вопросы и ответы

Студенты