Компьютерное моделирование и решение нелинейных уравнений

Метод Рунге - Кутта 2-го порядка (модифицированный метод Эйлера)

Отбросим в (12.4) члены ряда, содержащие h₃, h₄, h₅:.

Тогда

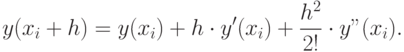( 12.6)

Чтобы сохранить член ряда, содержащий h², надо определить вторую производную y"(x_i).Ее можно аппроксимировать разделенной разностью 2-го порядка

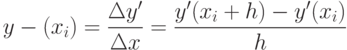
Подставляя это выражение в (12.6), получим

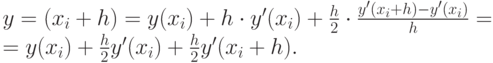
Окончательно, модифицированная или уточненная формула Эйлера имеет вид:

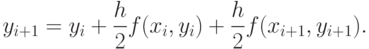( 12.7)

Как видно, для определения функции y(x) в точке i+1 необходимо знать значение правой части дифференциального уравнения f(x_i+1, y_i+1) в этой точке, для определения которой необходимо знать предварительное значение y_i+1.

Для определения предварительного значения y_i+1 воспользуемся формулой Эйлера. Тогда все вычисления на каждом шаге по модифицированной или уточненной формуле Эйлера будем выполнять в два этапа:

На первом этапе вычисляем предварительное значение по формуле Эйлера

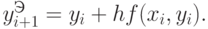
На втором этапе уточняем значение y=_i+1 по модифицированной или уточненной формуле Эйлера

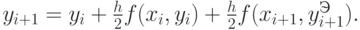
Точность метода определяется отброшенными членами ряда Тейлора (12.4), т.е. точность уточненного или модифицированного метода Эйлера на каждом шаге .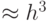

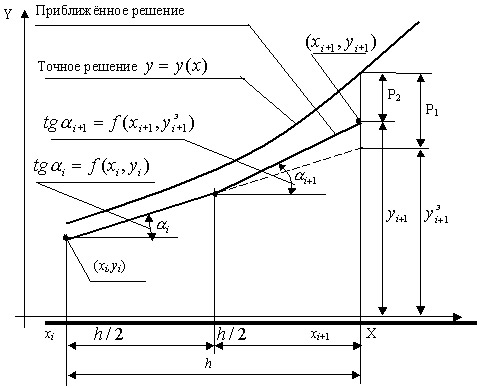
Рассмотрим геометрический смысл модифицированного метода Эйлера.

Так как

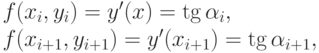
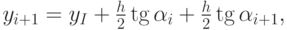
где

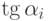- тангенс угла наклона касательной к искомой функции у(х) в начальной точке каждого шага,

- тангенс угла наклона касательной к искомой функции у(х) в конечной точке каждого шага.

Рис. 12.12. Геометрический смысл модифицированного метода Эйлера

Здесь

P₁ - накопленная ошибка в (i+1)^й точке по методу Эйлера,

P₂ - накопленная ошибка в (i+1)^й точке по модифицированному методу Эйлера.

Как видно из рис.12.11, в первой половине каждого шага, то есть на участке [x_i, x_i+h/2], искомая функция y(x) аппроксимируется прямой, которая выходит из точки (x_i, y_i) под углом, тангенс которого .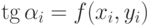

Во второй половине этого же шага, т.е. на участке [x_i + h/2,x_i + h], искомая функция y(x) аппроксимируется прямой, которая выходит из точки с координатами

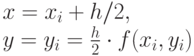
под углом, тангенс которого

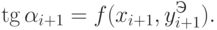
В результате в модифицированном методе Эйлера функция у(х) на каждом шаге аппроксимируется не одной прямой, а двумя.

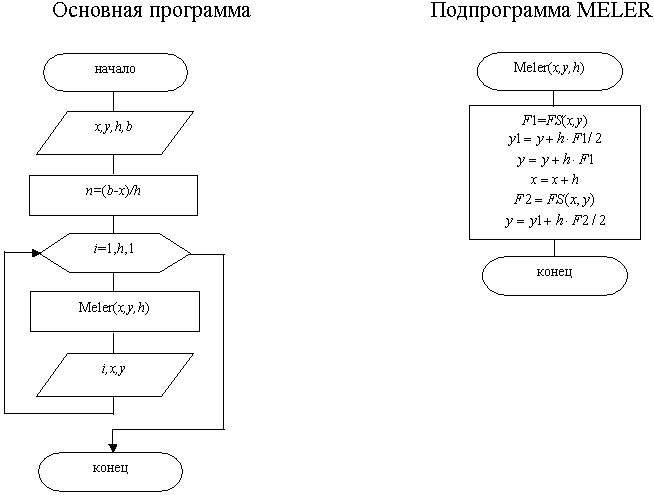
Алгоритм модифицированного метода Эйлера можно построить в виде двух программных модулей: основной программы и подпрограммы МELER, реализующей метод (рис. 12.13).

Рис. 12.13. Схема алгоритма модифицированного метода Эйлера

Здесь

(x,y) -при вводе начальная точка, далее текущие значения табличной функции,

h -шаг интегрирования дифференциального уравнения,

b -конец интервала интегрирования.