|
В уравнениях движения кривошипно-шатунного механизма вместо обозначения радиуса кривошипа "r" ошибочно записан символ "?" (гамма). P.S. Может быть это слишком очевидно, но не упомянуто, что угол поворота кривошипа ? считается малым. |
Компьютерное моделирование и решение линейных и нелинейных многомерных систем
При моделировании экономических задач, таких как задачи управления и планирования производства, определения оптимального размещения оборудования, оптимального плана производства, оптимального плана перевозок грузов (транспортная задача), распределения кадров и др., может быть положена гипотеза линейного представления реального мира.
Математические модели таких задач представляются линейными уравнениями. Если задача многомерна, то ее математическая модель представляется системой линейных уравнений.
Линейные математические модели также используются в нелинейных системах при условии, если эта нелинейная система условно линеаризирована.
В общем виде система линейных уравнений имеет вид:
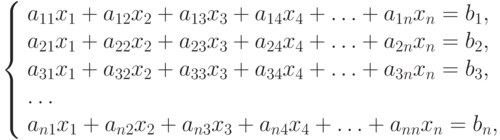
где
aij - коэффициенты при неизвестных системы,
xj - неизвестные системы,
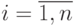 - номер строки,
- номер строки,
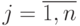 - номер столбца,
- номер столбца,
n - порядок системы.
В матричной форме система линейных уравнений имеет вид:
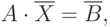
где
![{A} = \left [\begin{array}{ccc} a_{11} a_{12} \ldots a_{1n}\\
a_{21} a_{22} \ldots a_{2n}\\
\ldots \ldots \ldots \ldots\\
a_{n1} a_{n2} \ldots a_{nn}\\
\end{array} \right] \text{ –матрица коэффициентов системы порядка } {(n \times n)},](/sites/default/files/tex_cache/47d99f3dadf244d749195c600384371b.png)
![\mathbf{\overline X} = \left[ \begin{array}{ccc} x_1\\ x_2\\ \ldots\\ x_n\\ \end{array} \right] \text{ – вектор неизвестных системы размерностью n},](/sites/default/files/tex_cache/c7d69f22e1febfdcd3813516c4d049a7.png)
![\mathbf{\overline B} = \left[ \begin{array}{ccc} b_1\\ b_2\\ \ldots\\ b_n\\ \end{array} \right] \text{ – вектор свободных членов размерностью n}.](/sites/default/files/tex_cache/c7afd587471cd76a3fe656036f9d33d8.png)
Численные методы решения систем линейных уравнений (СЛУ) можно разделить на две группы:
- точные или прямые методы,
- приближенные методы.
Приближенные методы реализуют на ЭВМ нахождение корней с заданной точностью и являются итерационными методами.
Точные методы позволяют получить решение системы за конечное число итераций. К точным методам относятся:
Решение систем линейных уравнений методом Гаусса
Метод Гаусса является точным методом. Он позволяет получить решение системы за конечное число арифметических действий. В основе метода лежит идея последовательного исключения неизвестных. Метод состоит из двух этапов. На первом этапе (прямой ход) система при помощи последовательного исключения неизвестных приводится к треугольному виду. На втором этапе (обратный ход) из системы треугольного вида последовательно, в обратном порядке, начиная c n-го уравнения, находятся неизвестные системы.
В качестве примера возьмем систему 4 порядка.
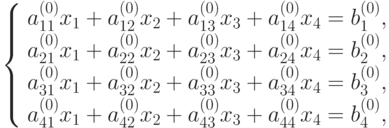 |
( 9.1) |
Прямой ход. На первом шаге прямого хода (к=1) находим x1 из первого уравнения системы (9.1).
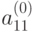 - ведущий элемент первой строки.
- ведущий элемент первой строки.
Если 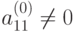 , то
, то
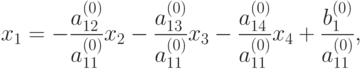 |
( 9.2) |
Обозначим:
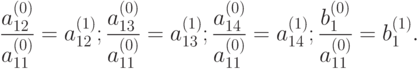 |
( 9.3) |
Подставляя (9.3) в (9.2), получим
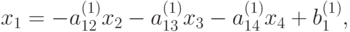 |
( 9.4) |
где
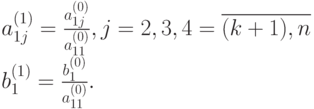
Подставляем (9.4) во 2, 3 и 4 уравнение системы (9.1), получим:
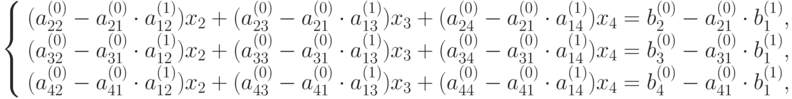
Обозначив коэффициенты при неизвестных полученной системы через 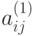 , а свободные члены через
, а свободные члены через 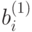 перепишем полученную систему:
перепишем полученную систему:
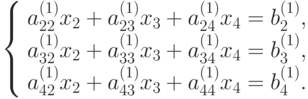 |
( 9.5) |
где
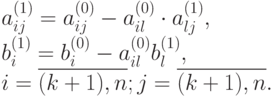
Таким образом, в результате выполнения первого шага прямого хода исходная система (9.1) n-го порядка преобразована к совокупности уравнения (9.4) и системы линейных уравнений (9.5), порядок которой равен n-1.
На втором шаге прямого хода (к=2) из первого уравнения системы (9.5) находим x2.
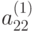 -ведущий элемент первой строки системы (9.5).
-ведущий элемент первой строки системы (9.5).
Если 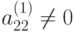 , то из первого уравнения системы (9.5) имеем:
, то из первого уравнения системы (9.5) имеем:
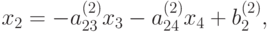 |
( 9.6) |
где
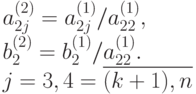
Подставив выражение (9.6) во второе и третье уравнения системы (9.5), получим новую систему линейных уравнений, порядок которой равен n-2.
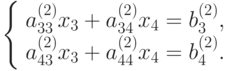 |
( 9.7) |
где
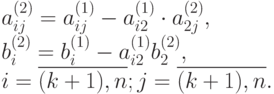
Таким образом, в результате выполнения второго шага прямого хода исходная система (9.1) преобразована к совокупности уравнений (9.4), (9.6) и системы линейных уравнений (9.7),порядок которой равен n-2.
