|
В уравнениях движения кривошипно-шатунного механизма вместо обозначения радиуса кривошипа "r" ошибочно записан символ "?" (гамма). P.S. Может быть это слишком очевидно, но не упомянуто, что угол поворота кривошипа ? считается малым. |
Компьютерное моделирование и решение нелинейных уравнений
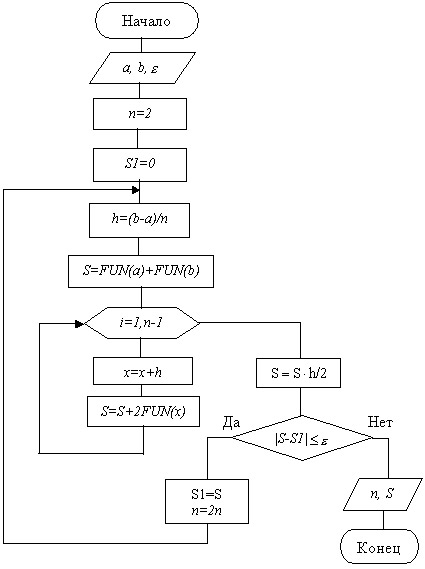
Метод трапеций
Словесный алгоритм метода трапеций:
- Интервал [a,b] делим на n равных частей с шагом h=(b-a)/n.
- Вычисляем значение подынтегральной функции в каждой узловой точке
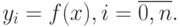
- На каждом шаге подынтегральную функцию f(x) аппроксимируем прямой, соединяющей две соседние узловые точки. В результате вся подынтегральная функция на участке [a,b] заменяется ломаной линией проходящей через все узловые точки.
- Вычисляем площадь каждой частичной трапеции.
- Приближенное значение интеграла равно сумме площадей частичных трапеций, т.е.
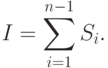
Найдем площади Si частичных трапеций:
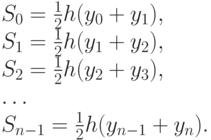
Приближенное значение интеграла равно
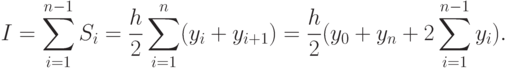
Точность метода трапеций имеет порядок h2.
Схема алгоритма метода трапеций представлена на рис.12.6.
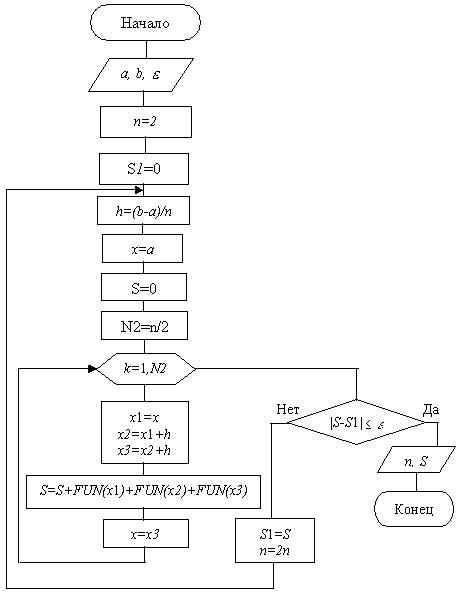
Метод Симпсона
В методе Симпсона в каждой части деления подынтегральная функция аппроксимируется квадратичной параболой a0x2+a1x+a2. В результате вся кривая подынтегральной функции на участке [a,b] заменяется кусочно-непрерывной линией, состоящей из отрезков квадратичных парабол. Приближенное значение интеграла I равно сумме площадей под квадратичными параболами.
Т.к. для построения квадратичной параболы необходимо иметь три точки, то каждая часть деления в методе Симпсона включает два шага, т.е.
Lk=2h.
В результате количество частей деления N2=n/2. Тогда n в методе Симпсона всегда четное число.
Определим площадь S1 на участке [x0, x2] (рис.12.2).
Исходя из геометрического смысла определенного интеграла, площадь S1 равна определенному интегралу от квадратичной параболы на участке [x0, x2]:
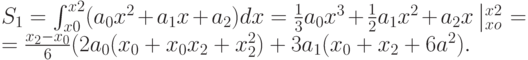
Неизвестные коэффициенты квадратичной параболы а0 , а1, а2 определяем из условия прохождения параболой через три узловых точки с координатами (x0y0), (x1y1), (x2y2).
На основании этого условия строим систему линейных уравнений:
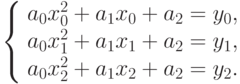
Решая эту систему, найдем коэффициенты параболы.
В результате имеем: 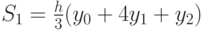 ..
..
Для участка [x2, x4]: 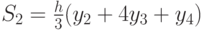 ..
..
:::::::::::::::::::
Для участка [xi-1, xi+1]: 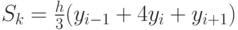 .,
.,
где 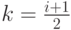 .
.
Суммируя все площади S1 под квадратичными параболами, получим квадратурную формулу по методу Симпсона:
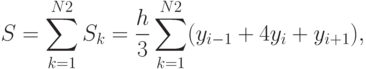
где
N2 - количество частей деления.
Точность метода Симпсона имеет порядок (h3/h4).
Схема алгоритма метода Симпсона представлена на рис.12.7.