|
Здравствуйте Владимир (Ефименко). Я обучаюсь по программе повышения квалификации "Наноэлектронная элементная база информатики на основе полупроводников и ферромагнетиков". У меня проблема с тестом № 2 (к лекции № 2) по этой программе. Я несколько раз пытался пройти этот тест, но больше 50 баллов набрать не удаётся, хотя я всё делаю в соответствии сматериалом лекции. В заданиях этого теста есть ошибки, которые видны невооружённым глазом. Обращаюсь к Вам как к инспектору этой программы повышения квалификации. Найдите возможность исправить ошибки в тесте № 2. Из-за остановки на этом тесте я не могу двигаться дальше, а у меня очень ограниченное время на освоение этой программы. Заранее благодарен Вам за внимание к моим проблемам и помощь. |
Качественные изменения свойств при переходе к наноразмерным элементам
Явления квантовой интерференции
Мы уже знаем, что квантовая механика описывает свободные электроны как волны, которые распределены и распространяются по всему проводнику или полупроводнику. Как волны, они характеризуются своими скоростью распространения (или волновым вектором), частотой (или длиной волны), амплитудой и фазой. Если волна распространяется свободно, то разные ее части остаются когерентными, т.е. могут интерферировать между собой. При неупругих рассеяниях когерентность теряется. Среднее расстояние, которое электронная волна проходит, сохраняя когерентность, называют длиной когерентности.
На рис. 3.11 слева показан проводящий (полупроводниковый) элемент, который имеет вход, разветвление (1 и 2) и выход. Если размеры элемента меньше длины когерентности, то электронная волна, распространяясь вдоль ветвей 1 и 2, сохраняет когерентность, благодаря чему ее части, объединяясь на выходе, могут интерферировать. Результат интерференции зависит от разности их фаз: если фазы противоположны, то электронные волны, встречаясь, гасят одна другую, и электрический ток на выходе близок к нулю. Если же фазы совпадают, то электронные волны усиливают одна другую, и электрический ток на выходе максимальный.
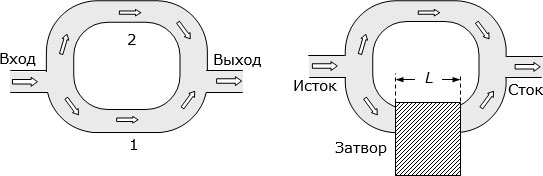
Рис. 3.11. Слева – топология элемента с квантовой интерференцией. Справа – конструкция интерференционного транзистора
Разность фаз электронных волн, распространяющихся вдоль разных ветвей структуры, может зависеть от различных факторов. Например, если над одной из ветвей нанести тонкий слой диэлектрика и сформировать на нем электрод затвора, то электрическое поле этого затвора будет несколько изменять волновой вектор электронов.
В результате между электронными волнами, которые приходят к стоку, возникнет разность фаз
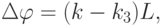 |
( 3.31) |
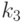 – волновой вектор электронов в подзатворной области (он зависит от напряжения на затворе),
– волновой вектор электронов в подзатворной области (он зависит от напряжения на затворе),  – волновой вектор во всех других местах,
– волновой вектор во всех других местах,  – длина пути, который проходят электроны под затвором. Такую структуру называют квантовым интерференционным транзистором (англ. quantum interference transistor). Электрический ток стока синусоидально зависит в нем от потенциала затвора.
– длина пути, который проходят электроны под затвором. Такую структуру называют квантовым интерференционным транзистором (англ. quantum interference transistor). Электрический ток стока синусоидально зависит в нем от потенциала затвора.Другой вариант квантового интерференционного транзистора показан на рис. 3.12 слева. Электронная волна от истока разделяется на 2 части. Одна движется к стоку коротким путем (1), а другая (2) сначала движется к затвору.
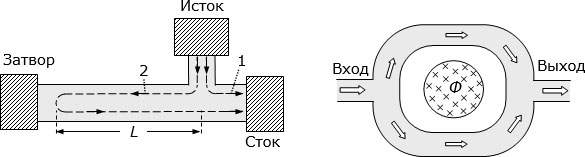
Рис. 3.12. Слева – другая конструкция интерференционного транзистора. Справа – схема наблюдения эффекта Ааронова–Бома
Когда к затвору приложено отрицательное напряжение, то электроны отталкиваются электрическим полем и поэтому, не доходя до затвора, электронная волна отражается и движется в противоположном направлении. На электроде стока электронные волны 1 и 2 интерферируют. Результат интерференции зависит от разности фаз между ними, а она, в свою очередь, зависит от расстояния  . Расстояние это тем меньше, чем больше по абсолютной величине отрицательный потенциал на затворе. Незначительные изменения этого потенциала могут приводить к значительным изменениям тока стока.
. Расстояние это тем меньше, чем больше по абсолютной величине отрицательный потенциал на затворе. Незначительные изменения этого потенциала могут приводить к значительным изменениям тока стока.
В обоих вариантах квантовый интерференционный транзистор может иметь значительный коэффициент усиления и высокое быстродействие. Ведь скорость электронных волн 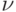 достаточно велика, а расстояния – порядка нанометров. Например, в арсениде галлия
достаточно велика, а расстояния – порядка нанометров. Например, в арсениде галлия 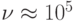 м/с, и при
м/с, и при  нм время распространения волны от истока к стоку составляет порядка
нм время распространения волны от истока к стоку составляет порядка 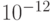 с. Поэтому соответствующая частота переключений транзистора теоретически может быть порядка сотен гигагерц. Практически же предельная частота зависит от "паразитных" параметров схемы, в первую очередь, от времени перезарядки электрических емкостей затвора и стока.
с. Поэтому соответствующая частота переключений транзистора теоретически может быть порядка сотен гигагерц. Практически же предельная частота зависит от "паразитных" параметров схемы, в первую очередь, от времени перезарядки электрических емкостей затвора и стока.
Еще одним фактором получения разности фаз электронных волн, распространяющихся вдоль различных ветвей проводника, и управления величиной тока на выходе может служить магнитное поле ( рис. 3.12 справа). В условиях существования квантовой интерференции в замкнутом проводящем или полупроводниковом кольце (контуре) оказываются допустимыми лишь такие электронные волны, при которых сквозь отверстие контура проникает целое число квантов магнитного потока
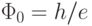 |
( 3.32) |
 – постоянная Планка,
– постоянная Планка,  – электрический заряд электрона. Если внешнее магнитное поле создает магнитный поток
– электрический заряд электрона. Если внешнее магнитное поле создает магнитный поток  , который не равняется целому числу квантов, то в контуре возникает дополнительный циркулирующий ток, который создает магнитный поток сквозь отверстие контура, равный разности
, который не равняется целому числу квантов, то в контуре возникает дополнительный циркулирующий ток, который создает магнитный поток сквозь отверстие контура, равный разности  . А это приводит к сдвигу фаз между электронными волнами, которые распространяются вдоль разных ветвей контура, на величину
. А это приводит к сдвигу фаз между электронными волнами, которые распространяются вдоль разных ветвей контура, на величину
 |
( 3.33) |
Описанные количественное и качественное изменения свойств наноразмерных элементов создают предпосылки для разработки новых схемотехнических принципов и концепций построения наноэлектронной элементной базы информатики.
