|
Здравствуйте Владимир (Ефименко). Я обучаюсь по программе повышения квалификации "Наноэлектронная элементная база информатики на основе полупроводников и ферромагнетиков". У меня проблема с тестом № 2 (к лекции № 2) по этой программе. Я несколько раз пытался пройти этот тест, но больше 50 баллов набрать не удаётся, хотя я всё делаю в соответствии сматериалом лекции. В заданиях этого теста есть ошибки, которые видны невооружённым глазом. Обращаюсь к Вам как к инспектору этой программы повышения квалификации. Найдите возможность исправить ошибки в тесте № 2. Из-за остановки на этом тесте я не могу двигаться дальше, а у меня очень ограниченное время на освоение этой программы. Заранее благодарен Вам за внимание к моим проблемам и помощь. |
Качественные изменения свойств при переходе к наноразмерным элементам
Квантовая линия
Если наноэлемент имеет размеры меньше длины волны де Бройля в двух разных направлениях, то такие наноразмерные элементы называют "квантовой линией", хотя используют и другие названия – "квантовая нить", квантовая проволока (англ. quantum wires), квантовая трубка, нанотрубка и т.п. Для идеализированной квантовой линии с прямоугольным распределением потенциала, как на рис. 3.3, но уже в двух направлениях, которое математически описывается выражением
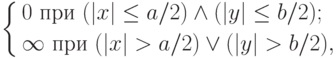 |
( 3.11) |
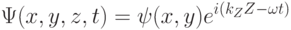 |
( 3.12) |
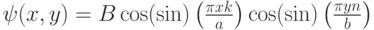 ;
; 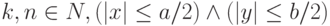 ,
,  – постоянный множитель, который определяется из условия нормирования волновой функции.
– постоянный множитель, который определяется из условия нормирования волновой функции.Решение существует лишь при целых значениях двух квантовых чисел  и
и  . В формуле следует использовать косинус, если соответствующее целое число не является четным, или синус – когда оно четное. Квантуются уже две компоненты импульса, которые могут принимать лишь значения:
. В формуле следует использовать косинус, если соответствующее целое число не является четным, или синус – когда оно четное. Квантуются уже две компоненты импульса, которые могут принимать лишь значения:
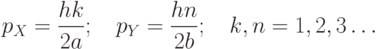 |
( 3.13) |
 и
и  потенциальной ямы при этом укладывается тоже целое число полуволн.
потенциальной ямы при этом укладывается тоже целое число полуволн.Кинетическая энергия электрона в потенциальной яме зависит здесь уже от значений двух квантовых чисел  и
и  :
:
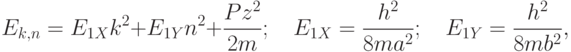 |
( 3.14) |
 – эффективная масса электрона.
– эффективная масса электрона.Даже когда электрон не движется вдоль квантовой линии (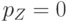 ), он имеет минимальную энергию
), он имеет минимальную энергию  и представляет собой стоячую волну с пучностью при
и представляет собой стоячую волну с пучностью при 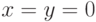 , т.е. на оси квантовой линии.
, т.е. на оси квантовой линии.
Компонента импульса 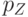 (направленная вдоль линии) не квантуется, т.е. может принимать любые непрерывные значения. При рассеяниях электрона на неоднородностях может изменяться лишь эта компонента импульса, т.е. электрон внутри квантовой линии ведет себя как одномерная частица-волна. А квантовая линия (квантовая нить, нанопроволока, нанотрубка) ведет себя как волновод.
(направленная вдоль линии) не квантуется, т.е. может принимать любые непрерывные значения. При рассеяниях электрона на неоднородностях может изменяться лишь эта компонента импульса, т.е. электрон внутри квантовой линии ведет себя как одномерная частица-волна. А квантовая линия (квантовая нить, нанопроволока, нанотрубка) ведет себя как волновод.
Если квантовая линия имеет длину меньше длины свободного пробега электронов в ней, тогда наблюдается еще один квантовый эффект. На
рис.
3.5 слева показана квантовая линия КЛ с присоединенными к ней электродами Эл1 и Эл2. Справа показана соответствующая энергетическая диаграмма в случае, когда между электродами создана разность потенциалов  . Вдоль вертикали отложена энергия электронов, вдоль горизонтали – координата.
. Вдоль вертикали отложена энергия электронов, вдоль горизонтали – координата.
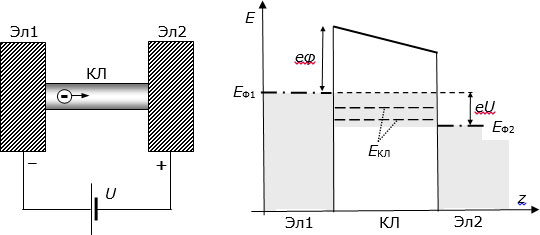
Рис. 3.5. Слева – квантовая линия, сквозь которую пропускают электрический ток; справа – энергетическая диаграмма такого соединения
Уровень Ферми 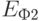 в электроде Эл2, к которому приложен положительный потенциал, снижается на величину
в электроде Эл2, к которому приложен положительный потенциал, снижается на величину 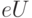 относительно уровня Ферми
относительно уровня Ферми  в электроде Эл1. Через
в электроде Эл1. Через 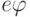 обозначена работа выхода электрона из электрода. При сверхнизких температурах, когда тепловой энергией электронов можно пренебречь, в переносе заряда между электродами Эл1 и Эл2 могут принимать участие лишь те электроны квантовой линии КЛ, разрешенные энергетические уровни которых лежат между
обозначена работа выхода электрона из электрода. При сверхнизких температурах, когда тепловой энергией электронов можно пренебречь, в переносе заряда между электродами Эл1 и Эл2 могут принимать участие лишь те электроны квантовой линии КЛ, разрешенные энергетические уровни которых лежат между  и
и 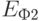 . Поскольку такие электроны "пролетают" сквозь всю квантовую линию без рассеяний, то, как показывает расчет, ее электрическое сопротивление перестает зависеть от размеров квантовой линии, включая длину, и равняется
. Поскольку такие электроны "пролетают" сквозь всю квантовую линию без рассеяний, то, как показывает расчет, ее электрическое сопротивление перестает зависеть от размеров квантовой линии, включая длину, и равняется
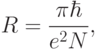 |
( 3.15) |
 – электрический заряд электрона,
– электрический заряд электрона,  – количество разрешенных квантовых состояний с энергией между уровнями Ферми в электродах.
– количество разрешенных квантовых состояний с энергией между уровнями Ферми в электродах.Величину 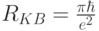 , приблизительно равную 6,45 кОм, называют "квантом электрического сопротивления", а обратную ей величину – "квантом электропроводности".
, приблизительно равную 6,45 кОм, называют "квантом электрического сопротивления", а обратную ей величину – "квантом электропроводности".
При комнатных температурах, когда электроны в квантовой линии имеют довольно широкий непрерывный спектр энергий, электрическое сопротивление квантовой линии практически определяется лишь электрическим сопротивлением контактов.
Квантовые точки
Наряду с квантовыми плоскостями и квантовыми линиями, которые называют соответственно "двумерными" и "одномерными" объектами, существуют также "нуль-мерные" объекты – потенциальные ямы, все три размера которых меньше длины волны де Бройля. Такие объекты называют "квантовыми точками" (англ. quantum dots). Для идеальных квантовых точек (с бесконечно глубокой потенциальной ямой прямоугольной формы) решение задачи Коши для уравнения Шредингера имеет вид:
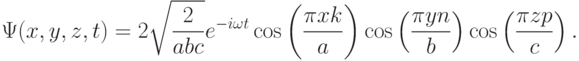 |
( 3.16) |
Решение существует лишь при целых значениях трех квантовых чисел  ,
,  и
и  (причем, как и раньше, косинус в этой формуле используют при нечетных значениях соответствующего квантового числа, а при четном значении используют синус). Это означает, что квантуются уже все три компоненты импульса, которые могут принимать лишь значения:
(причем, как и раньше, косинус в этой формуле используют при нечетных значениях соответствующего квантового числа, а при четном значении используют синус). Это означает, что квантуются уже все три компоненты импульса, которые могут принимать лишь значения:
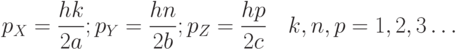 |
( 3.17) |
 ,
,  и
и  потенциальной ямы при этом укладывается тоже целое число полуволн.
потенциальной ямы при этом укладывается тоже целое число полуволн.Кинетическая энергия электрона в квантовой точке зависит от значений трех квантовых чисел  ,
,  и
и  :
:
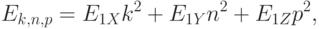
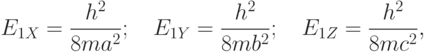 |
( 3.18) |
 – эффективная масса электрона.
– эффективная масса электрона.Поскольку энергетический спектр квантовых точек является уже целиком дискретным, то их иногда называют "искусственными атомами". Энергетический спектр, как видим, очень зависит от размеров квантовой точки. Как и в атомах, некоторые энергетические уровни могут совпадать, т.е. будут "вырожденными".
В реальных квантовых точках потенциальная яма не является прямоугольной, и потому решения квантовой задачи можно получить лишь посредством компьютерных вычислений. Но общий вывод о дискретности энергетического спектра остается верным и для них. Число допустимых энергетических уровней в реальных квантовых точках ограничено. Эти уровни можно изменять, контролируя пространственные размеры и форму квантовой точки или изменяя ее окружение (и соответственно перепад и распределение потенциала на краях квантовой ямы). На краях реальных квантовых точек волновая функция не обращается в нуль, т.е. электронное "облако" квантовой точки простирается и на некоторую ее окрестность.
Заметим еще, что квантовые плоскости, квантовые линии и квантовые точки все вместе теперь принято называть "низкоразмерными системами" или "системами пониженной размерности" – двумерными, одномерными и нуль-мерными.
