Классические шифры

6.7 Преобразования биграмм

Предположим теперь, что элементами открытого и шифрованного текстов являются двухбуквенные блоки, называемые биграммами. Это значит, что открытый текст разбивается на двухбуквенные сегменты. Если открытый текст состоит из нечётного числа букв, то, чтобы получить целое число биграмм, добавим к концу текста ещё одну букву, выбрав её так, чтобы не исказить смысл, например, добавим пробел, если он содержится в нашем алфавите.

Каждой биграмме приписывается далее её числовой эквивалент. Простейший способ - взять его в виде , где -числовой эквивалент первой буквы биграммы, -числовой эквивалент второй буквы биграммы, а -число букв в алфавите. Таким образом, мы рассматриваем биграмму, как запись двузначного числа в системе счисления с основанием . Это даёт взаимно однозначное соответствие между множеством всех биграмм в $N$-буквенном алфавите и множеством всех неотрицательных целых, меньших .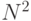

Следующий шаг - выбор шифрующего преобразования, т. е. перестановки целых чисел 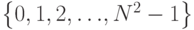. Примером простейших шифрующих преобразований служат аффинные преобразования: при шифровании переходит в неотрицательное целое число, меньшее 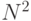и удовлетворяющее сравнению 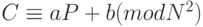. Здесь, как и раньше, число должно не иметь общих множителей с (что означает отсутствие общих множителей и с 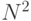) для того, чтобы существовало обратное преобразование.

Пример 6.9 Пусть мы имеем дело с 33-буквенным алфавитом и используем биграммное шифрующее преобразование . Тогда биграмма "НО" имеет числовой эквивалент 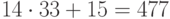, и ей соответствует биграмма шифртекста , то есть "ИЮ". Биграмма "ОН" имеет числовой эквивалент 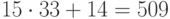, и ей соответствует биграмма шифртекста 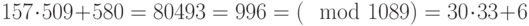, то есть "ЭЁ". Заметим, что биграмма преобразуется как единое целое, и между зашифрованными биграммами, имеющими общую букву или даже составленными из одних и тех же букв, но в разном порядке, нет явной связи.

Для вскрытия биграммной системы, использующей аффинное преобразование , надо знать элементы шифртекста, соответствующие двум разным элементам открытого текста. Так как элементами текста являются биграммы, то частотный анализ означает выделение в длинном отрезке шифртекста двухбуквенных блоков, встречающихся чаще других (разумеется, надо считать только элементы текста и игнорировать пары, образованные буквами соседних элементов), и сравнение с известными частотами биграмм в английских текстах, записанных в том же алфавите. Например, если используется 26-буквенный алфавит, то статистический анализ, скорее всего, покажет, что наиболее частыми биграммами являются "T H" и "H E" (в указанном порядке). Информации о двух парах отвечающих друг другу биграмм открытого и шифрованного текстов зачастую (но не всегда) бывает достаточно для определения и .

Пример 6.10 Вы знаете, что ваш противник использует криптосистему с 27-буквенным алфавитом, в котором буквы A-Z имеют числовые эквиваленты 0-25, и пробел=26. Каждой биграмме отвечает числовой эквивалент - целое число между 0 и 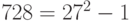, определяемое по правилу - числовые эквиваленты букв биграммы. Пусть анализ длинного шифртекста показал, что чаще всего в нём встречаются биграммы "Z A", "I A" и "I W" (в указанном порядке). Предположим, что самыми частыми биграммами в английском языке (в текстах в нашем 27-буквенном алфавите) являются биграммы "E_" (т. е. E и пробел), "S_" и "_T". Мы знаем, что криптосистема использует аффинное шифрующее преобразование по модулю 729. Найти ключ расшифрования и прочитать сообщение "NDXBHO". Найти также ключ шифрования.

Решение. Мы знаем, что открытый текст шифруется по правилу 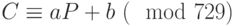, и что шифртекст может быть расшифрован по правилу 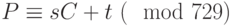, где , образуют ключ шифрования, а , - ключ расшифрования. Сначала мы хотим найти и . Нам известно, как расшифровываются три биграммы. Заменив эти биграммы их числовыми эквивалентами, получим три сравнения

Если исключить , взяв разность первых двух сравнений, то получим 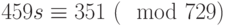, что не даёт единственного решения по модулю 729 (имеется 27 решений). Будет лучше, если вычесть из первого сравнения третье, что даст 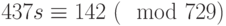. Для решения последнего сравнения надо найти число, обратное к 437 по модулю 729. Воспользуемся алгоритмом Евклида:

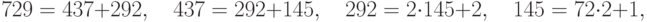
и затем .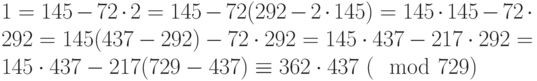

Итак, 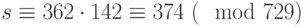, и, следовательно, 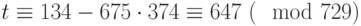. Теперь применим преобразование дешифрования к биграммам "N D", "X B" и "H O" нашего сообщения (им соответствуют целые числа 354, 622 и 203 соответственно) и получим числа 365, 724 и 24. Записав 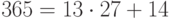, , 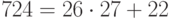, 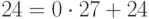мы соединим биграммы открытого текста в сообщение "NO WAY". Наконец, для нахождения ключа шифрования мы вычисляем (снова используя алгоритм Евклида) и .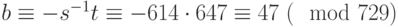

6.7.1 Шифрующие матрицы

Пусть имеется -буквенный алфавит, и блоками сообщения являются биграммы. Ранее мы каждой биграмме сопоставляли целое число по модулю 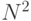, т.е. элемент кольца . Другой подход заключается в том, чтобы сопоставлять биграмме вектор 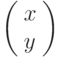с целыми числами и , рассматриваемыми по модулю . Например, если используется русский алфавит из 33 букв, то биграмме ОН соответствует вектор 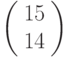(нумерация начинается с нуля, так что буква А имеет номер 0, буква Я имеет номер 32).

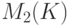Для коммутативного кольца обозначим через множество всех квадратных матриц порядка 2 с операциями сложения и умножения матриц. Как нетрудно видеть, мы получаем кольцо матриц над .

Теорема 6.3 Пусть 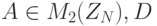- определитель матрицы . Следующие условия равносильны:

• ,
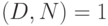• существует матрица, обратная к ,
• если хотя бы один из элементов 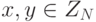отличен от нуля, то ,
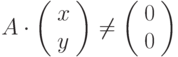• матрица задаёт взаимно однозначное отображение множества на себя.

На основании сформулированного утверждения мы можем выполнять шифрующее преобразование, используя матрицы из , у которых определители взаимно просты с .

Элемент открытого текста преобразуется в элемент шифртекста по правилу 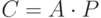, т.е.

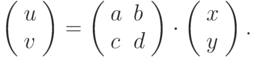
Расшифрование производится с помощью обратной матрицы: .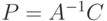

Пример 6.11 Зашифруем открытый текст ШИФРОВАНИЕ с помощью матрицы .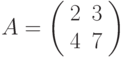

Биграмме ШИ соответствует вектор 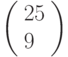, биграмме ФР - вектор 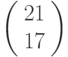, и так далее. Слову ШИФРОВАНИЕ соответствует последовательность векторов 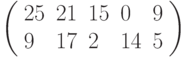. Умножаем их на шифрующую матрицу, выполняя вычисления по модулю 33:

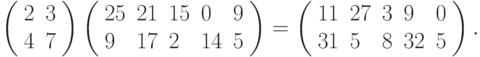
Теперь записываем биграммы, соответствующие полученным векторам: 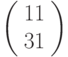соответствует КЮ, - ЪЕ, и так далее. Получаем шифртекст: КЮЪЕГЗИЯАЕ.

Шифрование триграмм проводится аналогично, триграмме сопоставляется вектор из трех компонент, а шифрующая матрица имеет порядок 3.