|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Алгоритмы тестирования на простоту и факторизации
2.1 Парадокс дней рождения
Теорема 2.3 Пусть 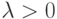 . Для случайной выборки объёма
. Для случайной выборки объёма  из
из  элементов, где
элементов, где 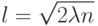 , вероятность
, вероятность  того, что все элементы выборки будут попарно различны, допускает следующую оценку сверху:
того, что все элементы выборки будут попарно различны, допускает следующую оценку сверху:
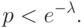
Следствие 2.1 (Парадокс дней рождения) Чтобы с вероятностью 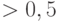 обнаружить двух людей, празднующих день рождения в один день, достаточно рассмотреть всего 23 человека.
обнаружить двух людей, празднующих день рождения в один день, достаточно рассмотреть всего 23 человека.
Этот парадокс допускает следующие применения в криптографии.
2.2.1 Алгоритм Полларда для факторизации натурального числа
Пусть нам требуется факторизовать натуральное число  , то есть найти любой его нетривиальный делитель. Один из простейших алгоритмов приведён ниже [1]. Алгоритм будет вычислять псевдослучайную последовательность
, то есть найти любой его нетривиальный делитель. Один из простейших алгоритмов приведён ниже [1]. Алгоритм будет вычислять псевдослучайную последовательность 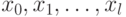 . Вероятность
. Вероятность  того, что
того, что 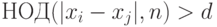 можно оценить по теореме 2.4. Если
можно оценить по теореме 2.4. Если  - минимальный делитель числа
- минимальный делитель числа  , то множество
, то множество 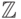 разбивается на
разбивается на  классов, причем если
классов, причем если  ,
, 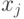 лежат в одном классе, то
лежат в одном классе, то 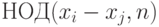 делится на
делится на  . Итак, в теореме 2.4 находим
. Итак, в теореме 2.4 находим 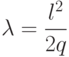 , и
, и  .
.
Если 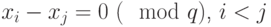 , а
, а 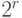 - наименьшая степень двойки, большая
- наименьшая степень двойки, большая  , то
, то 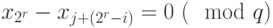 . Поэтому вместо того, чтобы сравнивать все пары
. Поэтому вместо того, чтобы сравнивать все пары  ,
, 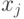 с произвольными
с произвольными 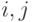 , имеет смысл сравнивать пары:
, имеет смысл сравнивать пары:
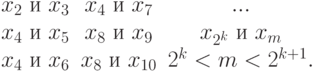
Для сравнения среди таких пар достаточно хранить 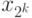 и
и 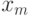 , тогда как для поиска среди всех пар нужно хранить все пары.
, тогда как для поиска среди всех пар нужно хранить все пары.
Правда, такая хитрость требует увеличить длину последовательности. Допустим, наименьшие  и
и  , для которых
, для которых 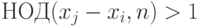 , равны, соответственно,
, равны, соответственно,  и
и  . Тогда
. Тогда
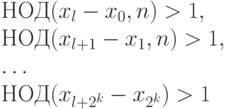
Поскольку мы сравниваем 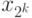 и
и 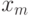 , где
, где 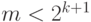 , то у нас
, то у нас 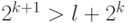 , то есть
, то есть  . Итак, нужно выбрать наименьшее
. Итак, нужно выбрать наименьшее  такое, что
такое, что  и вычислить не
и вычислить не  , а
, а 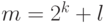 членов последовательности.
членов последовательности.
- Взять многочлен
 с целыми коэффициентами и случайное число
с целыми коэффициентами и случайное число  . Положить
. Положить 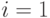 .
. - Вычислить
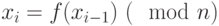 .
. - Если
 - степень двойки, положить
- степень двойки, положить  ,
, 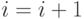 , перейти к предыдущему шагу.
, перейти к предыдущему шагу. - (Теперь
 - не степень двойки). Если
- не степень двойки). Если 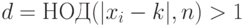 , то
, то  - нетривиальный делитель числа
- нетривиальный делитель числа  .
. - Положить
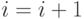 . Если
. Если  , перейти к шагу 2.
, перейти к шагу 2.
Отметим, что при фиксированном  длина
длина  вычисляемой последовательности пропорциональна
вычисляемой последовательности пропорциональна 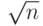 - верхней оценке наименьшего простого делителя
- верхней оценке наименьшего простого делителя  . Таким образом, данный алгоритм имеет сложность, экспоненциальную по числу бит числа
. Таким образом, данный алгоритм имеет сложность, экспоненциальную по числу бит числа  .
.
Пример 2.2 С помощью  -алгоритма Полларда найти нетривиальный простой делитель числа
-алгоритма Полларда найти нетривиальный простой делитель числа 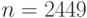 .
.
На первом шаге алгоритма требуется выбрать многочлен  для генерации последовательности
для генерации последовательности  . Возьмём
. Возьмём 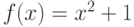 . Выберем длину
. Выберем длину  последовательности так, чтобы найти в ней повтор с вероятностью
последовательности так, чтобы найти в ней повтор с вероятностью 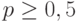 .
. 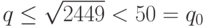 - оценка сверху для наименьшего простого делителя
- оценка сверху для наименьшего простого делителя  числа
числа  . Итак,
. Итак,  , откуда
, откуда 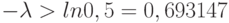 . Тогда
. Тогда
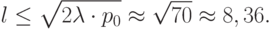
Допустим, в последовательности 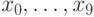 есть повтор. Чтобы гарантированно его найти с помощью приведённого алгоритма, нужно вычислить не меньше
есть повтор. Чтобы гарантированно его найти с помощью приведённого алгоритма, нужно вычислить не меньше 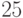 её членов. В самом деле, так как
её членов. В самом деле, так как  , то
, то  , и необходимое число членов:
, и необходимое число членов: 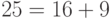 .
.
Выберем 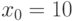 .
.
- Вычисляем
 ;
; - Вычисляем
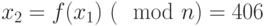 ; 2 - степень двойки; запоминаем
; 2 - степень двойки; запоминаем 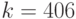 .
. - Вычисляем
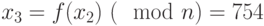 ,
, 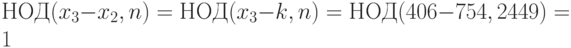 .
. - Вычисляем
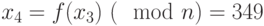 , 4 - степень двойки; запоминаем
, 4 - степень двойки; запоминаем 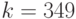 .
. - Вычисляем
 ,
, 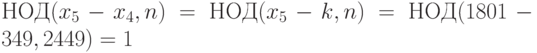 .
. - Вычисляем
 ,
,  .
. - Вычисляем
 ,
,  .
.
Итак, нам повезло найти нетривиальный делитель 31 числа 2449. Если бы мы досчитали до  и не нашли повтор, то нам лучше было бы выбрать новый
и не нашли повтор, то нам лучше было бы выбрать новый  (в качестве него можно взять
(в качестве него можно взять  ) и начать алгоритм сначала.
) и начать алгоритм сначала.
2.2.2 Алгоритм Полларда для дискретного логарифмирования
Изменим алгоритм предыдущего параграфа так, чтобы с его помощью решать задачу дискретного логарифмирования. Его идея остаётся прежней: мы будем вычислять последовательность 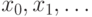 и будем находить среди них пары
и будем находить среди них пары  чисел. Зададим последовательность так, чтобы это равенство давало нам дискретный логарифм.
чисел. Зададим последовательность так, чтобы это равенство давало нам дискретный логарифм.
Найдём  из условия
из условия 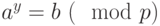 , где
, где  - простое число.
- простое число.
Определим последовательности 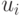 ,
,  ,
,  следующим образом:
следующим образом:
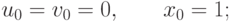
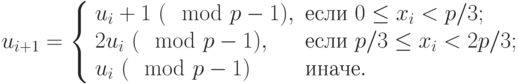
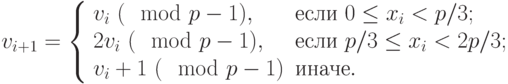
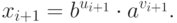
Тогда если  , то
, то  , откуда
, откуда
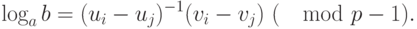
Коллизия  ищется тем же способом, что и в предыдущем параграфе.
ищется тем же способом, что и в предыдущем параграфе.
Отметим, что данный алгоритм может быть также обобщен для дискретного логарифмирования в произвольной циклической группе, и даже для поиска коллизий хэш-функций.

