| Россия |
Построение модели гибридных системы для обработки данных
Моделирование зависимости будем осуществлять с помощью следующей базы знаний:
- Если х1=СП и х2=ЕС и х3=УС, то у=10;
- Если х1=СП и х2=СЕС и х3=УС, то у=15;
- Если х1=СП и х2=НЕ и х3=УС, то у=20;
- Если х1=СП и х2=ЕС и х3=СУС, то у=20;
- Если х1=СП и х2=НЕ и х3=НУ, то у=40;
- Если х1=СРС и х2=ЕС и х3=УС, то у=15;
- Если х1=СРС и х2=СЕС и х3=УС , то у=20
- Если х1=СРС и х2= НЕ и х3= СУС, то у=60;
- Если х1=СРС и х2= ЕС и х3= НУ, то у=25
- Если х1=СРС и х2= СЕС и х3= СУС, то у=45
- Если х1=СРС и х2= НЕ и х3=НУ, то у=80
- Если х1=НР и х2= ЕС и х3= СУС, то у=25
- Если х1=НР и х2= ЕС и х3= УС, то у=15
- Если х1=НР и х2= СЕС и х3= СУС, то у=70
- Если х1=НР и х2= НЕ и х3= НУ, то у=100
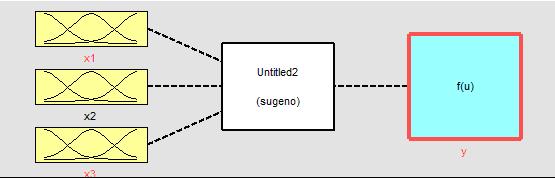
Для синтеза и исследования гибридной нейро-нечеткой системы управления потоком данных (Рисунок 14.6) использован инструмент MATLAB
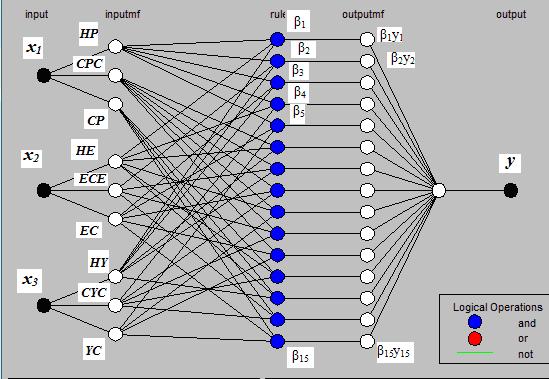
Любая нечеткая нейронная сеть работает как система нечеткого логического вывода, но строится не с помощью инженерных знаний, а с помощью обучения по образцам. В результате матрица весов отражает силу связи входных и выходных переменных. Результатом обучения служит не только матрица весов, но совокупность правил и оценок их достоверности (Рисунок 14.7).
Проектирование системы нечеткого логического вывода типа Сугэно состоит в выполнении следующей последовательности шагов. Сначала вводим три входных переменных и одну выходную. Обозначим входные переменные х1, х2, х3, а выходную переменную у. Обозначим термы и введем диапазон изменения переменных согласно выведенным правилам. Каждому терму будет соответствовать три переменные.
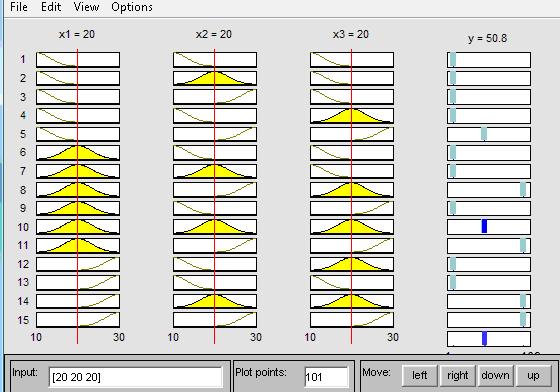
Текущее состояние системы описывается нечеткими тенденциями ее параметров (Рисунок 14.8).
Для формирования структуры гибридной нейро-нечеткой системы необходимо сформировать обучающую последовательность, записав ее в файл Test.data и передав этот файл инструменту anfisedit.
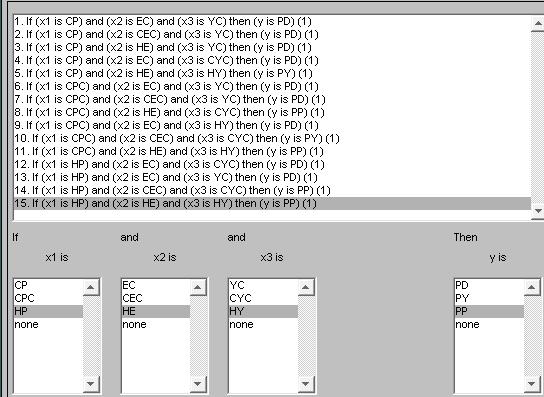
На основании полученной из файла обучающей последовательности инструмент anfisedit генерирует гибридную нейро-нечеткую систему со следующими характеристиками для входа 1 – СП, СРС, НП термов, для входа 2 – ЕС, CEC, HE термов, для входа 3 - YC,CYC,HY, для выхода – РD, PY, PP. Используя нечеткий логический вывод по алгоритму Сугэно, т.е. набор термов (см. Таблицу 14.1).
На основании построенного нечеткого алгоритма для системы Сугэно смоделируем гибридную нейронную сеть отображающую механизм вывода данной системы (Рисунок 14.9).
Структура данной сети может быть описана следующим образом.
Слой 1 (inputmf) Выходы узлов этого слоя представляют собой значения функции принадлежности при конкретных значения входов (х1, х2, х3), терм множества (x1?CP, CPC, HP; x2?EC, CEC, HE; x3?YC,CYC,HY).
Слой 2 (rule) Выходами нейронов этого слоя являются степени истинности предпосылок каждого правила базы знаний системы, вычисляемые по формулам:
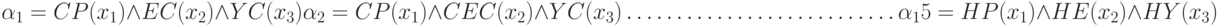 |
( 14.5) |
Все нейроны этого слоя реализовывают произвольную Т – норму для моделирования операции "И".
На этом этапе также рассчитывается и нормированная сила правила (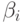 )
)
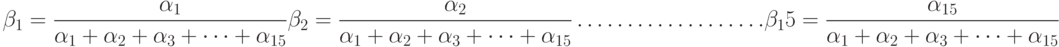 |
( 14.6) |
Слой 3 (outputmf) Формирует значения выходной переменной у (РР,PD,PY). Нейроны этого слоя выполняют следующие операции:
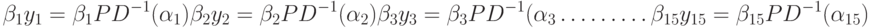 |
( 14.7) |
Слой 4 (output) Единственный нейрон этого слоя вычисляет выход сети:
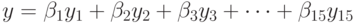 |
( 14.8) |
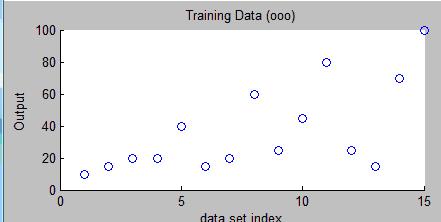
После загрузки данных получаем следующие результаты, изображенные на Рисунке 14.10.
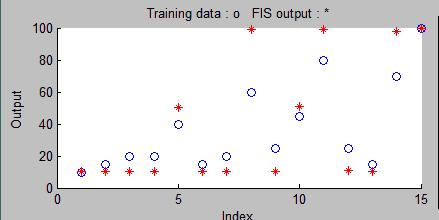
Протестируем систему. Как мы видим, система работает не вполне согласовано. Тестовые данные расходятся с данными при загрузке это четко видно из Рисунка 14.11 . Чтобы система работала согласно нашим данным, произведем обучение сети.